江西省南昌市2019年中考数学二模考试试卷

试卷更新日期：2020-04-26 类型：中考模拟

进入出卷网下载

一、单选题

1. $| - 2019 |$ 的值是（）

A、 $2019$ B、 $- 2019$ C、 $\frac{1}{2019}$ D、 $2019$ 或 $- 2019$

查看试题解析
2. 计算 ${(- 2 b)}^{3}$ 的结果是（）

A、 $8 b^{3}$ B、 $- 2 b^{3}$ C、 $- 8 b^{3}$ D、 $- 6 b^{3}$

查看试题解析
3. 李克强总理在2019年的政府工作报告中指出：三大攻坚战开局良好．其中精准脱贫有力推进，农村贫困人口减少1386万，易地扶贫搬迁280万人，数据1386万用科学记数法可表示为（）

A、 $1386 \times 10^{4}$ B、 $1.386 \times 10^{6}$ C、 $1.386 \times 10^{7}$ D、 $0.1386 \times 10^{8}$

查看试题解析
4. 第14届中国（深圳）国际茶产业博览会在深圳会展中心展出一只如图所示的茶杯（茶口的直径与托盘的直径相同），则这只茶杯的俯视图大致是（）

A、 B、 C、 D、

查看试题解析
5. 如图，在Rt△ABC中，∠ACB=90°，CD是∠ACB的平分线，交AB于点D ，过点D分别作AC、BC的平行线DE、DF ，则下列结论不正确是（）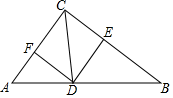

A、 $A D = B D$ B、 $F C = D F$ C、 $∠ A C D = ∠ B C D$ D、四边形DECF是正方形

查看试题解析
6. 如图， $P$ 是抛物线 $y = x^{2} - x - 4$ 在第四象限的一点，过点 $P$ 分别向 $x$ 轴和 $y$ 轴作垂线，垂足分别为 $A$ 、 $B$ ，则四边形 $O A P B$ 周长的最大值为（）

A、 $10$ B、 $8$ C、 $7.5$ D、 $5 \sqrt{3}$

查看试题解析

二、填空题

7. 分解因式：4x²–1= ．

查看试题解析
8. 已知关于x的一元二次方程x²+ax+b=0的两根分别为-1和2，则 $\frac{b}{2}$ = ．

查看试题解析
9. 如图，在Rt△ABC中，∠ACB=90°，AC=BC ，以AB为直径作⊙O ，在 $\overset{⌢}{A B C}$ 上取一点D ，使 $\overset{⌢}{B D}$ =2 $\overset{⌢}{A D}$ ，则∠CBD= ．

查看试题解析
10. 已知 $a$ ， $b$ ， $c$ 三个数的平均数是 $4$ ，且 $a$ ， $b$ ， $c$ ， $d$ 四个数的平均数是 $5$ ，则 $d$ 的值为．

查看试题解析
11. “今有木，不知长短，引绳度之，余绳四尺五寸，屈绳量之，不足一尺，木长几何”意思是：用一根绳子去量一根长木，绳子还剩余4.5尺，将绳子对折再量长木，长木还剩余1尺，则此木长是尺.

查看试题解析
12. 如图．反比例函数 $y = \frac{k}{x} (x > 0)$ 的图象与直线 $A B$ 交于点 $A (2 ， 3)$ ，直线 $A B$ 与 $x$ 轴交于点 $B (4 ， 0)$ ，过点 $B$ 作 $x$ 轴的垂线 $B C$ ，交反比例函数的图象于点 $C$ ，在平面内存在点 $D$ ，使得以 $A$ ， $B$ ， $C$ ， $D$ 四点为顶点的四边形为平行四边形，则点 $D$ 的坐标是．

查看试题解析

三、解答题

13.

(1)、解不等式：1- $\frac{x + 5}{2}$ ＜-1-x

(2)、解方程组： ${\begin{matrix} 4 x - y = 1 ① \\ x + y = 4 ② \end{matrix}$

查看试题解析
14. 如图，在 $▱ A B C D$ 中， $E$ 是 $B C$ 延长线上的一点， $A E$ 与 $C D$ 交于点 $F$ ．求证： $△ A D F \sim △ E B A$ ．

查看试题解析
15. 甲、乙两个工程队需完成A、B两个工地的工程．若甲、乙两个工程队分别可提供40个和50个标准工作量，完成A、B两个工地的工程分别需要70个和20个标准工作量，且两个工程队在A、B两个工地的1个标准工作量的成本如下表所示：

A工地

B工地

甲工程队

800元

750元

乙工程队

600元

570元

设甲工程队在A工地投入x（20≤x≤40）个标准工作量，完成这两个工程共需成本y元．

(1)、求y与x之间的函数关系式；

(2)、请判断y是否能等于62000，并说明理由．

查看试题解析
16. 如图，四边形 $A B C D$ 为菱形，且 $∠ B A D = 120 °$ ，以 $A D$ 为直径作 $⊙ O$ ，与 $C D$ 交于点 $P$ ．请仅用无刻度的直尺按下列要求画图．(保留作图痕迹)

(1)、在如图中，过点 $C$ 作 $A B$ 边上的高 $C E$ ．

(2)、在如图中，过点 $P$ 作 $⊙ O$ 的切线 $P Q$ ，与 $B C$ 交于点 $Q$ ．

查看试题解析
17. 举世瞩目的港珠澳大桥已于2018年10月24日正式通车，这座大桥是世界上最长的跨海大桥，被英国《卫报》誉为“新世界七大奇迹之一”当车辆经过这座大桥的收费站时，需从已开放的4个收费通道A、B、C、D中随机选择一个通过晶晶和贝贝两位同学的爸爸相约分别驾车经港珠澳大桥到香港旅行．

(1)、晶晶的爸爸驾车通过收费站时，选择A通道通过的概率是多少？

(2)、用画树状图或列表法求这两辆车经过此收费站时，选择不同通道通过的概率．

查看试题解析
18. 如图所示的是一个地球仪及它的平面图，在平面图中，点A、B分别为地球仪的南、北极点，直线AB与放置地球仪的平面交于点D ，所夹的角度约为67°，半径OC所在的直线与放置它的平面垂直，垂足为点E ， DE=15cm ， AD=14cm ．

(1)、求半径OA的长（结果精确到0.1cm ，参考数据：sin67°≈0.92，cos67°≈0.39，tan67°≈2.36）

(2)、求扇形BOC的面积（π取3.14，结果精确到1cm）

查看试题解析

19. 某居委会为了了解本辖区内家庭月平均用水情况，随机调查了该辖区内的部分家庭，调查数据统计结果如下：

月平均用水量x（吨）	频数	频率
0＜x≤5	6	0.12
5＜x≤10	a	0.24
10＜x≤15	16	0.32
15＜x≤20	10	0.20
20＜x≤25	4	0.08
25＜x≤30	2	0.04

请解答以下问题：

(1)、频数分布表中a= ，并把频数分布直方图补充完整；

(2)、求被调查的用水量不超过15吨的家庭占被调查家庭总数的百分比；

(3)、若该辖区内有1000户家庭，根据调查数据估计，该辖区月平均用水量超过20吨的家庭有多少户？

查看试题解析

20. 如图， $A B$ 是 $⊙ O$ 的直径，点 $C$ 、 $E$ 在 $⊙ O$ 上， $∠ B = 2 ∠ A C E$ ，在 $B A$ 的延长线上有一点 $P$ ，使得 $∠ P = ∠ B A C$ ，弦 $C E$ 交 $A B$ 于点 $F$ ，连接 $A E$ ．

(1)、求证： $P E$ 是 $⊙ O$ 的切线．

(2)、若 $A F = 2$ ， $A E = E F = \sqrt{10}$ ，求 $O A$ 的长．

查看试题解析
21. 如图，在平面直角坐标系中，一次函数 $y = a x + b (a \neq 0)$ 的图象与反比例函数 $y = \frac{k}{x} (k \neq 0)$ 的图象交于第一、三象限内的 $A$ 、 $B$ 两点，与 $y$ 轴交于 $C$ 点，过点 $A$ 作 $A M ⊥ x$ 轴于点 $M$ ，作 $A N ⊥ y$ 轴于点 $N$ ， $O M = 2$ ， $tan ∠ A O M = \frac{3}{2}$ ，点 $B$ 的坐标为 $(m ， - 2)$ ．

(1)、求四边形 $A M O N$ 的周长和面积．

(2)、求该反比例函数和一次函数的解析式．

查看试题解析
22. （操作发现）

(1)、如图1，将△ABC绕点A逆时针旋转90°得到△ADE ，连接BD ，则∠ABD的度数是．

(2)、（类比探究）
如图2，在等腰直角三角形ABC内取一点P ，使∠APB=135°，将△ABP绕顶点A逆时针旋转90°得到△ACP'，连接PP'．请猜想BP与CP'有怎样的位置关系，并说明理由．

(3)、（解决问题）
如图3，在等腰直角三角形ABC内任取一点P ，连接PA、PB、PC ．求证：PC+ $\sqrt{2}$ PA＞PB ．

查看试题解析
23. 我们规定，以二次函数y=ax²+bx+c的二次项系数a的2倍为一次项系数，一次项系数b为常数项构造的一次函数y=2ax+b叫做二次函数y=ax²+bx+c的“子函数”，反过来，二次函数y=ax²+bx+c叫做一次函数y=2ax+b的“母函数”．

(1)、若一次函数y=2x-4是二次函数y=ax²+bx+c的“子函数”，且二次函数经过点（3，0），求此二次函数的解析式及顶点坐标．

(2)、若“子函数”y=x-6的“母函数”的最小值为1，求“母函数”的函数表达式．

(3)、已知二次函数y=-x²-4x+8的“子函数”图象直线l与x轴、y轴交于C、D两点，动点P为二次函数y=-x²-4x+8对称轴右侧上的动点，求△PCD的面积的最大值．

查看试题解析

	A工地	B工地
甲工程队	800元	750元
乙工程队	600元	570元