江西省上饶市广丰区2019年中考数学一模考试试卷

试卷更新日期：2020-04-26 类型：中考模拟

进入出卷网下载

一、单选题

1. 在- $\frac{1}{2}$ 、- $\frac{1}{3}$ 、-|-2|、- $\sqrt{3}$ 这四个数中，最大的数是（）

A、 $- \frac{1}{2}$ B、 $- \frac{1}{3}$ C、 $- | - 2 |$ D、 $- \sqrt{3}$

查看试题解析
2. 下列运算正确是（）

A、 $a^{2} \cdot a^{4} = a^{8}$ B、 $2 a + 3 a = 5 a$ C、 $x (x - 2) = x^{2} - 2$ D、 $(x - 2) (x + 3) = x^{2} - 6$

查看试题解析
3. 已知不等式组 ${\begin{cases} x - 3 > 0 \\ x + 1 \geq 0 \end{cases}$ 其解集在数轴上表示正确是（）

A、 B、 C、 D、

查看试题解析
4. 我国古代数学著作《九章算术》中，将底面是直角三角形，且侧棱与底面垂直的三梭柱称为“堑堵”，已知“堑堵”的三视图如图所示(网格图中每个小正方形的边长均为1)，则该“堑堵”的体积为（）

A、 $16 + 16 \sqrt{2}$ B、 $16 + 8 \sqrt{2}$ C、 $24 + 16 \sqrt{2}$ D、16

查看试题解析
5. 如图，正六边形的中心为原点O，点A的坐标为(0，4)，顶点E(-1， $\sqrt{3}$ )，顶点B(1， $\sqrt{3}$ )，设直线AE与y轴的夹角∠EAO为α，现将这个六边形绕中心O旋转，则当α取最大角时，它的正切值为（）

A、 $\frac{1}{2}$ B、1 C、 $\frac{\sqrt{3}}{3}$ D、 $\frac{4 + \sqrt{3}}{13}$

查看试题解析
6. 已知抛物线y=-x²+2mx-m²+1与x轴的正半轴交于为A、B(点B在点A的右侧)，与y交于C，顶点为P．某数学学习小组在探究函数的图象与性质时得到以下结论：①开口向下，对称轴是直线x=m；②A(m-1，0)，B(m+1，0)；③函数最大值是1；④△BAP是等腰直角三角形；⑤当△BOC为等腰三角形时，抛物线的解析式是y=-x²+4x-3．以上结论正确有（）个．

A、1 B、2 C、3 D、4

查看试题解析

二、填空题

7. 计算：- $\sqrt[3]{- 8}$ ÷(-2)= ．

查看试题解析
8. 按照IMF的预测，中国的GDP的总值约为13.6万亿美元，13.6万亿美元用科学记数法可表示为美元．

查看试题解析
9. 5个正整数，中位数是4，唯一的众数是6，则这5个数和的最大值为．

查看试题解析
10. 对于任意实数 $a$ 、 $b$ ，定义： $a$ ◆ $b$ = $a^{2} + a b + b^{2}$ .若方程 $(x ◆ 2) - 6 = 0$ 的两根记为 $m$ 、 $n$ ，则m²+mn+n²=.

查看试题解析
11. 如图，已知菱形OABC的顶点O(0，0)，B(2，2)，若菱形绕点O逆时针旋转，每秒旋转45°，则第60秒时，菱形的顶点B的坐标为．

查看试题解析
12. 已知矩形OABC中，O为坐标原点，点A在x轴上，点C在y轴上，B的坐标为(10，5)，点P在边BC上，点A关于OP的对称点为A'，若点A'到直线BC的距离为4，则点A'的坐标可能为．

查看试题解析

三、解答题

13.

(1)、已知x满足x²-4x-2=0，求(2x-3)²-(x+y)(x-y)-y²的值；

(2)、如图，在等边△ABC中，点D、E分别在边BC、AC上，且DE∥AB，过点E作EF⊥DE，交BC的延长线于点F．求证：DC=CF．

查看试题解析
14. 已知关于x的分式方程 $\frac{2}{x - 1}$ + $\frac{mx}{(x - 1) (x + 2)}$ = $\frac{1}{x + 2}$ .

(1)、已知m=4，求方程的解；

(2)、若该分式方程无解，试求m的值．

查看试题解析
15. 如图，AB、AD是⊙O的弦，△ABC是等腰直角三角形，△ADC≌△AEB，请仅用无刻度直尺作图：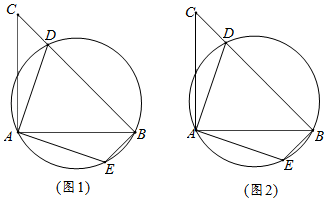

(1)、在图1中作出圆心O；

(2)、在图2中过点B作BF∥AC．

查看试题解析
16. 某校组织九年级学生参加中考体育测试，共租用4辆客车，分别编号为1、2、3、4．

(1)、求甲同学随机坐1号车的概率；

(2)、求甲、乙两位同学随机都乘坐1号车的概率．

查看试题解析
17. 小明通过“电e宝”查询得知电费分阶梯付费，如图：

(1)、已知小明家10月份累计电量为2060度，现“电e宝”短信通知11月交费177元，求小明家11份的用电量是多少度？

(2)、写出小明家12月的电费与年累计电量x度的关系式．

查看试题解析

18. 在创客教育理念的指引下，国内很多学校都纷纷建立创客实践室及创客空间，致力于从小培养孩子的创新精神和创造能力，某校开设了“3D”打印、数学编程、智能机器人、陶艺制作“四门创客课程记为A、B、C、D，为了解学生对这四门创客课程的喜爱情况，数学兴趣小组对全校学生进行了随机问卷调查，将调查结果整理后绘制成两幅均不完整的统计图表：

创客课程	频数	频率
“3D”打印	36	0.45
数学编程		0.25
智能机器人	16	b
陶艺制作	8
合计	a	1

请根据图表中提供的信息回答下列问题：

(1)、统计表中的a= ， b=；

(2)、“陶艺制作”对应扇形的圆心角为；

(3)、根据调查结果，请你估计该校300名学生中最喜欢“智能机器人”创客课程的人数；

(4)、学校为开设这四门课程，预计每生A、B、C、D四科投资比为4：3：6：7，若“3D打印课程每人投资200元，求学校为开设创客课程，需为学生人均投入多少钱？

查看试题解析

19. 如图，在平面直角坐标系中，矩形OBDC的两边OB、OC分别在x轴和y轴上，点D在反比例函数y= $\frac{8}{x}$ 的图象上，反比例函数y= $\frac{k}{x}$ 的图象交DC、BD于点E、F．

(1)、若CE：DC=1：4，求k的值；

(2)、连接BC、EF，求证：EF∥BC．

查看试题解析
20. 如图，甲、乙两车在行驶、超车过程均近似地看作直线平移，已知甲、乙两车均以20米/秒的速度在右车道匀速行驶，甲车头D与乙车头A之间的距离AD=50米，车宽EC=1.8米，为保证安全，一般车子在行驶过程中与车行道分界线相距0.6米，甲、乙两车行驶路线与CD所在直线平行于道路分界线，现乙车加速，沿路线AB加速行驶到左车道，且∠BAC=1.5^o ，若B、C、E刚好在同一水平线上．

(1)、求CD的距离；

(2)、已知该高速路段限速110km/h，判断乙车在超车过程是否超速？请通过计算说明．
(参考数据：tanl.5^o≈0.015，sin1.5^o≈0.014)

查看试题解析
21. 如图，点E为正方形ABCD边AB上运动，点A与点F关于DE对称，作射线CF交DE延长线于点P，连接AP、BF．

(1)、若∠ADE=15°，求∠DPC的度数；

(2)、试探究AP与PC的位置关系，并说明理由；

(3)、若AB=2，求BF的最小值．

查看试题解析

22. 某数学兴趣小组在探究函数y=|x²-4x+3|的图象和性质时，经历以下几个学习过程：

(1)、列表(完成以下表格)

x	…	-2	-1	0	1	2	3	4	5	6	…
y₁=x²-4x+3	…	15	8		0		0	3		15	…
y=\|x²-4x+3\|	…	15	8		0		0	3		15	…

(2)、描点并画出函数图象草图(在备用图1中描点并画图)

(3)、根据图象完成以下问题

(ⅰ)观察图象

函数y=|x²-4x+3|的图象可由函数y₁=x²-4x+3的图象如何变化得到？

答：．

(ⅱ)数学小组探究发现直线y=8与函数y=|x²-4x+3|的图象交于点E、F，E(-1，8)，F(5，8)，则不等式|x²-4x+3|＞8的解集是；

(4)、设函数y=|x²-4x+3|的图象与x轴交于A、B两点(B位于A的右侧)，与y轴交于点C．

①求直线BC的解析式；

②探究应用：将直线BC沿y轴平移m个单位后与函数y=|x²-4x+3|的图象恰好有3个交点，求此时m的值．

查看试题解析

23. 如图， $E ， F$ 分别为 $△ A B C$ 中 $A C ， A B$ 上的动点（点 $A 、 B 、 C$ 除外），连接 $E B ， F C$ 交于点P， $B C = 6$ .我们约定：线段 $B C$ 所对的 $∠ C P B$ ，称为线段 $B C$ 的张角.

情景发现

(1)、已知三角形 $A B C$ 是等边三角形， $A E = B F$ ，
①求线段 $B C$ 的张角 $∠ C P B$ 的度数；

②求点P到 $B C$ 的最大距离；

③若点P的运动路线的长度称为点P的路径长，求点P的路径长.

拓展探究

(2)、在（1）中，已知 $△ A^{'} B C$ 是圆P的外切三角形，若点 $A^{'}$ 的运动路线的长度称为点 $A^{'}$ 的路径长，试探究点 $A^{'}$ 的路径长与点P的路径长之间有何关系？请通过计算说明.

查看试题解析