北京市东城区2016-2017学年高考文数二模考试试卷

试卷更新日期：2017-09-12 类型：高考模拟

进入出卷网下载

一、选择题

1. 已知全集U是实数集R．如图的韦恩图表示集合M={x|x＞2}与N={x|1＜x＜3}关系，那么阴影部分所表示的集合可能为（）

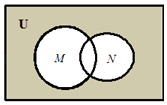A、{x|x＜2} B、{x|1＜x＜2} C、{x|x＞3} D、{x|x≤1}

查看试题解析
2. 已知向量 $\vec{a}$ =（1，2）， $\vec{b}$ =（x，4），且 $\vec{a}$ ⊥ $\vec{b}$ ，那么x的值为（）

A、﹣2 B、﹣4 C、﹣8 D、﹣16

查看试题解析
3. 下列函数既是奇函数，又在区间[﹣1，1]上单调递减的是（）

A、f（x）=sinx B、f（x）=|x+1| C、f（x）=﹣x D、f（x）=cosx

查看试题解析
4. 在平面直角坐标系中，不等式组 ${\begin{matrix} x \geq 0 \\ x + y \leq 2 \\ x \leq y \end{matrix}$ 所表示的平面区域的面积为（）

A、1 B、2 C、4 D、8

查看试题解析
5. 已知x，y∈R，那么“x＞y”的充分必要条件是（）

A、2^x＞2^y B、lgx＞lgy C、 $\frac{1}{x} > \frac{1}{y}$ D、x²＞y²

查看试题解析
6. 已知直线x+y=m（m＞0）与圆x²+y²=1相交于P，Q两点，且∠POQ=120°（其中O为原点），那么m的值是（）

A、 $\frac{\sqrt{3}}{3}$ B、 $\frac{\sqrt{2}}{2}$ C、 $\sqrt{2}$ D、 $\sqrt{3}$

查看试题解析
7. 日晷，是中国古代利用日影测得时刻的一种计时工具，又称“日规”．其原理就是利用太阳的投影方向来测定并划分时刻．利用日晷计时的方法是人类在天文计时领域的重大发明，这项发明被人类沿用达几千年之久．如图是故宫中的一个日晷，则根据图片判断此日晷的侧（左）视图可能为（）

A、 B、 C、 D、

查看试题解析
8. 已知甲、乙两个容器，甲容器容量为x，装满纯酒精，乙容器容量为z，其中装有体积为y的水（x，y＜z，单位：L）．现将甲容器中的液体倒入乙容器中，直至甲容器中液体倒完或乙容器盛满，搅拌使乙容器中两种液体充分混合，再将乙容器中的液体倒入甲容器中直至倒满，搅拌使甲容器中液体充分混合，如此称为一次操作，假设操作过程中溶液体积变化忽略不计．设经过n（n∈N^*）次操作之后，乙容器中含有纯酒精a_n（单位：L），下列关于数，列{a_n}的说法正确的是（）

A、当x=y=a时，数列{a_n}有最大值 $\frac{a}{2}$ B、设b_n=a_n+1﹣a_n（n∈N^*），则数列{b_n}为递减数列 C、对任意的n∈N^* ，始终有 $a_{n} \leq \frac{x y}{z}$ D、对任意的n∈N^* ，都有 $a_{n} \leq \frac{x y}{x + y}$

查看试题解析

二、填空题

9. 已知△ABC三内角A，B，C对应的边长分别为a，b，c，且 $B = \frac{2 π}{3}$ ，又边长b=3c，那么sinC= ．

查看试题解析
10. 已知 $\frac{1}{1 + i} = \frac{1}{2}$ ﹣ni其中n是实数，i是虚数单位，那么n= ．

查看试题解析
11. 如图茎叶图记录了甲，乙两班各六名同学一周的课外阅读时间（单位：小时），已知甲班数据的平均数为13，乙班数据的中位数为17，那么x的位置应填；y的位置应填．

查看试题解析
12. 已知函数f（x）=1nx+2x﹣6的零点在区间（ $\frac{k}{2}$ ， $\frac{k + 1}{2}$ ）（k∈Z）内，那么k= ．

查看试题解析
13. 已知双曲线G以原点O为中心，过 $(\sqrt{5} ， 4)$ 点，且以抛物线C：y²=4x的焦点为右顶点，那么双曲线G的方程为．

查看试题解析
14. 如图，在棱长为2的正方体ABCD﹣A₁B₁C₁D₁中，E为对角线B₁D上的一点，M，N为对角线AC上的两个动点，且线段MN的长度为1．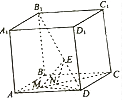
⑴当N为对角线AC的中点且DE= $\sqrt{2}$ 时，则三棱锥E﹣DMN的体积是；
⑵当三棱锥E﹣DMN的体积为 $\frac{1}{3}$ 时，则DE= ．

查看试题解析

三、解答题

15. 在等差数列{a_n}中，a₁=﹣2，a₁₂=20．
（Ⅰ）求通项a_n；
（Ⅱ）若 $b_{n} = \frac{a_{1} + a_{2} + \dots a_{n}}{n}$ ，求数列 ${3^{b_{n}}}$ 的前n项和．

查看试题解析
16. 函数 $f (x) = A s i n (ω x + \frac{π}{6}) (A > 0 ， ω > 0)$ 的最大值为2，它的最小正周期为2π．
（Ⅰ）求函数f（x）的解析式；
（Ⅱ）若g（x）=cosx•f（x），求g（x）在区间 $[- \frac{π}{6} ， \frac{π}{4}]$ 上的最大值和最小值．

查看试题解析
17. 某单位附近只有甲，乙两个临时停车场，它们各有50个车位，为了方便市民停车，某互联网停车公司对这两个停车场在工作日某些固定时刻的剩余停车位进行记录，如下表：
时间
8点
10点
12点
14点
16点
18点
停车场甲
10
3
12
6
12
17
停车场乙
13
4
3
2
6
19
如果表中某一时刻停车场剩余停车位数低于总车位数的10%，那么当车主驱车抵达单位附近时，该公司将会向车主发出停车场饱和警报．
（Ⅰ）假设某车主在以上六个时刻抵达单位附近的可能性相同，求他收到甲停车场饱和警报的概率；
（Ⅱ）从这六个时刻中任选一个时刻，求甲停车场比乙停车场剩余车位数少的概率；
（Ⅲ）当停车场乙发出饱和警报时，求停车场甲也发出饱和警报的概率．

查看试题解析
18. 如图，在四棱柱ABCD﹣A₁B₁C₁D₁中，侧面ADD₁A₁和侧面CDD₁C₁都是矩形，BC∥AD，△ABD是边长为2的正三角形，E，F分别为AD，A₁D₁的中点．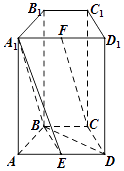
（Ⅰ）求证：DD₁⊥平面ABCD；
（Ⅱ）求证：平面A₁BE⊥平面ADD₁A₁；
（Ⅲ）若CF∥平面A₁BE，求棱BC的长度．

查看试题解析
19. 设函数f（x）=（x﹣a）•e^x ， a∈R．
（Ⅰ）当a=1时，试求f（x）的单调增区间；
（Ⅱ）试求f（x）在[1，2]上的最大值；
（Ⅲ）当a=1时，求证：对于∀x∈[﹣5，+∞）， $f (x) + x + 5 \geq - \frac{6}{e^{5}}$ 恒成立．

查看试题解析
20. 已知椭圆E：mx²+y²=1（m＞0）．
（Ⅰ）若椭圆E的右焦点坐标为 $(\sqrt{3} ， 0)$ ，求m的值；
（Ⅱ）由椭圆E上不同三点构成的三角形称为椭圆的内接三角形．若以B（0，1）为直角顶点的椭圆E的内接等腰直角三角形恰有三个，求m的取值范围．

查看试题解析

时间	8点	10点	12点	14点	16点	18点
停车场甲	10	3	12	6	12	17
停车场乙	13	4	3	2	6	19