安徽省芜湖市2016-2017学年高考文数5月份模拟考试试卷
试卷更新日期:2017-09-12 类型:高考模拟
一、选择题:
-
1. 设复数z满足(1﹣i)z=|1+ |(i为虚数单位),则 在复平面内对应的点位于( )A、第一象限 B、第二象限 C、第三象限 D、第四象限2. 已知全集U=Z,A={x∈Z|x2﹣x﹣2≥0},B={﹣1,0,1,2},则(∁UA)∩B=( )A、{﹣1,2} B、{﹣1,0} C、{0,1} D、{1,2}3. 若﹣1<sinα+cosα<0,则( )A、sinα<0 B、cosα<0 C、tanα<0 D、cos2α<04. 已知点 在双曲线 的一条浙近线上,则a=( )A、 B、3 C、2 D、5. “a2=1”是“函数 为奇函数”的( )A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件6. 执行所给的程序框图,则输出的值是( )
 A、 B、 C、 D、7. 边长为4的正三角形ABC中,点D在边AB上, = ,M是BC的中点,则 • =( )A、16 B、 C、 D、﹣88. 等比数列{an}共有2n+1项,其中a1=1,偶数项和为170,奇数项和为341,则n=( )A、3 B、4 C、7 D、99. 函数f(x)=x2•cosx在 的图象大致是( )A、
A、 B、 C、 D、7. 边长为4的正三角形ABC中,点D在边AB上, = ,M是BC的中点,则 • =( )A、16 B、 C、 D、﹣88. 等比数列{an}共有2n+1项,其中a1=1,偶数项和为170,奇数项和为341,则n=( )A、3 B、4 C、7 D、99. 函数f(x)=x2•cosx在 的图象大致是( )A、 B、
B、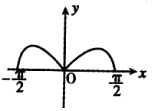 C、
C、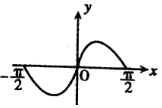 D、
D、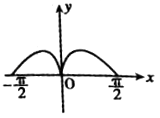 10. 抛物线x2=4y的焦点为F,过F作斜率为 的直线l与抛物线在y轴右侧的部分相交于点A,过A作抛物线准线的垂线,垂足为H,则△AHF的面积是( )A、4 B、 C、 D、811. 将函数f(x)=sinωx(ω>0)的图象向左平移 个单位得到函数g(x)的图象,若函数g(x)的图象关于直线x=ω对称且在区间(﹣ω,ω)内单调递增,则ω的值为( )A、 B、 C、 D、12. 若函数f(x)= 有最大值,则实数a的取值范围是( )A、 B、 C、[﹣2,+∞) D、
10. 抛物线x2=4y的焦点为F,过F作斜率为 的直线l与抛物线在y轴右侧的部分相交于点A,过A作抛物线准线的垂线,垂足为H,则△AHF的面积是( )A、4 B、 C、 D、811. 将函数f(x)=sinωx(ω>0)的图象向左平移 个单位得到函数g(x)的图象,若函数g(x)的图象关于直线x=ω对称且在区间(﹣ω,ω)内单调递增,则ω的值为( )A、 B、 C、 D、12. 若函数f(x)= 有最大值,则实数a的取值范围是( )A、 B、 C、[﹣2,+∞) D、二、填空题
-
13. 下茎叶图记录了某学习小组六名同学在一次数学测试中的成绩(单位:分),已知该组数据的中位数为85,则x的值为 .
 14. 如图,网格纸上的小正方形边长为1,粗线画出的是某几何体的三视图,则该几何体外接球的体积为 .
14. 如图,网格纸上的小正方形边长为1,粗线画出的是某几何体的三视图,则该几何体外接球的体积为 . 15. 已知点P(x,y)在不等式组 (a为常数)表示的平面区域上运动,若z=4x+3y的最大值为8,则a= .16. 在△ABC中,角A,B,C所对的边分别为a,b,c,且bcosC=(3a﹣c)cosB.D为AC边的中点,且BD=1,则△ABD面积的最大值为 .
15. 已知点P(x,y)在不等式组 (a为常数)表示的平面区域上运动,若z=4x+3y的最大值为8,则a= .16. 在△ABC中,角A,B,C所对的边分别为a,b,c,且bcosC=(3a﹣c)cosB.D为AC边的中点,且BD=1,则△ABD面积的最大值为 .三、解答题
-
17. 设等差数列{an}的前n项和为Sn , 若S9=81,a3+a5=14.(1)、求数列{an}的通项公式;(2)、设bn= ,若{bn}的前n项和为Tn , 证明:Tn< .18. 2017年3月14日,“ofo共享单车”终于来到芜湖,ofo共享单车又被亲切称作“小黄车”是全球第一个无桩共享单车平台,开创了首个“单车共享”模式.相关部门准备对该项目进行考核,考核的硬性指标是:市民对该项目的满意指数不低于0.8,否则该项目需进行整改,该部门为了了解市民对该项目的满意程度,随机访问了使用共享单车的100名市民,并根据这100名市民对该项目满意程度的评分,绘制了如下频率分布直方图:

(I)为了了解部分市民对“共享单车”评分较低的原因,该部门从评分低于60分的市民中随机抽取2人进行座谈,求这2人评分恰好都在[50,60)的概率;
(II)根据你所学的统计知识,判断该项目能否通过考核,并说明理由.
(注:满意指数= )
19. 如图所示,在直角梯形ABCD中,AD∥BC,AD⊥DC,BC=2AD=2DC,四边形ABEF是正方形,且平面ABEF⊥平面ABCD,M为AF的中点,(I)求证:AC⊥BM;
(II)求异面直线CE与BM所成角的余弦值.
 20. 已知椭圆C: 的离心率为 ,M为C上除长轴顶点外的一动点,以M为圆心, 为半径作圆,过原点O作圆M的两条切线,A、B为切点,当M为短轴顶点时∠AOB= .
20. 已知椭圆C: 的离心率为 ,M为C上除长轴顶点外的一动点,以M为圆心, 为半径作圆,过原点O作圆M的两条切线,A、B为切点,当M为短轴顶点时∠AOB= .(Ⅰ)求椭圆的方程;
(Ⅱ)设椭圆的右焦点为F,过点F作MF的垂线交直线x= a于N点,判断直线MN与椭圆的位置关系.
21. 已知函数f(x)=(ax﹣1)lnx+ .(Ⅰ)若a=2,求曲线y=f(x)在点(1,f(1))处的切线l的方程;
(Ⅱ)设函数g(x)=f'(x)有两个极值点x1 , x2 , 其中x1∈(0,e),求g(x1)﹣g(x2)的最小值.