安徽省马鞍山市2016-2017学年高考文数三模考试试卷

试卷更新日期：2017-09-12 类型：高考模拟

进入出卷网下载

一、选择题

1. 已知集合A={x|（x﹣3）（x+1）≤0}，B={x|﹣2＜x≤2}，则A∩B=（）

A、[﹣2，﹣1] B、[﹣1，2] C、[﹣1，1] D、[1，2]

查看试题解析
2. 设i为虚数单位，则复数 $z = \frac{1 - i}{1 + i}$ 的模为（）

A、1 B、 $\sqrt{2}$ C、 $\sqrt{3}$ D、2

查看试题解析
3. “α=2kπ﹣ $\frac{π}{4}$ （k∈Z）”是“cosα= $\frac{\sqrt{2}}{2}$ ”的（）

A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件

查看试题解析
4. 已知双曲线 $\frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} = 1$ （a＞0，b＞0）的离心率为2，则该双曲线的渐近线方程为（）

A、x±y=0 B、 $x \pm \sqrt{3} y = 0$ C、 $\sqrt{3} x \pm y = 0$ D、2x±y=0

查看试题解析
5. 《九章算术》“勾股”章有一题：“今有二人同立．甲行率七，乙行率三，乙东行，甲南行十步而斜东北与乙会，问甲乙各行几何？”大意是说：“已知甲、乙二人同时从同一地点出发，甲的速度为7，乙的速度为3，乙一直向东走，甲先向南走10步，后又斜向北偏东方向走了一段后与乙相遇．甲、乙各走了多少步？”请问乙走的步数是（）

A、 $\frac{9}{2}$ B、 $\frac{15}{2}$ C、 $\frac{21}{2}$ D、 $\frac{49}{2}$

查看试题解析
6. 执行如图的程序框图，若输出的 $S = \frac{31}{32}$ ，则输入的整数p的值为（）

A、6 B、5 C、4 D、3

查看试题解析
7. 已知函数f（x）=cos（2x﹣ $\frac{π}{6}$ ）+sin2x，则f（x）的一个单调递减区间是（）

A、[﹣ $\frac{π}{3}$ ， $\frac{π}{6}$ ] B、[﹣ $\frac{π}{3}$ ， $\frac{2 π}{3}$ ] C、[﹣ $\frac{π}{6}$ ， $\frac{5 π}{6}$ ] D、[ $\frac{π}{6}$ ， $\frac{2 π}{3}$ ]

查看试题解析
8. 函数f（x）的定义域为R，若f（x+1）与f（x﹣1）都是奇函数，则f（5）=（）

A、﹣1 B、0 C、1 D、5

查看试题解析
9. 已知椭圆E： $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (a > b > 0)$ 的右焦点为F（3，0），过点F的直线交椭圆E于A、B两点．若AB的中点坐标为（1，﹣1），则E的方程为（）

A、 $\frac{x^{2}}{45} + \frac{y^{2}}{36} = 1$ B、 $\frac{x^{2}}{36} + \frac{y^{2}}{27} = 1$ C、 $\frac{x^{2}}{27} + \frac{y^{2}}{18} = 1$ D、 $\frac{x^{2}}{18} + \frac{y^{2}}{9} = 1$

查看试题解析
10. 已知实数x，y满足 ${\begin{matrix} x + y \geq 1 \\ m x - y \leq 0 \\ 2 x - y + 2 \geq 0 \end{matrix}$ ，若z=3x﹣y的最大值为1，则m的值为（）

A、 $\frac{8}{3}$ B、2 C、1 D、 $\frac{2}{3}$

查看试题解析
11. 已知△ABC的顶点都在半径为R的球O的球面上，球心O到平面ABC的距离为 $\frac{\sqrt{3}}{2} R$ ， $A B = B C = A C = \sqrt{3}$ ，则球O的体积是（）

A、 $\frac{16}{3} π$ B、16π C、 $\frac{32}{3} π$ D、32π

查看试题解析
12. 已知函数f（x）= ${\begin{matrix} l n x ， x > 0 \\ \frac{m}{x} ， x < 0 \end{matrix}$ ，若f（x）﹣f（﹣x）=0有四个不同的根，则m的取值范围是（）

A、（0，2e） B、（0，e） C、（0，1） D、（0， $\frac{1}{e}$ ）

查看试题解析

二、填空题

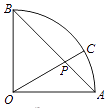
13. 已知向量 $\vec{a}$ =（2，1）， $\vec{b}$ =（x，﹣1），若 $\vec{a}$ ∥（ $\vec{a}$ ﹣ $\vec{b}$ ），则 $\vec{a} \cdot \vec{b}$ = ．

查看试题解析
14. 如图，扇形AOB的圆心角为90°，点P在弦AB上，且OP= $\sqrt{2}$ AP，延长OP交弧AB于点C，现向该扇形内随机投一点，则该点落在扇形AOC内的概率为．

查看试题解析
15. 某几何体的三视图如图所示，则该几何体的体积为

查看试题解析
16. 在锐角△ABC中，内角A，B，C的对边分别为a，b，c，且（c+b）（sinC﹣sinB）=a（sinA﹣sinB）．若c=2 $\sqrt{3}$ ，则a²+b²的取值范围是．

查看试题解析

三、解答题：

17. 已知数列{a_n}的前n项和为S_n ，且2S_n=4a_n﹣1．
（Ⅰ）求{a_n}的通项公式；
（Ⅱ）设b_n=a_n•a_n+1﹣2，求数列{b_n}的前n项和T_n ．

查看试题解析
18. 2017年3月27日，一则“清华大学要求从2017级学生开始，游泳达到一定标准才能毕业”的消息在体育界和教育界引起了巨大反响．游泳作为一项重要的求生技能和运动项目受到很多人的喜爱．其实，已有不少高校将游泳列为必修内容．某中学为了解2017届高三学生的性别和喜爱游泳是否有关，对100名高三学生进行了问卷调查，得到如下列联表：
喜欢游泳
不喜欢游泳
合计
男生
10
女生
20
合计
已知在这100人中随机抽取1人，抽到喜欢游泳的学生的概率为 $\frac{3}{5}$ ．
（Ⅰ）请将上述列联表补充完整；
（Ⅱ）判断是否有99.9%的把握认为喜欢游泳与性别有关？
附： $K^{2} = \frac{n {(a d - b c)}^{2}}{(a + b) (c + d) (a + c) (b + d)}$
p（K²≥k₀）
0.10
0.05
0.025
0.010
0.005
0.001
k₀
2.706
3.841
5.024
6.635
7.879
10.828

查看试题解析
19. 已知几何体ABCDEF中，AB∥CD，AD⊥DC，EA⊥平面ABCD，FC∥EA，AB=AD=EA=1，CD=CF=2．
（Ⅰ）求证：平面EBD⊥平面BCF；
（Ⅱ）求点B到平面ECD的距离．

查看试题解析
20. 已知曲线C：y²=4x，M：（x﹣1）²+y²=4（x≥1），直线l与曲线C相交于A、B两点，O为坐标原点．
（Ⅰ）若 $\vec{O A} \cdot \vec{O B} = - 4$ ，求证：直线l恒过定点，并求出定点坐标；
（Ⅱ）若直线l与曲线C₁相切，M（1，0），求 $\vec{M A} \cdot \vec{M B}$ 的取值范围．

查看试题解析
21. 已知函数f（x）=（x﹣1）lnx﹣（x﹣a）²（a∈R）．
（Ⅰ）若f（x）在（0，+∞）上单调递减，求a的取值范围；
（Ⅱ）若f（x）有两个极值点x₁ ， x₂ ，求证：x₁+x₂＞ $\frac{5}{4}$ ．

查看试题解析
22. 已知曲线C₁的参数方程为 ${\begin{matrix} x = 1 + \frac{1}{2} t \\ y = \frac{\sqrt{3}}{2} t \end{matrix}$ （为参数）．在以坐标原点为极点，轴的正半轴为极轴的极坐标系中，曲线C₂： $ρ^{2} = \frac{12}{3 + s i n^{2} θ}$ ．
（Ⅰ）求曲线C₁的普通方程和C₂的直角坐标方程；
（Ⅱ）若C₁与C₂相交于A、B两点，设点F（1，0），求 $\frac{1}{| F A |} + \frac{1}{| F B |}$ 的值．

查看试题解析
23. 设函数f（x）=|x﹣a|+|2x+2|﹣5（a∈R）．
（Ⅰ）试比较f（﹣1）与f（a）的大小；
（Ⅱ）当a=﹣5时，求函数f（x）的图象与轴围成的图形面积．

查看试题解析

p（K²≥k₀）	0.10	0.05	0.025	0.010	0.005	0.001
k₀	2.706	3.841	5.024	6.635	7.879	10.828

	喜欢游泳	不喜欢游泳	合计
男生		10
女生	20
合计