初中数学浙教版八年级下册5.3 正方形(2) 同步训练
试卷更新日期:2020-04-24 类型:同步测试
一、基础夯实
-
1. 正方形具有而菱形不一定具有的性质是( ).A、四条边都相等 B、对角线互相垂直且平分 C、对角线相等 D、对角线平分一组对角2. 如图,是由三个边长分别为6、9、x的正方形所组成的图形,若直线AB将它分成面积相等的两部分,则x的值是( ).
 A、4或6 B、3或5 C、1或7 D、3或63. 如图,矩形内有两个相邻的正方形,其面积分别为2和8,则图中阴影部分的面积为( )
A、4或6 B、3或5 C、1或7 D、3或63. 如图,矩形内有两个相邻的正方形,其面积分别为2和8,则图中阴影部分的面积为( )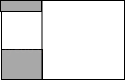 A、 B、2 C、 D、64. 如图,四张大小不一的正方形纸片分别放置于矩形的四个角落,其中,①和②纸片既不重叠也无空隙.在矩形ABCD的周长已知的情况下,知道下列哪个正方形的边长,就可以求得阴影部分的周长( )
A、 B、2 C、 D、64. 如图,四张大小不一的正方形纸片分别放置于矩形的四个角落,其中,①和②纸片既不重叠也无空隙.在矩形ABCD的周长已知的情况下,知道下列哪个正方形的边长,就可以求得阴影部分的周长( )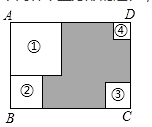 A、① B、② C、③ D、④5. 如图1,分别沿长方形纸片ABCD和正方形纸片EFGH的对角线AC,EG剪开,拼成如图2所示的▱ALMN,若中间空白部分四边形OPQR恰好是正方形,且▱ALMN的面积为50,则正方形EFGH的面积为( )
A、① B、② C、③ D、④5. 如图1,分别沿长方形纸片ABCD和正方形纸片EFGH的对角线AC,EG剪开,拼成如图2所示的▱ALMN,若中间空白部分四边形OPQR恰好是正方形,且▱ALMN的面积为50,则正方形EFGH的面积为( )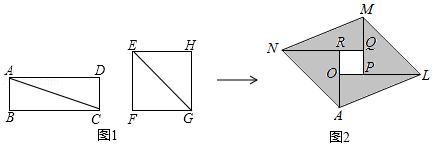 A、24 B、25 C、26 D、276. 如果正方形的对角线长为 ,那么这个正方形的面积为.7. 如图,点E在正方形ABCD的边BA的延长线上,连接AC,AC=AE,CE交AD于点F,则∠ACE的度数等于.
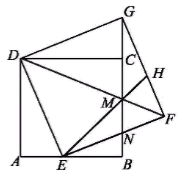
A、24 B、25 C、26 D、276. 如果正方形的对角线长为 ,那么这个正方形的面积为.7. 如图,点E在正方形ABCD的边BA的延长线上,连接AC,AC=AE,CE交AD于点F,则∠ACE的度数等于. 8. 如图,正方形ABCD的对角线AC,BD相交于点O.E,G分别是OB,OC上的点,CE与DG的延长线相交于点F.若DF⊥CE,求证:OG=OE.
8. 如图,正方形ABCD的对角线AC,BD相交于点O.E,G分别是OB,OC上的点,CE与DG的延长线相交于点F.若DF⊥CE,求证:OG=OE.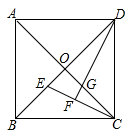 9. 如图,已知正方形ABCD的边长为1,正方形CEFG的面积为S1 , 点E在DC边上,点G在BC的延长线上,设以线段AD和DE为邻边的矩形的面积为 S2 , 且S1=S2.
9. 如图,已知正方形ABCD的边长为1,正方形CEFG的面积为S1 , 点E在DC边上,点G在BC的延长线上,设以线段AD和DE为邻边的矩形的面积为 S2 , 且S1=S2. (1)、求线段CE的长.(2)、若点日为BC边的中点,连接HD,求证:HD=HG.
(1)、求线段CE的长.(2)、若点日为BC边的中点,连接HD,求证:HD=HG.二、提高特训
-
10. 如图,四边形ABCD是正方形,直线L1、L2、L3 , 若L1与L2的距离为5,L2与L3的距离7,则正方形ABCD的面积等于( )
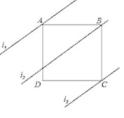 A、70 B、74 C、144 D、14811. 如图,正方形ABCD的边长为2,P为CD的中点,连结AP,过点B作BE⊥AP于点E,延长CE交AD于点F,过点C作CH⊥BE于点G,交AB于点H,连接HF。下列结论正确的是( )
A、70 B、74 C、144 D、14811. 如图,正方形ABCD的边长为2,P为CD的中点,连结AP,过点B作BE⊥AP于点E,延长CE交AD于点F,过点C作CH⊥BE于点G,交AB于点H,连接HF。下列结论正确的是( )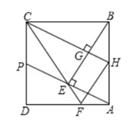 A、CE= B、EF= C、cos∠CEP= D、HF2=EF·CF12. 如图,将n个边长都为2的正方形按如图所示摆放,点A1、A2、A3 , …,An分别是正方形的中心,则这n个正方形重叠的面积之和是( )
A、CE= B、EF= C、cos∠CEP= D、HF2=EF·CF12. 如图,将n个边长都为2的正方形按如图所示摆放,点A1、A2、A3 , …,An分别是正方形的中心,则这n个正方形重叠的面积之和是( )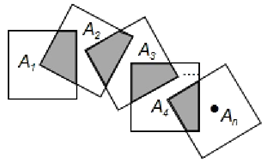 A、n B、n-1 C、4n D、4(n-1)
A、n B、n-1 C、4n D、4(n-1)