初中数学浙教版八年级下册5.2 菱形（2） 同步训练
试卷更新日期：2020-04-24 类型：同步测试
一、基础夯实
-
1. 如图在△ABC中，DE∥BC，EF∥AB，要判定四边形DBFE是菱形，还需要添加的条件是（ ）
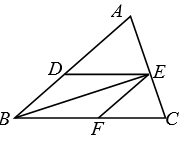A、AB=AC B、AD=BD C、BE⊥AC D、BE平分∠ABC2. 如图，矩形A BCD的对角线AC，BD相交于点O，CE//BD，DE//AC.若AC=4，则四边形CODE的周长是（ ）.
A、4 B、6 C、8 D、103. 已知四边形ABCD中， ，对角线AC，BD相交于点O.下列结论一定成立的是（ ）A、 B、 C、 D、4. 如图，由10根完全相同的小棒拼接而成，请你再添2根与前面完全相同的小棒，拼接后的图形恰好有3个菱形的方法共有（ ）
A、3种 B、4种 C、5种 D、6种5. 下列条件中，能判断四边形是菱形的是（ ）A、对角线互相垂直且相等的四边形 B、对角线互相垂直的四边形 C、对角线相等的平行四边形 D、对角线互相平分且垂直的四边形6. 如图，CD与BE互相垂直平分，AD⊥DB，∠BDE=70°，则∠CAD=°．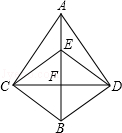
7. 如图，已知四边形ABCD为平行四边形，对角线AC，BD相交于点O，要使四边形ABCD为菱形，需要增加的一个条件是：.（只填一个你认为正确的条件即可，不添加任何线段与字母）
8. 如图，小聪在作线段AB的垂直平分线时，他是这样操作的：分别以A和B为圆心，大于 的长为半径画弧，两弧相交于C，D，则直线CD即为所求．根据他的作图方法可知四边形ACBD一定是 ．
9. 两个完全相同的矩形纸片ABCD、BFDE如图放置，AB＝BF.求证：四边形BNDM为菱形.
10. 如图，在平行四边形ABCD中，已知AD＞AB．
(1)、实践与操作：作∠BAD的平分线交BC于点E，在AD上截取AF=AB，连接EF；（要求：尺规作图，保留作图痕迹，不写作法）(2)、猜想并证明：猜想四边形ABEF的形状，并给予证明．二、提高特训
-
11. 如图，在给定的一张平行四边形纸片上按如下操作：连结 ，作 的垂直平分线 分别交 ， ， 于 ， ， ，连结 ， ，则四边形 是（ ）
A、菱形 B、矩形 C、正方形 D、无法判断12. 如图，是一张平行四边形纸片ABCD，要求利用所学知识作出一个菱形，甲、乙两位同学的作法分别如下：甲：连接AC，作AC的中垂线交AD、BC于E、F，则四边形AFCE是菱形.
乙：分别作 ∠A 与 ∠B 的平分线AE、BF，分别交BC于点E，交AD于点F，则四边形ABEF是菱形.
对于甲、乙两人的作法，可判断（ ）
A、甲正确，乙错误 B、甲错误，乙正确 C、甲、乙均正确 D、甲、乙均错误13. 如图，已知△ABC，∠ACB＝90°，BC＝3，AC＝4，小红按如下步骤作图：①分别以A、C为圆心，以大于 AC的长为半径在AC两边作弧，交于两点M、N；②连接MN，分别交AB、AC于点D、O；③过C作CE∥AB交MN于点E，连接AE、CD．则四边形ADCE的周长为（ ）
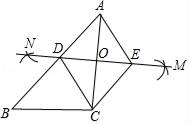A、10 B、20 C、12 D、2414. 如图，在 中，点 ， 分别是 ， 的中点，连接 ， ， ，且 ，过点 作 交 的延长线于点 .
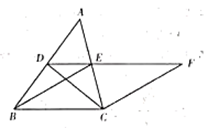(1)、求证：四边形 是菱形；(2)、在不添加任何辅助线和字母的情况下，请直接写出图中与 面积相等的所有三角形（不包括 ）.15. 如图，等腰△ABC中，已知AC＝BC＝2 ， AB＝4，作∠ACB的外角平分线CF，点E从点B沿着射线BA以每秒2个单位的速度运动，过点E作BC的平行线交CF于点F．
(1)、求证：四边形BCFE是平行四边形；(2)、当点E是边AB的中点时，连接AF，试判断四边形AECF的形状，并说明理由；(3)、设运动时间为t秒，是否存在t的值，使得以△EFC的其中两边为邻边所构造的平行四边形恰好是菱形？不存在的，试说明理由；存在的，请直接写出t的值．答：t＝ ．