初中数学浙教版八年级下册5.1 矩形(2) 同步训练
试卷更新日期:2020-04-24 类型:同步测试
一、基础夯实
-
1. 在数学活动课上,老师要求同学们判断一个四边形的门框是否为矩形,下面是某合作学习小组的四位同学拟定的方案,其中正确的是( )A、测量对角线是否相互平分 B、测量两组对边是否分别相等 C、测量一组对角线是否垂直 D、测量其内角是否有三个直角2. 若顺次连接四边形ABCD各边的中点所得四边形是矩形,则四边形ABCD一定是( )A、矩形 B、菱形 C、对角线相等的四边形 D、对角线互相垂直的四边形3. 四边形ABCD的对角线互相平分,要使它变为矩形,需要添加的条件是( )A、AB=CD B、AB=BC C、AC⊥BD D、AC=BD4. 如图,连接四边形ABCD各边的中点得到四边形EFGH,要使四边形EFGH为矩形,则对角线AC、BD应满足( )
 A、AC= BD B、AC平分BD C、AC= BD且AC⊥BD D、AC⊥BD5. 如图,四边形ABCD的对角线AC,BD相交于点O,已知下列6个条件:①AB∥DC;②AB=DC;③AC=BD;④∠ABC=90°;⑤OA=OC;⑥OB=OD.则不能使四边形ABCD成为矩形的是( )
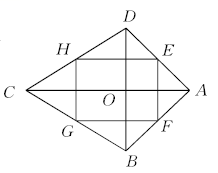
A、AC= BD B、AC平分BD C、AC= BD且AC⊥BD D、AC⊥BD5. 如图,四边形ABCD的对角线AC,BD相交于点O,已知下列6个条件:①AB∥DC;②AB=DC;③AC=BD;④∠ABC=90°;⑤OA=OC;⑥OB=OD.则不能使四边形ABCD成为矩形的是( )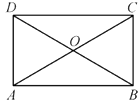 A、①②③ B、②③④ C、②⑤⑥ D、④⑤⑥6. 如图,四边形ABCD中,对角线相交于点O,E,F,G,H分别是AD,BD,BC,AC的中点,要使四边形EFGH是矩形,则四边形ABCD需要满足的条件是
A、①②③ B、②③④ C、②⑤⑥ D、④⑤⑥6. 如图,四边形ABCD中,对角线相交于点O,E,F,G,H分别是AD,BD,BC,AC的中点,要使四边形EFGH是矩形,则四边形ABCD需要满足的条件是 A、 B、 C、 D、7. 如图△ABC中,AC的垂直平分线分别交AC,AB于点D,F,BE⊥DF交DF的延长线于点E,已知∠A=30°,BC=2,AF=BF,则四边形BCDE的面积是( )
A、 B、 C、 D、7. 如图△ABC中,AC的垂直平分线分别交AC,AB于点D,F,BE⊥DF交DF的延长线于点E,已知∠A=30°,BC=2,AF=BF,则四边形BCDE的面积是( ) A、2 B、3 C、4 D、48. 在四边形ABCD中,AD∥BC,∠D=90°,如果再添加一个条件,可以得到四边形ABCD是矩形,那么可以添加的条件是: . (不再添加线或字母,写出一种情况即可)9. 如图,菱形ABCD的对角线AC、BD相交于点O,过点D、C分别作AC、BD的平行线,交于点E.
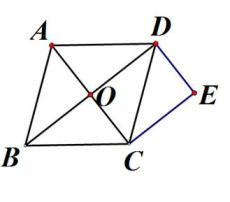
A、2 B、3 C、4 D、48. 在四边形ABCD中,AD∥BC,∠D=90°,如果再添加一个条件,可以得到四边形ABCD是矩形,那么可以添加的条件是: . (不再添加线或字母,写出一种情况即可)9. 如图,菱形ABCD的对角线AC、BD相交于点O,过点D、C分别作AC、BD的平行线,交于点E.求证:四边形ODEC为矩形;
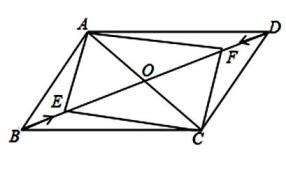
 10. 如图,△ABC中,D是BC边上一点,E是AD的中点,过点A作BC的平行线交BE的延长线于F,且AF=CD,连接CF.
10. 如图,△ABC中,D是BC边上一点,E是AD的中点,过点A作BC的平行线交BE的延长线于F,且AF=CD,连接CF. (1)、求证:△AEF≌△DEB;(2)、若AB=AC,试判断四边形ADCF的形状,并证明你的结论.
(1)、求证:△AEF≌△DEB;(2)、若AB=AC,试判断四边形ADCF的形状,并证明你的结论.二、提高特训
-
11. 如图所示,将矩形ABCD的四个角向内折起,恰好拼成一个既无缝又无重叠的四边形EFGH,若EH=3,EF=4,那么线段AD与AB的比等于( )
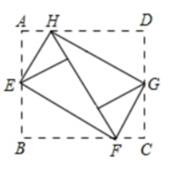 A、25:24 B、16:15 C、5:4 D、4:312. 如图,在矩形ABCD中,BC=20cm,点P和点Q分别从点B和点D出发,按逆时针方向沿矩形ABCD的边运动,点P和点Q的速度分别为3cm/s和2cm/s,则最快s后,四边形ABPQ成为矩形.
A、25:24 B、16:15 C、5:4 D、4:312. 如图,在矩形ABCD中,BC=20cm,点P和点Q分别从点B和点D出发,按逆时针方向沿矩形ABCD的边运动,点P和点Q的速度分别为3cm/s和2cm/s,则最快s后,四边形ABPQ成为矩形.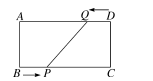 13. 如图,在Rt△ABC中,∠C=90°,AC=6,BC=8,P为AB边上不与A,B重合的一动点,过点P分别作PE⊥AC于点E,PF⊥BC于点F,则线段EF的最小值是 .
13. 如图,在Rt△ABC中,∠C=90°,AC=6,BC=8,P为AB边上不与A,B重合的一动点,过点P分别作PE⊥AC于点E,PF⊥BC于点F,则线段EF的最小值是 .