2015年福建省厦门市中考数学真题试卷

试卷更新日期：2016-04-21 类型：中考真卷

进入出卷网下载

一、单选题

1. 反比例函数y= $\frac{1}{x}$ 的图象是（　　）

A、线段 B、直线 C、抛物线 D、双曲线

查看试题解析
2. 一枚质地均匀的骰子，骰子的六个面上分别刻有1到6的点数，投掷这样的骰子一次，向上一面点数是偶数的结果有（　　）

A、1种 B、2种 C、3种 D、6种

查看试题解析
3. 已知一个单项式的系数是2，次数是3，则这个单项式可以是（　　）

A、﹣2xy² B、3x² C、2xy³ D、2x³

查看试题解析
4.
如图，△ABC是锐角三角形，过点C作CD⊥AB，垂足为D，则点C到直线AB的距离是（　　）

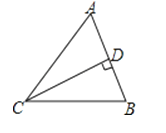A、线段CA的长 B、线段CD的长 C、线段AD的长 D、线段AB的长

查看试题解析
5. 2^﹣³可以表示为（　　）

A、2²÷2⁵ B、2⁵÷2² C、2²×2⁵ D、（﹣2）×（﹣2）×（﹣2）

查看试题解析
6.
如图，在△ABC中，∠C=90°，点D，E分别在边AC，AB上．若∠B=∠ADE，则下列结论正确的是（　　）

A、∠A和∠B互为补角 B、∠B和∠ADE互为补角 C、∠A和∠ADE互为余角 D、∠AED和∠DEB互为余角

查看试题解析
7. 某商店举办促销活动，促销的方法是将原价x元的衣服以（ $\frac{4}{5}$ x﹣10）元出售，则下列说法中，能正确表达该商店促销方法的是（　　）

A、原价减去10元后再打8折 B、原价打8折后再减去10元 C、原价减去10元后再打2折 D、原价打2折后再减去10元

查看试题解析
8. 已知sin6°=a，sin36°=b，则sin²6°=（　　）

A、a² B、2a C、b² D、b

查看试题解析
9.
如图，某个函数的图象由线段AB和BC组成，其中点A（0， $\frac{4}{3}$ ），B（1， $\frac{1}{2}$ ），C（2， $\frac{5}{3}$ ），则此函数的最小值是（　　）

A、0 B、 $\frac{1}{2}$ C、1 D、 $\frac{5}{3}$

查看试题解析
10.
如图，在△ABC中，AB=AC，D是边BC的中点，一个圆过点A，交边AB于点E，且与BC相切于点D，则该圆的圆心是（　　）

A、线段AE的中垂线与线段AC的中垂线的交点 B、线段AB的中垂线与线段AC的中垂线的交点 C、线段AE的中垂线与线段BC的中垂线的交点 D、线段AB的中垂线与线段BC的中垂线的交点

查看试题解析

二、填空题

11. 不透明的袋子里装有1个红球，1个白球，这些球除颜色外无其他差别，从袋子中随机摸出一个球，则摸出红球的概率是 .

查看试题解析
12. 方程x²+x=0的解是　 .

查看试题解析
13.
已知A，B，C三地位置如图所示，∠C=90°，A，C两地的距离是4km，B，C两地的距离是3km，则A，B两地的距离是 km；若A地在C地的正东方向，则B地在C地的方向.

查看试题解析
14.
如图，在矩形ABCD中，对角线AC，BD相交于点O，E是边AD的中点．若AC=10，DC= $2 \sqrt{5}$ ，则BO= ，∠EBD的大小约为　度分．（参考数据：tan26°34′≈ $\frac{1}{2}$ ）

查看试题解析
15. 已知（39+ $\frac{8}{13}$ ）×（40+ $\frac{9}{13}$ ）=a+b，若a是整数，1＜b＜2，则a= .

查看试题解析
16. 已知一组数据1，2，3，…，n（从左往右数，第1个数是1，第2个数是2，第3个数是3，依此类推，第n个数是n）．设这组数据的各数之和是s，中位数是k，则s= （用只含有k的代数式表示）．

查看试题解析

三、解答题

17. 计算：1﹣2+2×（﹣3）² ．

查看试题解析
18.
在平面直角坐标系中，已知点A（﹣3，1），B（﹣2，0），C（0，1），请在图中画出△ABC，并画出与△ABC关于原点O对称的图形．

查看试题解析
19. 计算： $\frac{x}{x + 1}$ + $\frac{x + 2}{x + 1}$ ．

查看试题解析
20.
如图，在△ABC中，点D，E分别在边AB，AC上，若DE∥BC，AD=3，AB=5，求 $\frac{D E}{B C}$ 的值．

查看试题解析
21. 解不等式组 $\{\begin{matrix} 2 x > 2 \\ x + 2 \leq 6 + 3 x \end{matrix}$

查看试题解析
22. 某公司欲招聘一名工作人员，对甲、乙两位应聘者进行面试和笔试，他们的成绩（百分制）如表所示．
应聘者
面试
笔试
甲
87
90
乙
91
82
若公司分别赋予面试成绩和笔试成绩6和4的权，计算甲、乙两人各自的平均成绩，谁将被录取？

查看试题解析
23.
如图，在△ABC中，AB=AC，点E，F分别是边AB，AC的中点，点D在边BC上．若DE=DF，AD=2，BC=6，求四边形AEDF的周长．

查看试题解析
24. 已知实数a，b满足a﹣b=1，a²﹣ab+2＞0，当1≤x≤2时，函数y= $\frac{a}{x}$ （a≠0）的最大值与最小值之差是1，求a的值．

查看试题解析
25.
如图，在平面直角坐标系中，点A（2，n），B（m，n）（m＞2），D（p，q）（q＜n），点B，D在直线y= $\frac{1}{2}$ x+1上．四边形ABCD的对角线AC，BD相交于点E，且AB∥CD，CD=4，BE=DE，△AEB的面积是2．
求证：四边形ABCD是矩形．

查看试题解析

四、综合题

26. 已知点A（﹣2，n）在抛物线y=x²+bx+c上．

(1)、若b=1，c=3，求n的值；

(2)、若此抛物线经过点B（4，n），且二次函数y=x²+bx+c的最小值是﹣4，请画出点P（x﹣1，x²+bx+c）的纵坐标随横坐标变化的图象，并说明理由．

查看试题解析
27. 已知四边形ABCD内接于⊙O，∠ADC=90°，∠DCB＜90°，对角线AC平分∠DCB，延长DA，CB相交于点E．

(1)、
如图1，EB=AD，求证：△ABE是等腰直角三角形；

(2)、
如图2，连接OE，过点E作直线EF，使得∠OEF=30°，当∠ACE≥30°时，判断直线EF与⊙O的位置关系，并说明理由．

查看试题解析

应聘者	面试	笔试
甲	87	90
乙	91	82