江苏省兴化市2019-2020学年八年级上学期数学期末考试试卷
试卷更新日期：2020-04-23 类型：期末考试
一、选择题(本大题共有6小题，每小题3分，共18分)
-
1. 下列交通标志中，轴对称图形的是（ ）A、
B、
C、
D、
2. 下列调查适合做普查的是（ ）A、了解全球人类男女比例情况 B、了解一批灯泡的平均使用寿命 C、调查20~25岁年轻人最崇拜的偶像 D、对确诊新冠肺炎患者同一车厢的乘客进行检查3. 下列说法中，错误的是 （ ）A、平行四边形的对角线互相平分 B、矩形的对角线互相垂直 C、菱形的对角线互相垂直平分 D、正方形的对角线相等4. 为了了解2019年秋学期兴化市八年级学生学业水平考试的数学成绩，从中随机抽取了700名学生的数学成绩。下列说法正确的是（ ）A、2019年秋学期兴化市八年级学生的全体是总体 B、每一名八年级学生是个体 C、从中抽取的700名八年级学生的数学成绩是总体的一个样本 D、样本容量是700名5. 如图，矩形ABCD中，∠AOB=60°，AB=2，则AC的长为（ ）
A、4 B、2 C、 D、6. 如图，直角三角形纸片中，直角边BC=8cm，AC=6cm，现将直角边AC沿直线AD折叠，使它落在斜边AB上，且与AE重合，则CD等于（ ）
A、2cm B、3cm C、4cm D、5cm二、填空题(本大题共有10小题，每小题3分，共30分)
-
7. “从超市货架上任意取一盒月饼进行检验，结果合格”这一事件是(填“必然事件”“不可能事件”“随机事件”).8. 函数y= 中，自变量x的取值范围是 ．9. 小芳掷一枚质地均匀的硬币，正面向上的概率为。10. 如果一个直角二角形的两条直角边的长分别是5和12，那么这个直角三角形斜边长是。11. 如图是七年级(1)班参加课外兴趣小组人数的扇形统计图，则表示唱歌兴趣小组人数的扇形的圆心角度数是。
12. 等腰三角形的腰AB=10，底边BC=12，则△ABC的周长为。13. 已知菱形ABCD的对角线相交于点O，AC=8cm，BD=6m，则菱形的面积为cm2。
14. 已知y与x-3成正比例，当x=4时，y=3，则y与x之间的函数表达式为 。15. 如果四边形的两条对角线长分别为35cm和25cm，则连接这个四边形各边中点所得的四边形的周长是cm。16. 如图，正方形ABCD的边长是4，∠DAC的平分线交DC于点E，若点P、Q分别是AD和AE上的动点，则DQ+PQ的最小值是 。
三、解答题(本大题共有8小题，共72分)
-
17. 求出下列x的值：(1)、4x2-16=0；(2)、3(x+1)3=2418. 5只不透明的袋子中各装有10个球，每个球除颜色外都相同。
(1)、将球搅匀，分别从每只袋子中摸一个球，摸到白球的概率一样大吗？为什么？(2)、将袋子的序号按摸到白球的概率从小到大的顺序排列。19. 如图，在平行四边形ABCD中，E、F分别是AB、CD上的点，且AE=CF。求证：DE=BF。
20. 为了加强学生课外阅读，开阔视野，某校开展了“书香校园，从我做起”的主题活动，学校随机抽取了部分学生，对他们一周的课外阅读时间进行调查，绘制出频数分布表和频数分布直方图的一部分如下：课外阅读时间(单位：小时)
频数(人数)
频数
0<t≤2
2
0.04
2<t≤4
3
0.06
4<t≤6
15
0.30
6<t≤8
a
0.50
t>8
5
b
请根据图表信息回答下列问题：
(1)、频数分布表中的a= ， b=；(2)、将频数分布直方图补充完整；(3)、学校将每周课外阅读时间在8小时以上的学生评为“阅读之星”，请你估计该校2000名学生中评为“阅读之星”的有多少人？21. 已知直线l1：y=3x-3和直线l2：y= x+6相交于点A。(1)、求点A坐标；(2)、若l1与x轴交于点B，l2与x轴交于点C，求△ABC面积。22. 如图，在△ABC中，点O是AC边上的一动点，过点O作直线MN∥BC，MN交∠BCA的平分线于点E，交∠BCA的外角平分线于点F。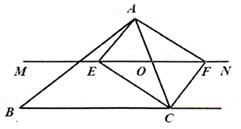
(1)、求证：EO=FO；(2)、当点O运动到何处时，四边形AECF是矩形？证明你的结论；(3)、当点O运动到何处时，且△ABC具备什么条件时，四边形AECF是正方形？试说明理由。23. 如图，平面直角坐标系中，CB∥OA，∠OCB=90°，CB=2，OC=4，直线y= x+2过A点，且与y轴交于D点。
(1)、求点A、点B的坐标；(2)、试说明：AD⊥BO；(3)、若点M是直线AD上的一个动点，在x轴上是否存在另一个点N，使以O、B、M、N为顶点的四边形是平行四边形？若存在，请直接写出点N的坐标；若不存在，请说明理由。24. 如图
(1)、如图1，在四边形ABCD中，AB=CD，E、F分别是BC、AD的中点，连接EF并延长，分别与BA、CD的延长线交于点M、N，证明：∠BME=∠CNE。请将证明∠BME=∠CNE的过程填写完整：
证明：连接BD，取BD的中点H，连接HE、HF。
∵F是AD的中点，H是BD的中点，
∴HF∥ ， HF= ， 同理：HE∥ ， HE= ，
∴∠1=∠BME，∠2=∠CNE，
又∵AB=CD，∴HF=HE，∴∠1=∠2，∴∠BME=∠CNE
(2)、运用上题方法解决下列问题：问题一：如图2，在四边形ADBC中，AB与CD相交于点O，AB=CD，E、F分别是BC、AD的中点，连接EF， 分别交DC、AB于点M、N，请判断△OMN的形状，并说明理由；
问题二：如图3，在钝角△ABC中，AC>AB，D点在AC上，E、F分别是BC、AD的中点，连接EF并延长，与BA的延长线交于点G，连接GD，若∠EFC=60°，△AGD是直角三角形且∠AGD=90°，求证：AB=CD。