湖北省武汉市青山区2020年中考数学四调模拟试卷（三）
试卷更新日期：2020-04-23 类型：中考模拟
一、选择题(共10小题，每小题3分，共30分)
-
1. 的值是（ ）A、2 B、4 C、6 D、82. 若分式 有意义，则x的取值范围是（ ）A、x≠5 B、x≠-5 C、x>5 D、x>-53. 下列计算正确的是（ ）A、2a2+a2=3a4 B、a2·a3=a6 C、(-a)4÷(-a)²=a² D、(a²)3=a54. 下列事件是必然事件的是（ ）A、抛掷一枚硬币四次，有两次正面朝上 B、打开电视频道，正在播放《奔跑吧，兄弟》 C、射击运动员射击一次，命中十环 D、方程x²-2x-1=0必有实数根5. 计算(x-3)(3+x)的结果为（ ）A、3-x² B、9+x2 C、x²-9 D、3+x26. 如图，已知 ABCD三个顶点坐标是A(-1，0) 、B(-2，-3) 、C(2，-1) ，那么第四个顶点D的坐标是（ ）
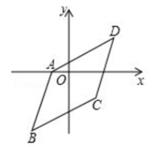A、(3，1) B、(3，2) C、(3，3) D、(3，4)7. 一个空心的圆柱如图，那么它的左视图是（ ）
A、
B、
C、
D、
8. 某校田径队10名队员的年龄分布如下表：年龄(岁)
13
14
15
16
人数
4
3
2
1
则这10名队员年龄的众数和中位数分别是（ ）
A、13和13 B、13和14 C、14和14 D、13和13.59. 正方形A1B1C1O、A2B2C2C1、A3B3C3C2 ， …按如图的方式放置，A1、A2、A3、…和点C1、C2、C3 ， …分别在直线y=x+1和x轴上，则点B6的坐标是（ ）
A、(63，32) B、(64，32) C、(32，16) D、(128，64)10. 如图，半径为2cm，圆心角为90°的扇形OAB的弧AB上有一运动的点P，从点P向半径OA引垂线PH交OA于点H。设△OPH的内心为I，当点P在弧AB上从点A运动到点B时，内心I所经过的路径长为（ ）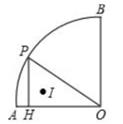
A、 B、 C、 D、π二、填空题(本大题共6个小题，每小题3分，共18分)
-
11. 计算：-17-(-2)=。12. =。13. “服务社会，提升自我．”凉山州某学校积极开展志愿者服务活动，来自九年级的5名同学(三男两女)成立了“交通秩序维护”小分队。若从该小分队任选两名同学进行交通秩序维护，则恰是一男一女的概率是。14. 如图，矩形ABCD将△DEC沿DE折叠得到△DC1E。若DC1平分∠ADE，则∠BEC1的度数是。
15. 如图，在正方形ABCD中，P为AB的中点，BE⊥PD的延长线于点E，连接AE、BE、FA⊥AE交DP于点F，连接BF，FC。若AE=2，则FC=。
16. 抛物线y=2x²-8x+6与x轴交于点A、B，把抛物线在x轴及其下方的部分记为C1 ， 将C1向右平移得到C2 ， C2与x轴交于点B、D，若直线y=-x+m与C1、C2共有3个不同的交点，则m的取值范围是。
三、解答题(共8题，共72分)
-
17. 解方程：2-2(x-1)=3x+418. 如图，Rt△ABC和Rt△DEF中，∠C=∠F=90°，AB=DE，CE=FB，求证：∠A=∠D。
19. 某校检测学生跳绳水平，抽样调查了部分学生的“1分钟跳绳”成绩，并制成了下面的频数分布直方图(每小组含最小值，不含最大值)和扇形图。
(1)、D组的人数是人，补全频数分布直方图，扇形图中m=；(2)、本次调查数据中的中位数落在组；(3)、如果“1分钟跳绳”成绩大于或等于120次为优秀，那么该校4500名学生中“1分钟跳绳”成绩为优秀的大约有多少人？20. 2016年5月6日，中国第一条具有自主知识产权的长沙磁浮线正式开通运营，该路线连接了长沙火车南站和黄花国际机场两大交通枢纽，沿线生态绿化带走廊的建设尚在进行中，届时将给乘客带来美的享受．星城渣土运输公司承包了某标段的土方运输任务，拟派出大、小两种型号的渣土运输车运输土方，已知2辆大型渣土运输车与3辆小型渣土运输车一次共运输土方31吨，5辆大型渣土运输车与6辆小型渣土运输车一次共运输土方70吨．(1)、一辆大型渣土运输车和一辆小型渣土运输车一次各运输土方多少吨？(2)、该渣土运输公司决定派出大、小两种型号的渣土运输车共20辆参与运输土方，若每次运输土方总量不少于148吨，且小型渣土运输车至少派出2辆，则有哪几种派车方案？21. 如图，AB为⊙O的直径，C为⊙O上一点，AD和过点C的切线互相垂直，垂足为D。
(1)、求证：AC平分∠DAB；(2)、若sin∠ABC= ，求tan∠BDC的值。22. 已知：A(a，y1)，B(2a，y2)是反比例函数y= (k>0)图象上的两点。
(1)、比较y1与y2的大小关系；(2)、若A、B两点在一次函数y= x+b第一象限的图象上(如图所示)，分别过A、B两点作x轴的垂线，垂足分别为C、D，连接OA、OB，且S△OAB=8，求a的值；(3)、在(2)的条件下，如果3m=-4x+24，3n= ，求使得m>n的x的取值范围。23. 如图，点E是矩形ABCD的边BC的中点，连接DE交AC于点F。
(1)、如图①，求证：AF=2CF；(2)、如图②，作DG上AC于G，试探究：当AB与AD满足什么关系时，使得AG=CF成立？并证明你的结论；(3)、如图③，以DE为斜边在矩形ABCD内部作等腰Rt△DEM，交对角线BD于N，连接AM，若AB=AD，请直接写出 的值。24. 如图，在平面直角坐标系xOy中，一次函数y= x+m(m为常数) 的图象与x轴交于点A(-3，0)，与y轴交于点C，以直线x=1为对称轴的拋物线y=ax2+bx+c(a、b、c为常数，且a≠0)经过A、C两点，并与x轴的正半轴交于点B。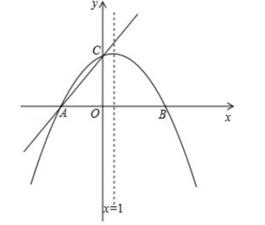
(参考公式：在平面直角坐标之中，若A((x1 ， y1)，B(x2 ， y2)，则A，B两点间的距离为AB= )
(1)、求m的值及抛物线的函数表达式；(2)、是否存在抛物线上一动点Q， 使得△ACQ是以AC为直角边的直角三角形？若存在， 求出点Ｑ的横坐标；若存在，请说明理由；(3)、若P是抛物线对称轴上一动点， 且使△ACP周长最小， 过点P任意作一条与y轴不平行的直线交抛物线于M1 (x1 ， y1)，M2(x2；y2)两点，试问 是否为定值，如果是，请求出结果，如果不是请说明理由。