湖北省武汉市青山区2020年中考数学四调模拟试卷(二)
试卷更新日期:2020-04-23 类型:中考模拟
一、选择题(共10小题,每小题3分,共30分)
-
1. 实数 的值是( )A、3 B、-3 C、±3 D、±92. 若代数式 在实数范围内有意义,则实数x的取值范围是( )A、x≠-3 B、x=-3 C、x<-3 D、x>-33. 计算(-a3)²的值为( )A、a5 B、a6 C、-a6 D、-a54. 下列说法中不正确的是( )A、抛掷一枚硬币,硬币落地时正面朝上是随机事件 B、把4个球放入三个抽屉中,其中一个抽屉中至少有2个球是必然事件 C、任意打开九年级下册数学教科书,正好是97页是确定事件 D、一只盒子中有白球3个,红球6个(每个球除了颜色外都相同),如果从中任取一个球,取得的是红球的概率大于白球的概率5. 下列式子正确的是( )A、(a-b)²=a²-2ab+b2 B、(a-b)²=a²-b² c.(a-b)²=a²+2ab+b² D.(a-b)²=a²-ab+b²6. 如图,将△ABC绕点C(0,1)旋转180°得到△DEC,若点A的坐标为(3,-1),则点D的坐标为( )
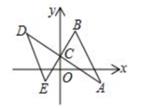 A、(-3,1) B、(-2,2) C、(-3,3) D、(-3,2)7. 如图是由若干个正方体组成的几何体的俯视图,数字表示该位置上小正方体的个数,则该几何体左视图可能是( )
A、(-3,1) B、(-2,2) C、(-3,3) D、(-3,2)7. 如图是由若干个正方体组成的几何体的俯视图,数字表示该位置上小正方体的个数,则该几何体左视图可能是( )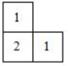 A、
A、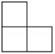 B、
B、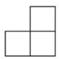 C、
C、 D、
D、 8. 某中学随机调查了15名学生,了解他们一周在校参加体育锻炼时间,列表如下:
8. 某中学随机调查了15名学生,了解他们一周在校参加体育锻炼时间,列表如下:锻炼时间(小时)
5
6
7
8
人数
2
6
5
2
则这15名同学一周在校参加体育锻炼时间的中位数和众数分别是( )
A、6,7 B、7,7 C、7,6 D、6,69. 小明训练上楼梯赛跑.他每步可上2阶或3阶(不上1阶),那么小明上12阶楼梯的不同方法共有( )(注:两种上楼梯的方法,只要有1步所踏楼梯阶数不相同,便认为是不同的上法。)A、15种 B、14种 C、13种 D、12种10. 当-2≤x≤1时,二次函数y=-(x-m)²+m²+1有最大值4,则实数m的值为( )A、 B、 或- C、2或- D、2或 或二、填空题(本大题共6个小题,每小题3分,共18分)
-
11. 计算7+(-2)的结果为。12. 计算 + = .13. 五张分别写有-1,2,0,-4,5的卡片(除数字不同以外,其余都相同),现从中任意取出一张卡片,则该卡片上的数字是负数的概率是。14. 如图,在平行四边形ABCD中,E为AB边上的点,BE=BC,将△ADE沿DE翻折,点A的对应点F恰好落在CE上,∠ADF=84°,则∠BEC=。
 15. 在平面直角坐标系中,A(4,0),直线l:y=6与y轴交于点B,点P是直线l上点B右侧的动点,以AP为边在AP右侧作等腰Rt△APQ,∠APQ=90°,当点P的横坐标满足0≤x≤8,则点Q的运动路径长为。16. 如图,在四边形ABCE中,∠ABC=45°,AE=CE,连接AC,∠ACB=30°,过A作AD⊥AE交BC于D,若AD=AE,则 =。
15. 在平面直角坐标系中,A(4,0),直线l:y=6与y轴交于点B,点P是直线l上点B右侧的动点,以AP为边在AP右侧作等腰Rt△APQ,∠APQ=90°,当点P的横坐标满足0≤x≤8,则点Q的运动路径长为。16. 如图,在四边形ABCE中,∠ABC=45°,AE=CE,连接AC,∠ACB=30°,过A作AD⊥AE交BC于D,若AD=AE,则 =。
三、解答题(共8题,共72分)
-
17. 解方程: x-1=2x+118. 如图,点B在线段AD上,BC∥DE,AB=ED,BC=DB。求证:∠A=∠E。
 19. 某校在推进新课改的过程中,开设的体育选修课有:A:篮球;B:足球;C:排球;D:羽毛球;E:乒乓球.学生可根据自己的爱好选修一门,体育老师对某班全体同学的选课情况进行调查统计,制成了两幅不完整的统计图。
19. 某校在推进新课改的过程中,开设的体育选修课有:A:篮球;B:足球;C:排球;D:羽毛球;E:乒乓球.学生可根据自己的爱好选修一门,体育老师对某班全体同学的选课情况进行调查统计,制成了两幅不完整的统计图。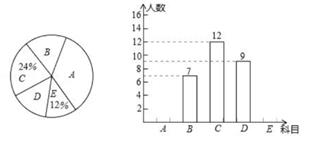 (1)、写出该班的总人数为 , 其中最喜爱篮球的有;在扇形统计图中,最喜爱足球的对应扇形的圆心角大小是 。(2)、若该校共有学生1500人,请估计其中选修篮球的大约有多少人?20. 某中学开学初到商场购买A.B两种品牌的足球,购买A种品牌的足球50个,B种品牌的足球25个,共花费4500元.已知购买一个B种品牌的足球比购买一个A种品牌的足球多花30元(1)、求购买一个A种品牌、一个B种品牌的足球各需多少元?(2)、学校为了响应习总书记“足球进校园”的号召,决定再次购进A.B两种品牌足球共50个,正好赶上商场对商品价格进行调整,A品牌足球售价比第一次购买时提高4元,B品牌足球按第一次购买时售价的9折出售,如果学校此次购买A.B两种品牌足球的总费用不超过第一次花费的70%,且保证这次购买的B种品牌足球不少于23个,则这次学校有哪几种购买方案?21. 如图,AC为⊙O的直径,DAB为⊙O的割线,E为⊙O上一点,弧BE=弧CE,DE⊥AB于D,交AO的延长线于F。
(1)、写出该班的总人数为 , 其中最喜爱篮球的有;在扇形统计图中,最喜爱足球的对应扇形的圆心角大小是 。(2)、若该校共有学生1500人,请估计其中选修篮球的大约有多少人?20. 某中学开学初到商场购买A.B两种品牌的足球,购买A种品牌的足球50个,B种品牌的足球25个,共花费4500元.已知购买一个B种品牌的足球比购买一个A种品牌的足球多花30元(1)、求购买一个A种品牌、一个B种品牌的足球各需多少元?(2)、学校为了响应习总书记“足球进校园”的号召,决定再次购进A.B两种品牌足球共50个,正好赶上商场对商品价格进行调整,A品牌足球售价比第一次购买时提高4元,B品牌足球按第一次购买时售价的9折出售,如果学校此次购买A.B两种品牌足球的总费用不超过第一次花费的70%,且保证这次购买的B种品牌足球不少于23个,则这次学校有哪几种购买方案?21. 如图,AC为⊙O的直径,DAB为⊙O的割线,E为⊙O上一点,弧BE=弧CE,DE⊥AB于D,交AO的延长线于F。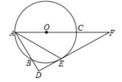 (1)、求证:DF为⊙O的切线;(2)、若AD= ,CF=3,求tan∠CAE的值。22. 如图1,直角三角形AOB中,∠AOB=90°,AB∥x轴,OA=2OB,AB=5,反比例函数y= (x>0)的图象经过点A。
(1)、求证:DF为⊙O的切线;(2)、若AD= ,CF=3,求tan∠CAE的值。22. 如图1,直角三角形AOB中,∠AOB=90°,AB∥x轴,OA=2OB,AB=5,反比例函数y= (x>0)的图象经过点A。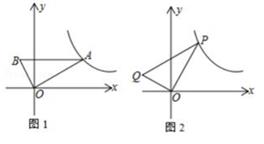 (1)、求反比例函数的解析式;(2)、如图2,将△AOB绕点O逆时针旋转得到△POQ。当Q坐标为(m,1)时,试判断点P是否在反比例函数y= (x>0)的图象上,并说明理由。23. 如图1,在Rt△ABC中,∠C=90°,AC=4,BC=3,点D,E分别在边BC,AC上。
(1)、求反比例函数的解析式;(2)、如图2,将△AOB绕点O逆时针旋转得到△POQ。当Q坐标为(m,1)时,试判断点P是否在反比例函数y= (x>0)的图象上,并说明理由。23. 如图1,在Rt△ABC中,∠C=90°,AC=4,BC=3,点D,E分别在边BC,AC上。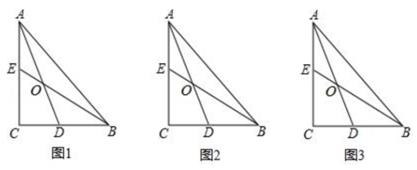 (1)、当BD=AE=2时,直接写出 = , =;(2)、如图2,若O为AD的中点,求证:(3)、如图3,当 ,∠AOE=∠BAC时,求AE的值。24. 二次函数y=x²-2mx-3m²(其中m是常数,且m>0)的图象与x轴分别交于点A、B(点A在点B左侧),在y轴交于C,点D在第四象限的抛物线上,连接AD,过点A作射线AE交抛物线于另一点E,AB平分∠DAE。(1)、若△ABC的面积为6,求抛物线的解析式;(2)、若点D、E的横坐标分别为a、b,求 的值;(3)、当DC∥x轴时,求 的值。
(1)、当BD=AE=2时,直接写出 = , =;(2)、如图2,若O为AD的中点,求证:(3)、如图3,当 ,∠AOE=∠BAC时,求AE的值。24. 二次函数y=x²-2mx-3m²(其中m是常数,且m>0)的图象与x轴分别交于点A、B(点A在点B左侧),在y轴交于C,点D在第四象限的抛物线上,连接AD,过点A作射线AE交抛物线于另一点E,AB平分∠DAE。(1)、若△ABC的面积为6,求抛物线的解析式;(2)、若点D、E的横坐标分别为a、b,求 的值;(3)、当DC∥x轴时,求 的值。