2015年福建省福州市中考数学真题试卷
试卷更新日期:2016-04-21 类型:中考真卷
一、选择题(共10小题,每小题3分,满分30分)
-
1. a的相反数是( )A、|a| B、 C、﹣a D、2. 下列图形中,由∠1=∠2能得到AB∥CD的是( )A、
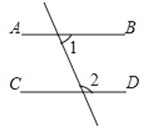 B、
B、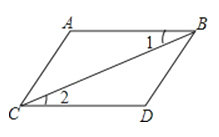 C、
C、 D、
D、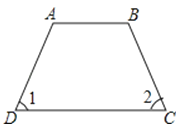 3. 不等式组的解集在数轴上表示正确的是( )A、
3. 不等式组的解集在数轴上表示正确的是( )A、 B、
B、 C、
C、 D、
D、 4. 计算3.8×107﹣3.7×107 , 结果用科学记数法表示为( )A、0.1×107 B、0.1×106 C、1×107 D、1×1065. 下列选项中,显示部分在总体中所占百分比的统计图是( )A、扇形图 B、条形图 C、折线图 D、直方图6. 计算a•a﹣1的结果为( )A、﹣1 B、0 C、1 D、-a7.
4. 计算3.8×107﹣3.7×107 , 结果用科学记数法表示为( )A、0.1×107 B、0.1×106 C、1×107 D、1×1065. 下列选项中,显示部分在总体中所占百分比的统计图是( )A、扇形图 B、条形图 C、折线图 D、直方图6. 计算a•a﹣1的结果为( )A、﹣1 B、0 C、1 D、-a7.如图,在3×3的正方形网格中由四个格点A,B,C,D,以其中一点为原点,网格线所在直线为坐标轴,建立平面直角坐标系,使其余三个点中存在两个点关于一条坐标轴对称,则原点是( )
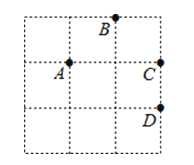 A、A点 B、B点 C、C点 D、D点8.
A、A点 B、B点 C、C点 D、D点8.如图,C,D分别是线段AB,AC的中点,分别以点C,D为圆心,BC长为半径画弧,两弧交于点M,测量∠AMB的度数,结果为( )
 A、80° B、90° C、100° D、105°9. 若一组数据1,2,3,4,x的平均数与中位数相同,则实数x的值不可能是( )A、0 B、2.5 C、3 D、510. 已知一个函数图象经过(1,﹣4),(2,﹣2)两点,在自变量x的某个取值范围内,都有函数值y随x的增大而减小,则符合上述条件的函数可能是( )A、正比例函数 B、一次函数 C、反比例函数 D、二次函数
A、80° B、90° C、100° D、105°9. 若一组数据1,2,3,4,x的平均数与中位数相同,则实数x的值不可能是( )A、0 B、2.5 C、3 D、510. 已知一个函数图象经过(1,﹣4),(2,﹣2)两点,在自变量x的某个取值范围内,都有函数值y随x的增大而减小,则符合上述条件的函数可能是( )A、正比例函数 B、一次函数 C、反比例函数 D、二次函数二、填空题(共6小题,满分24分)
-
11. 分解因式a2﹣9的结果是 .
12. 计算(x﹣1)(x+2)的结果是 .
13. 一个反比例函数图象过点A(﹣2,﹣3),则这个反比例函数的解析式是 .
14. 一组数据:2015,2015,2015,2015,2015,2015的方差是 .
15. 一个工件,外部是圆柱体,内部凹槽是正方体,如图所示,其中,正方体一个面的四个顶点都在圆柱底面的圆周上,若圆柱底面周长为2πcm,则正方体的体积为 cm3 .
16. 如图,在Rt△ABC中,∠ABC=90°,AB=BC= , 将△ABC绕点C逆时针旋转60°,得到△MNC,连接BM,则BM的长是 .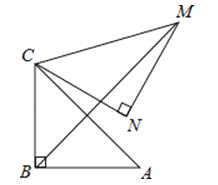
三、解答题
-
17. 计算:(-1)2015+sin30°+(2-)(2+).
18. 化简:19.如图,∠1=∠2,∠3=∠4,求证:AC=AD.
 20. 已知关于x的方程x2+(2m﹣1)x+4=0有两个相等的实数根,求m的值.21. 有48支队520名运动员参加篮球、排球比赛,其中每支篮球队10人,每支排球队12人,每名运动员只能参加一项比赛.问:篮球、排球队各有多少支?
20. 已知关于x的方程x2+(2m﹣1)x+4=0有两个相等的实数根,求m的值.21. 有48支队520名运动员参加篮球、排球比赛,其中每支篮球队10人,每支排球队12人,每名运动员只能参加一项比赛.问:篮球、排球队各有多少支?四、综合题
-
22. 一个不透明袋子中有1个红球,1个绿球和n个白球,这些球除颜色外无其他差别.(1)、当n=1时,从袋中随机摸出1个球,摸到红球和摸到白球的可能性是否相同?(在答题卡相应位置填“相同”或“不相同”);(2)、从袋中随机摸出一个球,记录其颜色,然后放回,大量重复该实验,发现摸到绿球的频率稳定于0.25,则n的值是(3)、在一个摸球游戏中,所有可能出现的结果如下:

根据树状图呈现的结果,求两次摸出的球颜色不同的概率.
23. 如图,Rt△ABC中,∠C=90°,AC= , tanB= , 半径为2的⊙C,分别交AC,BC于点D,E,得到 . (1)、求证:AB为⊙C的切线;(2)、求图中阴影部分的面积.24. 定义:长宽比为:1(n为正整数)的矩形称为矩形.
(1)、求证:AB为⊙C的切线;(2)、求图中阴影部分的面积.24. 定义:长宽比为:1(n为正整数)的矩形称为矩形.下面,我们通过折叠的方式折出一个矩形,如图①所示.


操作1:将正方形ABCD沿过点B的直线折叠,使折叠后的点C落在对角线BD上的点G处,折痕为BH.
操作2:将AD沿过点G的直线折叠,使点A,点D分别落在边AB,CD上,折痕为EF.
则四边形BCEF为矩形.
证明:设正方形ABCD的边长为1,则BD== .
由折叠性质可知BG=BC=1,∠AFE=∠BFE=90°,则四边形BCEF为矩形.
∴∠A=∠BFE.
∴EF∥AD.
∴= , 即= .
∴BF= .
∴BC:BF=1:=:1.
∴四边形BCEF为矩形.
阅读以上内容,回答下列问题:
(1)、在图①中,所有与CH相等的线段是 ,tan∠HBC的值是 ;
(2)、已知四边形BCEF为矩形,模仿上述操作,得到四边形BCMN,如图②,求证:四边形BCMN是矩形;(3)、将图②中的矩形BCMN沿用(2)中的方式操作3次后,得到一个“矩形”,则n的值是 .
25. 如图①,在锐角△ABC中,D,E分别为AB,BC中点,F为AC上一点,且∠AFE=∠A,DM∥EF交AC于点M. (1)、求证:DM=DA;(2)、点G在BE上,且∠BDG=∠C,如图②,求证:△DEG∽△ECF;(3)、在图②中,取CE上一点H,使∠CFH=∠B,若BG=1,求EH的长.
(1)、求证:DM=DA;(2)、点G在BE上,且∠BDG=∠C,如图②,求证:△DEG∽△ECF;(3)、在图②中,取CE上一点H,使∠CFH=∠B,若BG=1,求EH的长. 26. 如图,抛物线y=x2﹣4x与x轴交于O,A两点,P为抛物线上一点,过点P的直线y=x+m与对称轴交于点Q
26. 如图,抛物线y=x2﹣4x与x轴交于O,A两点,P为抛物线上一点,过点P的直线y=x+m与对称轴交于点Q (1)、这条抛物线的对称轴是 ,直线PQ与x轴所夹锐角的度数是 .
(1)、这条抛物线的对称轴是 ,直线PQ与x轴所夹锐角的度数是 .
(2)、若两个三角形面积满足S△POQ=S△PAQ , 求m的值(3)、当点P在x轴下方的抛物线上时,过点C(2,2)的直线AC与直线PQ交于点D,求:①PD+DQ的最大值;②PD•DQ的最大值.