人教A版（2019）数学必修第二册第八章立体几何初步

试卷更新日期：2020-04-21 类型：单元试卷

进入出卷网下载

一、单选题

1. 下列说法正确的是（）

A、三点确定一个平面 B、四边形一定是平面图形 C、梯形一定是平面图形 D、平面和平面有不同在一条直线上的三个交点

查看试题解析
2. 已知直线 $l ⊥$ 平面 $α$ ，直线 $m ∥$ 平面 $β$ ，若 $α ⊥ β$ ，则下列结论正确的是（）

A、 $l ∥ β$ 或 $l \subset β$ B、 $l / / m$ C、 $m ⊥ α$ D、 $l ⊥ m$

查看试题解析
3. 一个水平放置的平面图形的斜二测直观图是一个底角为 $45^{\circ}$ ，腰为 $\sqrt{2}$ ，上底长为 $2$ 的等腰梯形，那么原平面图形的面积为（）

A、 $3 \sqrt{2}$ B、 $6$ C、 $6 \sqrt{2}$ D、 $12 \sqrt{2}$

查看试题解析
4. 已知 $m$ ， $n$ 是空间内两条不同的直线， $α$ ， $β$ 是空间内两个不同的平面，下列说法正确的是（）

A、若 $m ⊥ n$ ， $m ⊥ α$ ，则 $n // α$ B、若 $α ⊥ β$ ， $α \cap β = m$ ， $n ⊥ m$ ，则 $n ⊥ α$ C、若 $α \cap β = m$ ， $n // α$ ，则 $m // n$ D、若 $m ⊥ α$ ， $n // β$ ， $α // β$ ，则 $m ⊥ n$

查看试题解析
5. 已知圆柱的轴截面为正方形，且圆柱的体积为 $54 π$ ，则该圆柱的侧面积为（）

A、 $27 π$ B、 $36 π$ C、 $54 π$ D、 $81 π$

查看试题解析
6. 已知四棱锥 $E - A B C D$ ，底面ABCD是边长为1的正方形， $E D = 1$ ，平面 $E C D ⊥$ 平面ABCD，当点C到平面ABE的距离最大时，该四棱锥的体积为（）

A、 $\frac{\sqrt{2}}{6}$ B、 $\frac{1}{3}$ C、 $\frac{\sqrt{2}}{3}$ D、1

查看试题解析
7. 如图，在长方体 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 中， $A B = 8$ ， $A D = 6$ ，异面直线 $B D$ 与 $A C_{1}$ 所成角的余弦值为 $\frac{1}{5}$ ，则该长方体外接球的表面积为（）

A、 $98 π$ B、 $196 π$ C、 $784 π$ D、 $\frac{1372}{3} π$

查看试题解析
8. 如图，在正四棱锥S－ABCD中，E，M，N分别是BC，CD，SC的中点，动点P在线段MN上运动时，下列四个结论：①EP⊥AC；②EP∥BD；③EP∥平面SBD；④EP⊥平面SAC，其中恒成立的为（）

A、①③ B、③④ C、①② D、②③④

查看试题解析
9. 唐朝著名的凤鸟花卉纹浮雕银杯如图1所示，它的盛酒部分可以近似地看作是半球与圆柱的组合体（如图2）.当这种酒杯内壁表面积（假设内壁表面光滑，表面积为 $S$ 平方厘米，半球的半径为 $R$ 厘米）固定时，若要使得酒杯的容积不大于半球体积的2倍，则 $R$ 的取值范围为（）

A、 $(0 ， \sqrt{\frac{35}{10 π}}]$ B、 $[\sqrt{\frac{3 S}{10 π}} ， + \infty)$ C、 $(\sqrt{\frac{S}{5 π}} ， \sqrt{\frac{3 S}{10 π}}]$ D、 $[\sqrt{\frac{3 S}{10 π}} ， \sqrt{\frac{S}{2 π}})$

查看试题解析
10. 已知 $A, B$ 是球 $O$ 的球面上的两点， $∠ A O B = 90^{\circ}, C$ 为球面上的动点.若三棱锥 $O - A B C$ 的体积最大值为 $36$ ，则球的表面积为（）

A、 $144 π$ B、 $256 π$ C、 $64 π$ D、 $36 π$

查看试题解析
11. 如图，矩形 $A B C D$ 中， $A B = 2 A D$ ， $E$ 为边 $A B$ 的中点，将 $Δ A D E$ 沿直线 $D E$ 翻折成 $Δ A_{1} D E$ ．若 $M$ 为线段 $A_{1} C$ 的中点，则在 $Δ A D E$ 翻折过程中，下面四个命题中不正确的是（）

A、 $| B M |$ 是定值 B、点 $M$ 在某个球面上运动 C、存在某个位置，使 $D E ⊥ A_{1} C$ D、存在某个位置，使 $M B //$ 平面 $A_{1} D E$

查看试题解析
12. 已知四面体ABCD中，棱BC，AD所在直线所成的角为60°，且BC=2，AD=3，∠ACD=120°，则四面体ABCD体积的最大值是（）

A、 $\frac{\sqrt{3}}{2}$ B、 $\frac{\sqrt{3}}{4}$ C、 $\frac{9}{4}$ D、 $\frac{3}{4}$

查看试题解析
13. 如图，棱长为2的正方体 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 中， $M$ 是棱 $A A_{1}$ 的中点，点 $P$ 在侧面 $A B B_{1} A_{1}$ 内，若 $D_{1} P ⊥ C M$ ，则 $Δ P B C$ 的面积的最小值为（）

A、 $\frac{2 \sqrt{5}}{5}$ B、 $\frac{\sqrt{5}}{5}$ C、 $\frac{4}{5}$ D、1

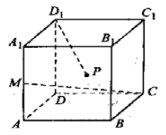查看试题解析
14. 已知正四棱柱 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 的底面边长为1，高为2，M为 $B_{1} C_{1}$ 的中点，过M作平面 $α$ ，使得平面 $α //$ 平面 $A_{1} B D$ ，若平面 $α$ 把 $A B C - A_{1} B_{1} C_{1}$ 分成的两个几何体中，体积较小的几何体的体积为（）

A、 $\frac{1}{48}$ B、 $\frac{1}{24}$ C、 $\frac{1}{12}$ D、 $\frac{1}{8}$

查看试题解析

二、填空题

15. 已知圆锥的母线长为 $10 c m$ ，侧面积为 $60 π c m^{2}$ ，则此圆锥的体积为 $c m^{3}$ .

查看试题解析
16. 若一个球的体积是其半径的 $\frac{4}{3}$ 倍，则该球的表面积为．

查看试题解析
17. 已知四边形 $A B C D$ 为矩形， $A B = 2 A D = 4$ ， $M$ 为 $A B$ 的中点，将 $Δ A D M$ 沿 $D M$ 折起，得到四棱锥 $A_{1} - D M B C$ ，设 $A_{1} C$ 的中点为 $N$ ，在翻折过程中，得到如下有三个命题：
① $B N / /$ 平面 $A_{1} D M$ ，且 $B N$ 的长度为定值 $\sqrt{5}$ ；

②三棱锥 $N - D M C$ 的最大体积为 $\frac{2 \sqrt{2}}{3}$ ；

③在翻折过程中，存在某个位置，使得 $D M ⊥ A_{1} C$ .

其中正确命题的序号为．（写出所有正确结论的序号）

查看试题解析
18. 中国古代数学经典《九章算术》系统地总结了战国、秦、汉时期的数学成就，书中将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马，将四个面都为直角三角形的三棱锥称之为鳖臑，如图为一个阳马与一个鳖臑的组合体，已知 $P A ⊥$ 平面 $A B C E$ ，四边形 $A B C D$ 为正方形， $A D = 2$ ， $E D = 1$ ，若鳖臑 $P - A D E$ 的外接球的体积为 $\frac{9}{2} π$ ，则阳马 $P - A B C D$ 的外接球的表面积等于．

查看试题解析

三、解答题

19. 如图所示，在边长为a正方体 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 中， $E ， F ， G ， H$ 分别为棱 $C C_{1} ， B C ， A B ， D_{1} C_{1}$ 的中点.

(1)、求证：点 $E ， F ， G ， H$ 四点共面；

(2)、求三棱锥 $B - A_{1} C_{1} D$ 的体积。

查看试题解析
20. 在四棱锥P﹣ABCD中，底面ABCD为平行四边形，PD⊥平面ABCD，BD＝CD，E，F分别为BC，PD的中点．

(1)、求证：EF∥平面PAB；

(2)、求证：平面PBC⊥平面EFD．

查看试题解析
21. 如图，已知 $B D$ 为圆锥 $A O$ 底面的直径，点 $C$ 是圆锥底面的圆周上， $A B = B D = 2$ ， $∠ B D C = \frac{π}{6}$ ， $A E = E D$ ， $F$ 是 $A C$ 上一点，且平面 $B F E ⊥$ 平面 $A B D$ .

（Ⅰ）求证 $A D ⊥ B F$ ；

（Ⅱ）求多面体 $B C D E F$ 的体积.

查看试题解析
22. 如图，在矩形 $A B C D$ 中， $A B = 4$ ， $A D = 2$ ， $E$ 是 $C D$ 的中点，以 $A E$ 为折痕将 $Δ D A E$ 向上折起， $D$ 变为 $D'$ ，且平面 $D' A E ⊥$ 平面 $A B C E$ .

(1)、求三棱锥 $A - D' C E$ 的体积；

(2)、求证： $A D' ⊥ B E$ ；

(3)、求证：平面 $A B D' ⊥$ 平面 $B D^{'} E$

查看试题解析
23. 如图，在四棱锥 $P - A B C D$ 中， $A B ∥ C D$ ，且 $∠ B A P = ∠ C D P = 90 °$ .

(1)、证明：平面 $P A B ⊥$ 平面 $P A D$ ；

(2)、若 $P A = P D = A B = D C$ ， $∠ A P D = 90 °$ ，且四棱锥 $P - A B C D$ 的体积为 $\frac{8}{3}$ ，求该四棱锥的侧面积．

查看试题解析
24. 设三棱锥 $P - A B C$ 的每个顶点都在球 $O$ 的球面上， $Δ P A B$ 是面积为 $3 \sqrt{3}$ 的等边三角形， $A C ⊥ B C$ ， $A C = B C$ ，且平面 $P A B ⊥$ 平面 $A B C$ .

(1)、求球 $O$ 的表面积；

(2)、证明：平面 $P O C ⊥$ 平面 $A B C$ ，且平面 $P O C ⊥$ 平面 $P A B$ .

(3)、与侧面 $P A B$ 平行的平面 $α$ 与棱 $A C$ ， $B C$ ， $P C$ 分别交于 $D$ ， $E$ ， $F$ ，求四面体 $O D E F$ 的体积的最大值.

查看试题解析

人教A版（2019）数学必修第二册 第八章 立体几何初步

一、单选题

二、填空题

三、解答题

人教A版（2019）数学必修第二册第八章立体几何初步