人教A版(2019)数学必修第二册 8.6 空间直线、平面的垂直
试卷更新日期:2020-04-21 类型:同步测试
一、单选题
-
1. 已知三棱锥A-BCD中,AD⊥BC,AD⊥CD,则有( )A、平面ABC⊥平面ADC B、平面ADC⊥平面BCD C、平面ABC⊥平面BDC D、平面ABC⊥平面ADB2. 如图,在三棱锥 中,侧面 底面BCD, , , , ,直线AC与底面BCD所成角的大小为
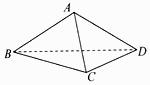 A、 B、 C、 D、3. 已知三棱锥 中,若PA,PB,PC两两互相垂直,作 面ABC,垂足为O,则点O是 的( )A、外心 B、内心 C、重心 D、垂心4. 下列命题中错误的是( )A、如果平面α⊥平面β,那么平面α内一定存在直线平行于平面β B、如果平面α不垂直于平面β,那么平面α内一定不存在直线垂直于平面β C、如果平面α⊥平面γ,平面β⊥平面γ,α∩β=l,那么l⊥平面γ D、如果平面α⊥平面β,那么平面α内所有直线都垂直于平面β5. 如图,PA⊥☉O所在的平面,AB是☉O的直径,C是☉O上的一点,AE⊥PB于E,AF⊥PC于F,给出下列结论:①BC⊥平面PAC;②AF⊥平面PCB;③EF⊥PB;④AE⊥平面PBC.其中正确命题的个数是( )
A、 B、 C、 D、3. 已知三棱锥 中,若PA,PB,PC两两互相垂直,作 面ABC,垂足为O,则点O是 的( )A、外心 B、内心 C、重心 D、垂心4. 下列命题中错误的是( )A、如果平面α⊥平面β,那么平面α内一定存在直线平行于平面β B、如果平面α不垂直于平面β,那么平面α内一定不存在直线垂直于平面β C、如果平面α⊥平面γ,平面β⊥平面γ,α∩β=l,那么l⊥平面γ D、如果平面α⊥平面β,那么平面α内所有直线都垂直于平面β5. 如图,PA⊥☉O所在的平面,AB是☉O的直径,C是☉O上的一点,AE⊥PB于E,AF⊥PC于F,给出下列结论:①BC⊥平面PAC;②AF⊥平面PCB;③EF⊥PB;④AE⊥平面PBC.其中正确命题的个数是( ) A、1 B、2 C、3 D、46. 如图,在长方体 中, , ,则下列结论中正确的是( )
A、1 B、2 C、3 D、46. 如图,在长方体 中, , ,则下列结论中正确的是( ) A、 ∥ B、 ∥平面 C、 D、 平面7. 如图所示,平面四边形 中, , ,将其沿对角线 折成四面体 ,使平面 平面 ,则下列说法中不正确的是( )
A、 ∥ B、 ∥平面 C、 D、 平面7. 如图所示,平面四边形 中, , ,将其沿对角线 折成四面体 ,使平面 平面 ,则下列说法中不正确的是( ) A、 B、 C、 D、8. 如图,点E为正方形ABCD边CD上异于点C,D的动点,将△ADE沿AE翻折成△SAE,使得平面SAE⊥平面ABCE,则下列说法中正确的有( )
A、 B、 C、 D、8. 如图,点E为正方形ABCD边CD上异于点C,D的动点,将△ADE沿AE翻折成△SAE,使得平面SAE⊥平面ABCE,则下列说法中正确的有( )①存在点E使得直线SA⊥平面SBC;
②平面SBC内存在直线与SA平行
③平面ABCE内存在直线与平面SAE平行;
④存在点E使得SE⊥BA.
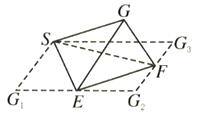
 A、1个 B、2个 C、3个 D、4个9. 在三棱锥P-ABC中,平面PAC⊥平面ABC,∠PCA=90°,△ABC是边长为4的正三角形,PC=4,M是AB边上的一动点,则PM的最小值为( )A、2 B、 C、4 D、410. 如图所示,在正方形 中, 分别是 的中点,现在沿 把这个正方形折成一个四面体,使 三点重合,重合后的点记为 .给出下列关系:
A、1个 B、2个 C、3个 D、4个9. 在三棱锥P-ABC中,平面PAC⊥平面ABC,∠PCA=90°,△ABC是边长为4的正三角形,PC=4,M是AB边上的一动点,则PM的最小值为( )A、2 B、 C、4 D、410. 如图所示,在正方形 中, 分别是 的中点,现在沿 把这个正方形折成一个四面体,使 三点重合,重合后的点记为 .给出下列关系:① 平面 ;② 平面 ;③ ;④ 上平面 .其中关系成立的有( )
 A、①② B、①③ C、②③ D、③④11. 在空间四边形ABCD中,平面ABD⊥平面BCD,且DA⊥平面ABC,则△ABC的形状是( )A、锐角三角形 B、直角三角形 C、钝角三角形 D、不能确定12. 如图,已知 是顶角为 的等腰三角形,且 ,点 是 的中点.将 沿 折起,使得 ,则此时直线 与平面 所成角的正弦值为( )
A、①② B、①③ C、②③ D、③④11. 在空间四边形ABCD中,平面ABD⊥平面BCD,且DA⊥平面ABC,则△ABC的形状是( )A、锐角三角形 B、直角三角形 C、钝角三角形 D、不能确定12. 如图,已知 是顶角为 的等腰三角形,且 ,点 是 的中点.将 沿 折起,使得 ,则此时直线 与平面 所成角的正弦值为( )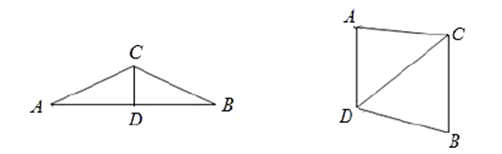 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
13. 如图,直线AB⊥平面BCD , ∠BCD=90°,则图中直角三角形的个数为 .
 14. 在直三棱柱 中, .有下列条件:
14. 在直三棱柱 中, .有下列条件:① ;② ;③ .其中能成为 的充要条件的是 . (填上序号)
 15.
15.如图,矩形ABCD中,AB=1,BC=a,PA⊥平面ABCD,若在BC上只有一个点Q满足PQ⊥DQ,则a的值等于
 16. 设M、N是直角梯形ABCD两腰的中点,DE⊥AB于E(如图),AE=EB=DE=2.现将△ADE沿DE折起,使二面角A﹣DE﹣B为90°,P,Q分别是线段AE和线段EB上任意一点,若MQ⊥PN时,求PQ长度的取值范围
16. 设M、N是直角梯形ABCD两腰的中点,DE⊥AB于E(如图),AE=EB=DE=2.现将△ADE沿DE折起,使二面角A﹣DE﹣B为90°,P,Q分别是线段AE和线段EB上任意一点,若MQ⊥PN时,求PQ长度的取值范围
三、解答题
-
17. 如图,已知直角梯形ABCD中,AB∥CD,AB⊥BC,AB=1,BC=2,CD=1+ ,过A作AE⊥CD,垂足为E,现将△ADE沿AE折叠,使得DE⊥EC.
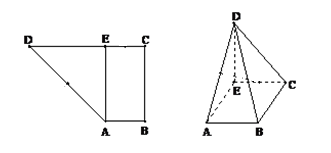 (1)、求证:BC⊥面CDE;(2)、在线段AE上是否存在一点R,使得面BDR⊥面DCB,若存在,求出点R的位置;若不存在,请说明理由.18. 如图,在矩形 中, , , 是 的中点,以 为折痕将 向上折起, 变为 ,且平面 平面 .
(1)、求证:BC⊥面CDE;(2)、在线段AE上是否存在一点R,使得面BDR⊥面DCB,若存在,求出点R的位置;若不存在,请说明理由.18. 如图,在矩形 中, , , 是 的中点,以 为折痕将 向上折起, 变为 ,且平面 平面 . (1)、求证: ;(2)、求二面角 的大小.19. 如图,矩形 中, , ,点 是 上的动点.现将矩形 沿着对角线 折成二面角 ,使得 .
(1)、求证: ;(2)、求二面角 的大小.19. 如图,矩形 中, , ,点 是 上的动点.现将矩形 沿着对角线 折成二面角 ,使得 .
(Ⅰ)求证:当 时, ;
(Ⅱ)试求 的长,使得二面角 的大小为 .


