人教A版（2019）数学必修第二册 8.5 空间直线、平面的平行

试卷更新日期：2020-04-21 类型：同步测试

进入出卷网下载

一、单选题

1. 平行于同一平面的两条直线的位置关系（）

A、平行 B、相交 C、异面 D、平行、相交或异面

查看试题解析
2. 若两个平面互相平行，则分别在这两个平行平面内的直线（）

A、平行 B、异面 C、相交 D、平行或异面

查看试题解析
3. 如图，正方体 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 中， $E$ ， $F$ ， $G$ ， $H$ 分别为所在棱的中点，则下列各直线中，不与平面 $A C D_{1}$ 平行的是（）

A、直线 $E F$ B、直线 $G H$ C、直线 $E H$ D、直线 $A_{1} B$

查看试题解析
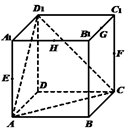4. 如图，四棱锥P-ABCD中，M，N分别为AC，PC上的点，且MN∥平面PAD，则（）

A、MN∥PD B、MN∥PA C、MN∥AD D、以上均有可能

查看试题解析
5. 如图，下列四个正方体图形中，A、B为正方体的两个顶点，M、N、P分别为其所在棱的中点，能得出AB∥平面MNP的图形序号是（）

A、①③ B、①④ C、②③ D、②④

查看试题解析
6. 下列说法中正确的个数是（）
①平面α与平面β ， γ都相交，则这三个平面有2条或3条交线；②如果a ， b是两条直线，a∥b ，那么a平行于经过b的任何一个平面；③直线a不平行于平面α ，则a不平行于α内任何一条直线；④如果α∥β ， a∥α ，那么a∥β.

A、0个 B、1个 C、2个 D、3个

查看试题解析
7. 如图，在直二面角A﹣BD﹣C中，△ABD、△CBD均是以BD为斜边的等腰直角三角形，取AD中点E，将△ABE沿BE翻折到△A₁BE，在△ABE的翻折过程中，下列不可能成立的是（）

A、BC与平面A₁BE内某直线平行 B、CD∥平面A₁BE C、BC与平面A₁BE内某直线垂直 D、BC⊥A₁B

查看试题解析
8. $a 、 b 、 c$ 为三条不重合的直线，α、β、γ为三个不重合平面，现给出六个命题：
① $\begin{matrix} a ∥ c \\ b ∥ c \end{matrix}} \Rightarrow a ∥ b$ ；② $\begin{matrix} a ∥ γ \\ b ∥ γ \end{matrix}} \Rightarrow a ∥ b$ ；③ $\begin{matrix} a ∥ c \\ β ∥ c \end{matrix}} \Rightarrow a ∥ β$ ；
④ $\begin{matrix} a ∥ γ \\ β ∥ γ \end{matrix}} \Rightarrow a ∥ β$ ；⑤ $\begin{matrix} α ∥ c \\ a ∥ c \end{matrix}} \Rightarrow α ∥ a$ ；⑥ $\begin{matrix} α ∥ γ \\ a ∥ γ \end{matrix}} \Rightarrow α ∥ a$
其中正确的命题是（）

A、①②③ B、①④⑤ C、①④ D、①③④

查看试题解析
9. 正方体 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 的棱长为3，点E在A₁B₁上，且B₁E=1，平面α∥平面BC₁E（平面α是图中阴影平面），若平面α∩平面AA₁B₁B=A₁F，则AF的长为（）

A、1 B、1.5 C、2 D、3

查看试题解析
10. 如图，在四面体ABCD中，若截面PQMN是正方形，则在下列结论中错误的为（）

A、AC⊥BD B、AC∥截面PQMN C、AC＝BD D、异面直线PM与BD所成的角为45°

查看试题解析
11. 如图，在棱长为1的正方体 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 中，点 $E$ ， $F$ 分别是棱 $B C$ ， $C C_{1}$ 的中点， $P$ 是侧面 $B C C_{1} B_{1}$ 内一点，若 $A_{1} P ∥ 平面 A E F$ ，则线段 $A_{1} P$ 长度的取值范围是（）

A、 $(\frac{3 \sqrt{2}}{4} ， \frac{\sqrt{5}}{2})$ B、 $[\frac{3 \sqrt{2}}{4} ， \frac{\sqrt{5}}{2}]$ C、 $[1 ， \frac{\sqrt{5}}{2}]$ D、 $[0 ， \frac{\sqrt{5}}{2}]$

查看试题解析
12. 在正四棱柱 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 中，顶点 $B_{1}$ 到对角线 $B D_{1}$ 和到平面 $A_{1} B C D_{1}$ 的距离分别为 $h$ 和 $d$ ，则下列命题中正确的是（）

A、若侧棱的长小于底面的变长，则 $\frac{h}{d}$ 的取值范围为 $(0 ， 1)$ B、若侧棱的长小于底面的变长，则 $\frac{h}{d}$ 的取值范围为 $(\frac{\sqrt{2}}{2} ， \frac{2 \sqrt{3}}{3})$ C、若侧棱的长大于底面的变长，则 $\frac{h}{d}$ 的取值范围为 $(\frac{2 \sqrt{3}}{3} ， \sqrt{2})$ D、若侧棱的长大于底面的变长，则 $\frac{h}{d}$ 的取值范围为 $(\frac{2 \sqrt{3}}{3} ， + \infty)$

查看试题解析

二、填空题

13. 在正方体 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 的12条棱中，与平面 $B C_{1} D_{1}$ 平行的棱共有条.

查看试题解析
14. 如图是正方体的平面展开图．在这个正方体中，
①BM∥平面DE；②CN∥平面AF；③平面BDM∥平面AFN；④平面BDE∥平面NCF.

以上四个命题中，正确命题的序号是．

查看试题解析
15. 如图，在正方体ABCD－A₁B₁C₁D₁中，M，N，P分别是C₁C， C₁B₁ ， C₁D₁的中点，点H在四边形A₁ADD₁的边及其内部运动，则H满足条件时，有BH∥平面MNP.

查看试题解析
16. 如图所示， $A B C D - A_{1} B_{1} C_{1} D_{1}$ 是棱长为a的正方体，M、N分别是棱A₁B₁、B₁C₁的中点，P是棱AD上的一点，AP＝ $\frac{a}{3}$ ，过P，M，N的平面交上底面于PQ，Q在CD上，则PQ＝．

查看试题解析

三、解答题

17. 如图，在四棱锥 $P - A B C D$ 中， $A B / / D C$ ， $C D = 2 A B$ ， $E$ 为棱 $P D$ 的中点.

(1)、求证： $A E$ $//$ 平面 $P B C$ ；

(2)、试判断 $P B$ 与平面 $A E C$ 是否平行？并说明理由.

查看试题解析
18. 如图所示，四棱锥 $P - A B C D$ 中， $P A ⊥ A B ， P A ⊥ A D$ ( $P A$ 是四棱锥 $P - A B C D$ 的高)， $A D / / B C ，$ $A B = A D$ $= A C = 3 ，$ $P A = B C$ $= 4 ， P B = 5 ， M$ 为线段 $A D$ 上一点， $A M = 2 M D$ ， $N$ 为 $P C$ 的中点.

(1)、证明： $M N ∥$ 平面 $P A B$ ；

(2)、求三棱锥 $C - B M N$ 的体积.

查看试题解析
19. 如图， $A B C D$ 是边长为3的正方形， $D E ⊥$ 平面 $A B C D$ ， $A F ⊥$ 平面 $A B C D$ ， $D E = 3 A F = 3$ .

(1)、证明：平面 $A B F / /$ 平面 $D C E$ ；

(2)、在 $D E$ 上是否存在一点 $G$ ，使平面 $F B G$ 将几何体 $A B C D E F$ 分成上下两部分的体积比为 $3 ： 11$ ？若存在，求出点 $G$ 的位置；若不存在，请说明理由.

查看试题解析
20. 在正方体ABCD－A₁B₁C₁D₁中，如图．

(1)、求证：平面AB₁D₁∥平面C₁BD；

(2)、试找出体对角线A₁C与平面AB₁D₁和平面C₁BD的交点E，F，并证明：A₁E＝EF＝FC.

查看试题解析