内蒙古满洲里市2020年中考数学一模考试试卷

试卷更新日期：2020-04-21 类型：中考模拟

进入出卷网下载

一、选择题（下列各题的四个选项中只有一个符合题意.共12小题，每小题3分，共36分）

1. 4的算术平方根是（）

A、2 B、﹣2 C、±2 D、 $\sqrt{2}$

查看试题解析
2. 下列图形中既是轴对称图形又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 下列计算正确是（）

A、3x﹣x＝3 B、a³÷a⁴＝ $\frac{1}{a}$ C、（x﹣1）²＝x²﹣2x+1 D、（﹣2a²）³＝﹣6a⁶

查看试题解析
4. 如图，是由几个大小相同的小立方块所搭几何体的俯视图，其中小正方形中的数字表示在该位置的小立方块的个数，则这个几何体的主视图是（）

A、 B、 C、 D、

查看试题解析
5. 下列对一元二次方程x²+x﹣3＝0根的情况的判断，正确是（）

A、有两个不相等实数根 B、有两个相等实数根 C、有且只有一个实数根 D、没有实数根

查看试题解析
6. 一组数据1，3，4，4，4，5，5，6的众数和方差分别是（）

A、4，1 B、4，2 C、5，1 D、5，2

查看试题解析
7. 如图，某社会实践活动小组实地测量两岸互相平行的一段河的宽度，在河的南岸点A处，测得河的北岸边点B在其北偏东45°方向，然后向西走60米到达C点，测得点B在点C的北偏东60°方向，则这段河的宽度为（）

A、60( $\sqrt{3}$ +1)米 B、30( $\sqrt{3}$ +1)米 C、(90﹣30 $\sqrt{3}$ )米 D、30( $\sqrt{3}$ ﹣1)米

查看试题解析
8. 某工厂新引进一批电子产品，甲工人比乙工人每小时多搬运30件电子产品，已知甲工人搬运300件电子产品所用的时间与乙工人搬运200件电子产品所用的时间相同 $.$ 若设乙工人每小时搬运x件电子产品，可列方程为 $($ 　　 $)$

A、 $\frac{300}{x} = \frac{200}{x + 30}$ B、 $\frac{300}{x - 30} = \frac{200}{x}$ C、 $\frac{300}{x + 30} = \frac{200}{x}$ D、 $\frac{300}{x} = \frac{200}{x - 30}$

查看试题解析
9. 如图，在△ABC中，AB＝AC ， ∠BAC＝100°，在同一平面内，将△ABC绕点A顺时针旋转到△AB₁C₁的位置，连接BB₁ ，若BB₁∥AC₁ ，则∠CAC₁的度数是（）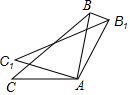

A、10° B、20° C、30° D、40°

查看试题解析
10. 某学习小组做“用频率估计概率”的试验时，统计了某一结果出现的频率，绘制了如下折线统计图，则符合这一结果的试验最有可能的是（）

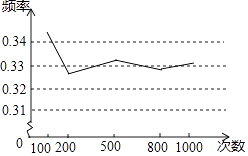A、袋中装有大小和质地都相同的3个红球和2个黄球，从中随机取一个，取到红球 B、掷一枚质地均匀的正六面体骰子，向上的面的点数是偶数 C、先后两次掷一枚质地均匀的硬币，两次都出现反面 D、先后两次掷一枚质地均匀的正六面体骰子，两次向上的面的点数之和是7或超过9

查看试题解析
11. 如图，在平面直角坐标系中，等腰直角三角形ABC的顶点A、B分别在x轴、y轴的正半轴上，∠ABC＝90°，CA⊥x轴，点C在函数y＝ $\frac{k}{x}$ （x＞0）的图象上，若AB＝2，则k的值为（）

A、4 B、2 $\sqrt{2}$ C、2 D、 $\sqrt{2}$

查看试题解析
12. 如图，点A在线段BD上，在BD的同侧作等腰Rt△ABC和等腰Rt△ADE ，其中∠ABC＝∠AED＝90°，CD与BE、AE分别交于点P、M ．对于下列结论：
①△CAM∽△DEM；②CD＝2BE；③MP•MD＝MA•ME；④2CB²＝CP•CM ．

其中正确是（）

A、①② B、①②③ C、①③④ D、①②③④

查看试题解析

二、填空题

13. 因式分解：x³﹣25x ．

查看试题解析
14. 半径为10cm的半圆围成一个圆锥，则这个圆锥的高是cm．

查看试题解析
15. 当 $x = 2$ 时，代数式 $(\frac{2 x + 1}{x} + x) \div \frac{x + 1}{x}$ 的值是．

查看试题解析
16. 直角三角形的外接圆半径为5，内切圆半径为2，则此三角形周长为．

查看试题解析
17. 我国古代数学家杨辉发现了如图所示的三角形，我们称之为“杨辉三角”从图中取一列数：1，3，6，10，…，记a₁＝1，a₂＝3，a₃＝6，a₄＝10，…，那么a₄+a₁₁﹣2a₁₀+10的值是．

查看试题解析

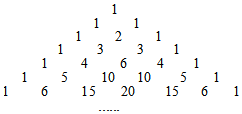
三、解答题（本题4个小题，每小题6分，共24分）

18. 计算：（﹣1）²⁰¹⁸﹣ $\sqrt{8}$ +（π﹣3）⁰+4cos45°．

查看试题解析
19. 解不等式组： ${\begin{array}{l} 2 x + 1 > x \\ \frac{x + 5}{2} - x \geq 1 \end{array}$ ，并把解集在数轴上表示出来.

查看试题解析
20. 已知直线y＝kx+b与直线y＝2x+1平行，且过点（1，﹣3）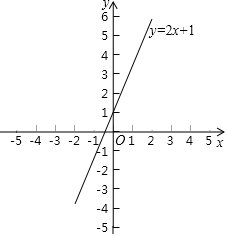

(1)、求这个一次函数的关系式？

(2)、画出函数图象．

(3)、该函数图象与两个坐标轴围成的三角形的面积？

查看试题解析
21. 完全相同的四张卡片，上面分别标有数字1，2，﹣1，﹣2，将其背面朝上，从中任意抽出两张（不放回），把第一张的数字记为a，第二张的数字记为b，以a、b分别作为一个点的横坐标与纵坐标；求点（a，b）在第四象限的概率．（用树状图或列表法求解）

查看试题解析

四、（本题7分）

22. 如图，在四边形ABCD中，对角线AC ， BD相交于点O ， AO＝CO ， BO＝DO ，且∠ABC+∠ADC＝180°．

(1)、求证：四边形ABCD是矩形；

(2)、若∠ADF：∠FDC＝3：2，DF⊥AC ，求∠BDF的度数．

查看试题解析

五、（本题7分）

23. 今年是我市全面推进中小学校“社会主义核心价值观”教育年．某校对全校学生进行了中期检测评价，检测结果分为A（优秀）、B（良好）、C（合格）、D（不合格）四个等级．并随机抽取若干名学生的检测结果作为样本进行数据处理，制作了如下所示不完整的统计表和统计图．

等级

频数

频率

A

a

0.3

B

35

0.35

C

31

b

D

4

0.04

请根据图提供的信息，解答下列问题：

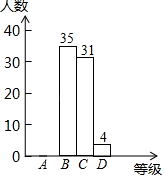(1)、本次随机抽取的样本容量为；

(2)、a＝， b＝；

(3)、请在图2中补全条形统计图；

(4)、若该校共有学生800人，据此估算，该校学生在本次检测中达到“A（优秀）”等级的学生人数为人．

查看试题解析

六、（本题8分）

24. 如图，在△ABC中，AB＝AC ，以AB为直径的⊙O分别交AC ， BC于点D ， E ，过点B作⊙O的切线，交AC的延长线于点F ．

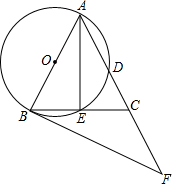(1)、求证：∠CBF＝ $\frac{1}{2}$ ∠CAB；

(2)、若CD＝2，tan∠CBF＝ $\frac{1}{2}$ ，求FC的长．

查看试题解析

七、（本题10分）

25. 小明大学毕业回家乡创业，第一期培植盆景与花卉各40盆售后统计，盆景的平均每盆利润是160元，花卉的平均每盆利润是19元，调研发现：
①盆景每增加1盆，盆景的平均每盆利润减少2元；每减少1盆，盆景的平均每盆利润增加2元；②花卉的平均每盆利润始终不变．

小明计划第二期培植盆景与花卉共80盆，设培植的盆景比第一期增加x盆，第二期盆景与花卉售完后的利润分别为W₁ ， W₂（单位：元）

(1)、用含x的代数式分别表示W₁ ， W₂；

(2)、当x取何值时，第二期培植的盆景与花卉售完后获得的总利润W最大，最大总利润是多少？

查看试题解析

八、（本题13分）

26. 如图，在Rt△ABC中，∠C＝90°，∠A＝30°，AB＝4，动点P从点A出发，沿AB以每秒2个单位长度的速度向终点B运动．过点P作PD⊥AC于点D（点P不与点A、B重合），作∠DPQ＝60°，边PQ交射线DC于点Q ．设点P的运动时间为t秒．

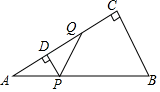(1)、用含t的代数式表示线段DC的长；

(2)、当点Q与点C重合时，求t的值；

(3)、设△PDQ与△ABC重叠部分图形的面积为S ，求S与t之间的函数关系式；

(4)、当线段PQ的垂直平分线经过△ABC一边中点时，直接写出t的值．

查看试题解析

等级	频数	频率
A	a	0.3
B	35	0.35
C	31	b
D	4	0.04