山西省2020年中考数学线上大模考二模考试试卷
试卷更新日期：2020-04-21 类型：中考模拟
一、选择题
-
1. 计算4﹣（﹣1）的结果等于（ ）A、4 B、﹣4 C、3 D、52. 已知直线l1∥l2 ， 将一块含30°角的直角三角板ABC按如图所示方式放置，若∠1＝85°，则∠2等于（ ）
A、35° B、45° C、55° D、65°3. 不等式组 的解集是（ ）A、1＜x≤3 B、x＞1 C、x≤3 D、x≥34. 下列运算不正确是（ ）A、（a2）3÷a4＝a2 B、（﹣ a2）•（﹣2a）＝﹣5a3 C、（2﹣ ）0＝1 D、a3+a3＝2a35. 2019年12月25日是中国伟大领神毛泽东同志诞辰126周年纪念日，某校举行以“高楼万丈平地起，幸福不忘毛主席”为主题的演讲比赛，最终有15名同学进入決赛（他们決赛的成绩各不相同）、比赛将评出一等奖1名，二等奖2名，三等奖4名．某参赛选手知道自己的分数后，要判断自己能否获奖，他需要知道这15名学生成绩的（ ）A、平均数 B、方差 C、众数 D、中位数6. 口罩成为需求最为迫切的防护物资．在这个关键时刻，我国某企业利用自身优势转产口罩，这背后不仅体现出企业强烈的社会责任感，更是我国人民团结﹣﹣心抗击疫情的决心据悉该企业3月份的口罩日产能已达到500万只，预计今后数月内都将保持同样的产能，则3月份（按31天计算）该企业生产的口罩总数量用科学记数法表示为（ ）A、1.55×107只 B、1.55×108只 C、0.155×109只 D、5×106只7. 化简 的结果是（ ）A、 B、 C、 D、8. 为了证明数轴上的点可以表示无理数，老师给学生设计了如下材料：如图，直径为1个单位长度的圆从原点沿数轴向右滚动一周，圆上一点由原点（记为点O）到达点A ， 点A对应的数是多少？从图中可以看出OA的长是这个圆的周长π，所以点A对应的数是π，这样，无理数π可以用数轴上的点表示出来，上述材料体现的数学思想是（ ）
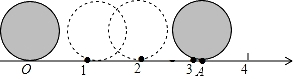A、方程思想 B、从特殊到一般 C、数形结合思想 D、分类思想9. 2019年女排世界杯于9月在日本举行，中国女排以十一连胜的骄人成绩卫冕冠军，充分展现了团队协作、顽强拼搏的女排精神．如图是某次比赛中垫球时的动作．若将垫球后排球的运动路线近似的看作抛物线，在同一竖直平面内建立如图所示的直角坐标系，已知运动员垫球时（图中点A）离球网的水平距离为5米，排球与地面的垂直距离为0.5米，排球在球网上端0.26米处（图中点B）越过球网（女子排球赛中球网上端距地面的高度为2.24米），落地时（图中点C）距球网的水平距离为2.5米，则排球运动路线的函数表达式为（ ）
A、y＝﹣ B、y＝﹣ C、y＝ D、y＝10. 如图，在Rt△ABC中，∠C＝90°，AB＝6，AD是∠BAC的平分线，经过A ， D两点的圆的圆心O恰好落在AB上，⊙O分别与A、B、AC相交于点E、F ． 若圆半径为2．则阴影部分面积（ ）
A、 B、 C、 D、二、填空题（共5小题，每小题3分，满分15分）
-
11. 计算： × ＝ ．12. 太谷饼是山西省传统名吃，以其香、酥、绵、软而闻名全国，某网店以a元一包的价格购进500包太谷饼，加价20%卖出400包以后，剩余每包比进价降低b元后全部卖出，则可获得利润元．
13. 如图，在△ABC中，AC＝BC ， 分别以点A和点C为圆心，大于 AC长为半径画弧，两弧相交于点M ， N ， 连接MN分别交BC、AC于点D、E ， 连接AD ． 若∠B＝70°，则∠BAD的度数是度．
14. 如图，在Rt△ABC中，∠BAC＝90°，点A的坐标（0，2），顶点C在反比例函数y＝ （x＞0）的图象上．若AB＝2AC ， 且OA＝OB ， 则k＝
15. 如图，将矩形纸片ABCD沿MN折叠，使点B与点D重合，再将△CDN沿DN折叠．使点C恰好落在MN上的点F处．若MN＝5，则AD的长为 ．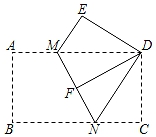
三、解答题（共8小题，满分75分）
-
16.
(1)、计算：（﹣ ）﹣2﹣|﹣5|+3cos45°﹣
(2)、解方程：x2+3＝3（x+1）17. 如图，在▱ABCD中，点E是BC上的一点，连接DE ， 在DE上取一点F使得∠AFE＝∠ADC ． 若DE＝AD ， 求证：DF＝CE ．
18. 2020年春节前夕“新型冠状病毒”爆发．疫情就是命令，防控就是使命．全国各地驰援武汉的医护工作者，践行医者仁心的使命与担当舍小家，为大家，用自己的专业知识与血肉之躯构筑起全社会抗击疫情的钢铁长城．下面是2月9日当天全国部分省市驰援武汉医护工作者的人数统计图（不完整）．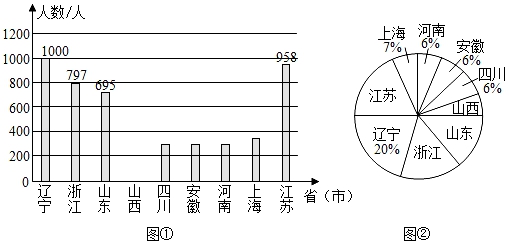
请解答下列问题：
(1)、①上述省市2月9日当天驰援武汉的医护工作者的总人数为人；②请将条形统计图补充完整；
(2)、请求出扇形统计图中“山西”所对应扇形的圆心角的度数；(3)、本次山西驰援武汉的医护工作者中，有5人报名去重症区，王医生和李医生就在其中，若从报名的5人中随机安排2人，求同时安排王医生和李医生的概率．19. 为更好地推进太原市生活垃圾分类工作，改善城市生态环境，2019年12月17日，太原市政府召开了太原市生活垃圾分类推进会，意味着太原垃圾分类战役的全面打响．某小区准备购买A ． B两种型号的垃圾箱，通过市场调研得知：购买3个A型垃圾箱和2个B型垃圾箱共雷540元，购买2个A型垃圾箱比购买3个B型垃圾箱少用160元．
(1)、求每个A型垃圾箱和B型垃圾箱各多少元？(2)、该小区物业计划用不多于2100元的资金购买A、B两种型号的垃圾箱共20个，则该小区最多可以购买B型垃圾箱多少个．20. 云岗石窟位于山西大同市，是中国规模最大的古代石窟群之一，位于第五窟的三世佛的中央坐像是云冈石窟最大的佛像．某数学课题研究小组针对“三世佛的中央坐像的高度有多少米“这一问题展开探究，过程如下：问题提出：
如图①是三世佛的中央坐像，请你设计方案并求出它的高度．
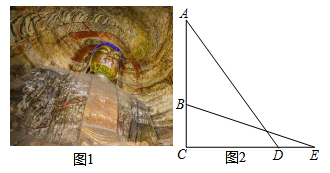
方案设计：
如图②，该课题研究小组通过研究设计了这样一个方案，某同学在D处用测角器测得佛像最高处A的仰角∠ADC＝40°，另一个同学在他的后方2.14m的E处测得佛像底端B的仰角∠BEC＝10°．
数据收集：
通过查阅资料和实际测量：佛像底端到观景台的垂直距离BC为5m ．
问题解决：
(1)、根据上述方案及数据，求佛像AB的高度；（结果保留整数，参考数据：sin10°≈0.17，cos10°≈0.98，tan10°≈0.18，sin40°≈＝0.64，cos40°≈0.77，tan40°≈＝0.84）(2)、在实际测量的过程中，有哪些措施可以减小测量数据产生的误差？（写出一条即可）21. 阅读下列材料，并完成相应任务：黄金分割
天文学家开普勒把黄金分割称为神圣分割，并指出毕达哥拉斯定理（勾股定理）和黄金分割是几何中的双宝，前者好比黄金，后者堪称珠宝，历史上最早正式在书中使用“黄金分割”这个名称的是欧姆，19世纪以后“黄金分割”的说法逐渐流行起来，黄金分割被广泛应用于建筑等领域．黄金分割指把一条线段分为两部分，使其中较长部分与线段总长之比等于较短部分与较长部分之比，该比值为 ，用下面的方法（如图①）就可以作出已知线段AB的黄金分割点H：
①以线段AB为边作正方形ABCD ，
②取AD的中点E ， 连接EB ，
③延长DA到F ， 使EF＝EB ，
④以线段AF为边作正方形AFGH ， 点H就是线段AB的黄金分割点．
以下是证明点H就是线段AB的黄金分割点的部分过程：
证明：设正方形ABCD的边长为1，则AB＝AD＝1，
∵E为AD中点，
∴AE＝ ，
∴在Rt△BAE中，BE＝
∵EF＝BE
∴EF＝
∴AF＝EF﹣AE＝ ，
…
任务：
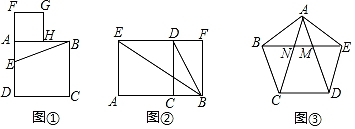(1)、补全题中的证明过程；(2)、如图②，点C为线段AB的黄金分割点，分别以AC、BC为边在线段AB同侧作正方形ACDE和矩形CBFD ， 连接BD、BE ． 求证：△EAB∽△BCD；(3)、如图③，在正五边形ABCDE中，对角线AD、AC与EB分别交于点M、N ， 求证：点M是AD的黄金分割点．22. 综合与实践问题情境
数学活动课上，老师让同学们以“三角形的旋转”为主题开展数学活动，△ABC和△DEC是两个全等的直角三角形纸片，其中∠ACB＝∠DCE＝90°，∠B＝∠E＝30°，AB＝DE＝4．
解决问题
(1)、如图①，智慧小组将△DEC绕点C顺时针旋转，发现当点D恰好落在AB边上时，DE∥AC ， 请你帮他们证明这个结论；(2)、缜密小组在智慧小组的基础上继续探究，连接AE、AD、BD ， 当△DEC绕点C继续旋转到如图②所示的位置时，他们提出S△BDC＝S△AEC ， 请你帮他们验证这一结论是否正确，并说明理由；探索发现
(3)、如图③，勤奋小组在前两个小组的启发下，继续旋转△DEC ， 当B、A、E三点共线时，求BD的长；(4)、在图①的基础上，写出一个边长比为1： ：2的三角形（可添加字母）23. 综合与探究如图，抛物线y＝﹣ +2x+6与x轴交于A、B两点（点A在点B的左侧），与y轴交于点C ， 连接BC ， 点D为抛物线对称轴上一动点．
(1)、求直线BC的函数表达式；(2)、连接OD ， CD ， 求△OCD周长的最小值；(3)、在抛物线上是否存在一点E ． 使以B、C、D、E为顶点的四边形是以BC为边的平行四边形？若存在，请直接写出E点的坐标；若不存在，请说明理由．