福建省三明市2020年中考数学三模考试试卷
试卷更新日期:2020-04-21 类型:中考模拟
一、选择题(共10小题)
-
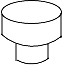
1. 在Rt△ABC中,∠C=90°,BC=4,AC=3,则cosA的值是( )A、 B、 C、 D、2. 下列运算正确是( )A、2a3+5a2=7a5 B、3 ﹣ =3 C、(﹣x2)•(﹣x3)=﹣x5 D、( m﹣n)(﹣ m﹣n)=n2﹣ m23. 如图所示的工件,其俯视图是( )
 A、
A、 B、
B、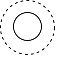 C、
C、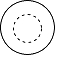 D、
D、 4. 某车间需加工一批零件,车间20名工人每天加工零件数如表所示:
4. 某车间需加工一批零件,车间20名工人每天加工零件数如表所示:每天加工零件数
4
5
6
7
8
人数
3
6
5
4
2
每天加工零件数的中位数和众数为( )
A、6,5 B、6,6 C、5,5 D、5,65. 如图,下列条件不能判定△ADB∽△ABC的是( )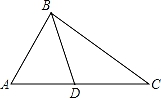 A、∠ABD=∠ACB B、∠ADB=∠ABC C、AB2=AD•AC D、 =6. 关于x的一元二次方程9x2﹣6x+k=0有两个不相等的实根,则k的范围是( )A、k<1 B、k>1 C、k≤1 D、k≥17. 反比例函数y= 和一次函数y=kx﹣k在同一直角坐标系中的图象大致是( )A、
A、∠ABD=∠ACB B、∠ADB=∠ABC C、AB2=AD•AC D、 =6. 关于x的一元二次方程9x2﹣6x+k=0有两个不相等的实根,则k的范围是( )A、k<1 B、k>1 C、k≤1 D、k≥17. 反比例函数y= 和一次函数y=kx﹣k在同一直角坐标系中的图象大致是( )A、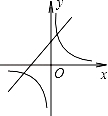 B、
B、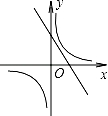 C、
C、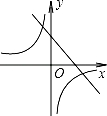 D、
D、 8. 如图,平行四边形ABCD中,M是BC的中点,且AM=9,BD=12,AD=10,则ABCD的面积是( )
8. 如图,平行四边形ABCD中,M是BC的中点,且AM=9,BD=12,AD=10,则ABCD的面积是( )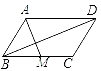 A、30 B、36 C、54 D、729. 受益于电子商务发展和法治环境改善等多重因素,“快递业”成为我国经济的一匹“黑马”,2016年我国快递业务量为300亿件,2018年快递量将达到450亿件,若设快递量平均每年增长率为x , 则下列方程中,正确是( )A、300(1+x)=450 B、300(1+2x)=450 C、300(1+x)2=450 D、450(1﹣x)2=30010. 反比例函数y= 与y= 在第一象限的图象如图所示,作一条平行于x轴的直线分别交双曲线于A、B两点,连接OA、OB , 则△AOB的面积为( )
A、30 B、36 C、54 D、729. 受益于电子商务发展和法治环境改善等多重因素,“快递业”成为我国经济的一匹“黑马”,2016年我国快递业务量为300亿件,2018年快递量将达到450亿件,若设快递量平均每年增长率为x , 则下列方程中,正确是( )A、300(1+x)=450 B、300(1+2x)=450 C、300(1+x)2=450 D、450(1﹣x)2=30010. 反比例函数y= 与y= 在第一象限的图象如图所示,作一条平行于x轴的直线分别交双曲线于A、B两点,连接OA、OB , 则△AOB的面积为( )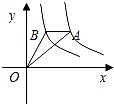 A、 B、2 C、3 D、1
A、 B、2 C、3 D、1二、填空题(共6小题)
-
11. 计算:2cos60°+tan45°= .12. 点D是线段AB的黄金分割点(AD>BD),若AB=2,则BD= .13. 如图,电灯P在横杆AB的正上方,AB在灯光下的影子为CD , AB∥CD , AB=2m , CD=6m , 点P到CD的距离为9m , 则AB与CD间的距离是m .
 14. 若关于x的一元二次方程x2+mx+m2﹣19=0的一个根是﹣3,则m的值是 .15. 如图,E , F是正方形ABCD的对角线AC上的两点,AC=8,AE=CF=2,则四边形BEDF的周长是 .
14. 若关于x的一元二次方程x2+mx+m2﹣19=0的一个根是﹣3,则m的值是 .15. 如图,E , F是正方形ABCD的对角线AC上的两点,AC=8,AE=CF=2,则四边形BEDF的周长是 .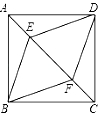 16. 如图,在Rt△ABC中,∠C=90°,AC=3,BC=4,点D是AB的中点,点P是直线BC上一点,将△BDP沿DP所在的直线翻折后,点B落在B1处,若B1D⊥BC , 则点P与点B之间的距离为 .
16. 如图,在Rt△ABC中,∠C=90°,AC=3,BC=4,点D是AB的中点,点P是直线BC上一点,将△BDP沿DP所在的直线翻折后,点B落在B1处,若B1D⊥BC , 则点P与点B之间的距离为 .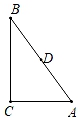
三、解答题
-
17. 计算:4cos30°﹣3tan60°+2sin45°•cos45°.18. 解方程:x(x﹣2)+x﹣2=0.19. 有甲、乙两个不透明的布袋,甲袋中有两个完全相同的小球,分别标有数字﹣1和3;乙袋中有三个完全相同的小球,分别标有数字1、0和﹣3.小丽先从甲袋中随机取出一个小球,记录下小球上的数字为x;再从乙袋中随机取出一个小球,记录下小球上的数字为y , 设点A的坐标为(x , y).(1)、请用表格或树状图列出点A所有可能的坐标;(2)、求点A在反比例函数y= 图象上的概率.20. 如图所示,点O是矩形ABCD对角线AC的中点,过点O作EF⊥AC , 交BC交于点E , 交AD于点F , 连接AE、CF , 求证:四边形AECF是菱形.
 21. 小明、小聪参加了100m跑的5期集训,每期集训结束时进行测试,根据他们的集训时间、测试成绩绘制成如下两个统计图。
21. 小明、小聪参加了100m跑的5期集训,每期集训结束时进行测试,根据他们的集训时间、测试成绩绘制成如下两个统计图。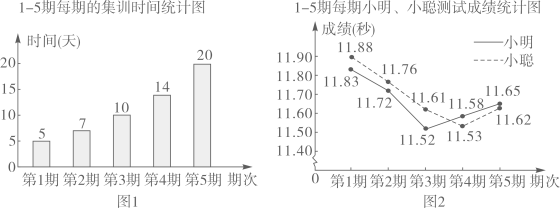
根据图中信息,解答下列问题:
(1)、这5期的集训共有多少天?小聪5次测试的平均成绩是多少?(2)、根据统计数据,结合体育运动的实际,从集训时间和测试成绩这两方面,说说你的想法.。22. 由我国完全自主设计、自主建造的首艘国产航母于2018年5月成功完成第一次海上试验任务.如图,航母由西向东航行,到达 处时,测得小岛 位于它的北偏东 方向,且与航母相距80海里再航行一段时间后到达 处,测得小岛 位于它的西北方向,求此时航母与小岛的距离 的长.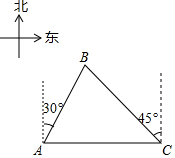 23. 某汽车专卖店经销某种型号的汽车.已知该型号汽车的进价为15万元/辆,经销一段时间后发现:当该型号汽车售价定为25万元/辆时,平均每周售出8辆;售价每降低0.5万元,平均每周多售出1辆.(1)、当售价为22万元/辆时,求平均每周的销售利润.(2)、若该店计划平均每周的销售利润是90万元,为了尽快减少库存,求每辆汽车的售价.24. 如图,一次函数y=k1x+b的图象与反比例函数y= 的图象相交于A、B两点,其中点A的坐标为(﹣1,4),点B的坐标为(4,n).
23. 某汽车专卖店经销某种型号的汽车.已知该型号汽车的进价为15万元/辆,经销一段时间后发现:当该型号汽车售价定为25万元/辆时,平均每周售出8辆;售价每降低0.5万元,平均每周多售出1辆.(1)、当售价为22万元/辆时,求平均每周的销售利润.(2)、若该店计划平均每周的销售利润是90万元,为了尽快减少库存,求每辆汽车的售价.24. 如图,一次函数y=k1x+b的图象与反比例函数y= 的图象相交于A、B两点,其中点A的坐标为(﹣1,4),点B的坐标为(4,n).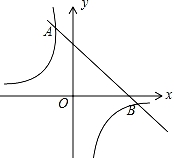 (1)、根据图象,直接写出满足k1x+b> 的x的取值范围;(2)、求这两个函数的表达式;(3)、点P在线段AB上,且S△AOP:S△BOP=1:2,求点P的坐标.25. 如图,在平面直角坐标系中,A、B两点的坐标分别为(20,0)和(0,15),动点P从点A出发在线段AO上以每秒2cm的速度向原点O运动,动直线EF从x轴开始以每秒lcm的速度向上平行移动(即EF∥x轴),分别与y轴、线段AB交于点E、F , 连接EP、FP , 设动点P与动直线EF同时出发,运动时间为t秒.
(1)、根据图象,直接写出满足k1x+b> 的x的取值范围;(2)、求这两个函数的表达式;(3)、点P在线段AB上,且S△AOP:S△BOP=1:2,求点P的坐标.25. 如图,在平面直角坐标系中,A、B两点的坐标分别为(20,0)和(0,15),动点P从点A出发在线段AO上以每秒2cm的速度向原点O运动,动直线EF从x轴开始以每秒lcm的速度向上平行移动(即EF∥x轴),分别与y轴、线段AB交于点E、F , 连接EP、FP , 设动点P与动直线EF同时出发,运动时间为t秒.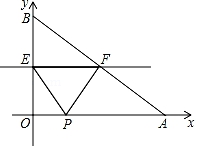 (1)、求t=9时,△PEF的面积;(2)、直线EF、点P在运动过程中,是否存在这样的t使得△PEF的面积等于40cm2?若存在,请求出此时t的值;若不存在,请说明理由;(3)、当t为何值时,△EOP与△BOA相似.
(1)、求t=9时,△PEF的面积;(2)、直线EF、点P在运动过程中,是否存在这样的t使得△PEF的面积等于40cm2?若存在,请求出此时t的值;若不存在,请说明理由;(3)、当t为何值时,△EOP与△BOA相似.