福建省漳州市2020年中考数学3月模拟考试试卷
试卷更新日期:2020-04-21 类型:中考模拟
一、选择题
-
1. 在下列四个实数中,最大的数是( )A、﹣ B、0 C、2﹣1 D、2. 如图所示的正六棱柱的主视图是( )
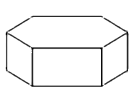 A、
A、 B、
B、 C、
C、 D、
D、 3. 下列计算正确是( )A、6a﹣3a=3 B、5y3•3y5=15y8 C、(a4b)3=a7b3 D、(a﹣5)2=a2﹣254. 下列图形中,既是轴对称图形,又是中心对称图形的是( )A、
3. 下列计算正确是( )A、6a﹣3a=3 B、5y3•3y5=15y8 C、(a4b)3=a7b3 D、(a﹣5)2=a2﹣254. 下列图形中,既是轴对称图形,又是中心对称图形的是( )A、 B、
B、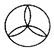 C、
C、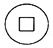 D、
D、 5. 古代数学名著《九章算术》有“米谷粒分”题:粮仓开仓收粮,有人送来米2018石,验得米内夹谷,抽样取米一把,数得270粒内夹谷30粒,则这批米内夹谷约为( )A、222石 B、224石 C、230石 D、232石6. 化简 + 的结果是( )A、x﹣2 B、 C、 D、7. 如图,五边形ABCDE和五边形A1B1C1D1E1是位似图形,点A和点A1是一对对应点,P是位似中心,且2PA=3PA1 , 则五边形ABCDE和五边形A1B1C1D1E1的相似比等于( )
5. 古代数学名著《九章算术》有“米谷粒分”题:粮仓开仓收粮,有人送来米2018石,验得米内夹谷,抽样取米一把,数得270粒内夹谷30粒,则这批米内夹谷约为( )A、222石 B、224石 C、230石 D、232石6. 化简 + 的结果是( )A、x﹣2 B、 C、 D、7. 如图,五边形ABCDE和五边形A1B1C1D1E1是位似图形,点A和点A1是一对对应点,P是位似中心,且2PA=3PA1 , 则五边形ABCDE和五边形A1B1C1D1E1的相似比等于( ) A、 B、 C、 D、8. 已知:将直线y=x﹣1向上平移2个单位长度后得到直线y=kx+b , 则下列关于直线y=kx+b的说法正确是( )A、经过第一、二、四象限 B、与x轴交于(1,0) C、与y轴交于(0,1) D、y随x的增大而减小9. 如图,在矩形ABCD中,AB=8,BC=4,将矩形沿AC折叠,则重叠部分△AFC的面积为( )
A、 B、 C、 D、8. 已知:将直线y=x﹣1向上平移2个单位长度后得到直线y=kx+b , 则下列关于直线y=kx+b的说法正确是( )A、经过第一、二、四象限 B、与x轴交于(1,0) C、与y轴交于(0,1) D、y随x的增大而减小9. 如图,在矩形ABCD中,AB=8,BC=4,将矩形沿AC折叠,则重叠部分△AFC的面积为( )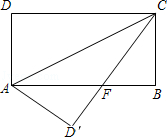 A、12 B、10 C、8 D、610. 如图,ABCD , DEFG都是正方形,边长分别为m , n(m>n),坐标原点O为AD的中点,A , D , G在y轴上,若反比例函数y= 的图象过C , F两点,则 =( )
A、12 B、10 C、8 D、610. 如图,ABCD , DEFG都是正方形,边长分别为m , n(m>n),坐标原点O为AD的中点,A , D , G在y轴上,若反比例函数y= 的图象过C , F两点,则 =( ) A、 B、 C、 D、 ﹣1
A、 B、 C、 D、 ﹣1二、填空题
-
11. 将数据4560000用科学记数法表示为 .12. 一只蚂蚁在如图所示的方格地板上随机爬行,每个小方格形状大小完全相同,当蚂蚁停下时,停在地板中阴影部分的概率为 .
 13. 如图,三角板的直角顶点落在矩形纸片的一边上.若∠1=35°,则∠2的度数是 .
13. 如图,三角板的直角顶点落在矩形纸片的一边上.若∠1=35°,则∠2的度数是 . 14. 如图,若一次函数y=﹣2x+b的图象与两坐标轴分别交于A , B两点,点A的坐标为(0,3),则不等式﹣2x+b>0的解集为 .
14. 如图,若一次函数y=﹣2x+b的图象与两坐标轴分别交于A , B两点,点A的坐标为(0,3),则不等式﹣2x+b>0的解集为 . 15. 观察下列等式:70=1,71=7,72=49,73=343,74=2401,75=16807,…,根据其中的规律可得70+71+72+…+72019的结果的个位数字是 .16. 如图,正方形ABCD中,AB=12,AE= AB , 点P在BC上运动(不与B , C重合),过点P作PQ⊥EP , 交CD于点Q , 求在点P运动的过程中,BP多长时,CQ有最大值,并求出最大值.
15. 观察下列等式:70=1,71=7,72=49,73=343,74=2401,75=16807,…,根据其中的规律可得70+71+72+…+72019的结果的个位数字是 .16. 如图,正方形ABCD中,AB=12,AE= AB , 点P在BC上运动(不与B , C重合),过点P作PQ⊥EP , 交CD于点Q , 求在点P运动的过程中,BP多长时,CQ有最大值,并求出最大值.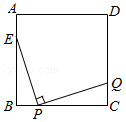
三、解答题(本大题共9小题,共86分.)
-
17. 解方程: .18. 如图,点E、F在BC上,BE=CF , AB=DC , ∠B=∠C , AF与DE交于点G , 求证:GE=GF .
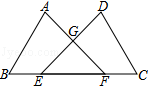 19. 解不等式组: ,并把解集在数轴是表示出来,并写出它的所有负整数解.
19. 解不等式组: ,并把解集在数轴是表示出来,并写出它的所有负整数解.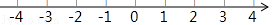 20. 在▱ABCD中,∠D=30°,AB<AD .
20. 在▱ABCD中,∠D=30°,AB<AD . (1)、在AD边上求作一点P , 使点P到边AB , BC的距离相等;(要求:尺规作图,不写作法,保留作图痕迹)(2)、在(1)的条件下,连接BP , 若AB=2,求△ABP的面积.21. 滴滴快车是一种便捷的出行工具,计价规则如下表:
(1)、在AD边上求作一点P , 使点P到边AB , BC的距离相等;(要求:尺规作图,不写作法,保留作图痕迹)(2)、在(1)的条件下,连接BP , 若AB=2,求△ABP的面积.21. 滴滴快车是一种便捷的出行工具,计价规则如下表:计费项目
里程费
时长费
远途费
单价
1.8元/公里
0.3元/分钟
0.8元/公里
注:车费由里程费、时长费、远途费三部分构成,其中里程费按行车的实际里程计算;时长费按行车的实际时间计算;远途费的收取方式为:行车里程7公里以内(含7公里)不收远途费,超过7公里的,超出部分每公里收0.8元.
小王与小张各自乘坐满滴快车,在同一地点约见,已知到达约见地点时他们的实际行车里程分别为6公里与8.5公里,两人付给滴滴快车的乘车费相同.
(1)、求这两辆滴滴快车的实际行车时间相差多少分钟;(2)、实际乘车时间较少的人,由于出发时间比另一人早,所以提前到达约见地点在大厅等候.已知他等候另一人的时间是他自己实际乘车时间的1.5倍,且比另一人的实际乘车时间的一半多8.5分钟,计算俩人各自的实际乘车时间.22. 在某旅游景区上山的一条小路上,有一些断断续续的台阶,下图是其中的甲、乙两段台阶的示意图,图中的数字表示每一级台阶的高度(单位:cm),请你用所学过的有关统计的知识回答下列问题(数据15,16,16,14,14,15的方差S甲2= ,数据11,15,18,17,10,19的方差S乙2= )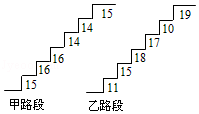 (1)、分别求甲、乙两段台阶路的高度平均数;(2)、哪段台阶路走起来更舒服?与哪个数据(平均数,中位数方差和极差)有关?(3)、为方便游客行走,需要重新整修上山的小路,对于这两段台阶路,在总高度及台阶数不变的情况下,请你提出合理的整修建议.23. 如图,在△ABC中,AB=AC= ,∠BAC=45°,将△ABC绕点A按顺时针方向旋转得到△AEF , 连接BE , CF相交于点D .
(1)、分别求甲、乙两段台阶路的高度平均数;(2)、哪段台阶路走起来更舒服?与哪个数据(平均数,中位数方差和极差)有关?(3)、为方便游客行走,需要重新整修上山的小路,对于这两段台阶路,在总高度及台阶数不变的情况下,请你提出合理的整修建议.23. 如图,在△ABC中,AB=AC= ,∠BAC=45°,将△ABC绕点A按顺时针方向旋转得到△AEF , 连接BE , CF相交于点D . (1)、求证:BE=CF;(2)、当四边形ACDE为菱形时,求BD的长.24. 在△ABC中,∠ABC=90°, =n , M是BC上一点,连接AM .
(1)、求证:BE=CF;(2)、当四边形ACDE为菱形时,求BD的长.24. 在△ABC中,∠ABC=90°, =n , M是BC上一点,连接AM .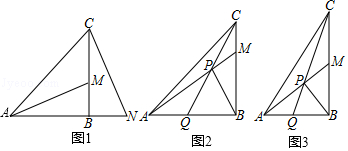 (1)、如图1,若n=1,N是AB延长线上一点,CN与AM垂直,求证:BM=BN .(2)、过点B作BP⊥AM , P为垂足,连接CP并延长交AB于点Q .
(1)、如图1,若n=1,N是AB延长线上一点,CN与AM垂直,求证:BM=BN .(2)、过点B作BP⊥AM , P为垂足,连接CP并延长交AB于点Q .①如图2,若n=1,求证: = .
②如图3,若M是BC的中点,直接写出tan∠BPQ的值.(用含n的式子表示)
25. 已知二次函数y=ax2+bx+c , 其中a>0.(1)、若方程ax2+bx+c+2x=0有两个实根x1=1,x2=3,且方程ax2+bx+c+6a=0有两个相等的实根,求二次函数的解析式;(2)、若二次函数y=ax2+bx+c的图象与x轴交于A(﹣3,0),B(m , 0)两点,且当﹣1≤x≤0时,ax2+bx+c≤0恒成立,求实数m的取值范围.