福建省福州市2020年中考数学一模考试试卷
试卷更新日期：2020-04-21 类型：中考模拟
一、选择题
-
1. 下列图形是中心对称图形而不是轴对称图形的是（ ）A、
B、
C、
D、
2. 下列事件中是必然事件的是（ ）A、从一个装有黄、白两色球的缸里摸出一个球，摸出的球是白球 B、小丹的自行车轮胎被钉子扎坏 C、小红期末考试数学成绩一定得满分 D、将豆油滴入水中，豆油会浮在水面上3. 如图，AB是⊙O的弦，OC⊥AB，交⊙O于点C，连接OA，OB，BC，若∠ABC＝20°，则∠AOB的度数是（ ）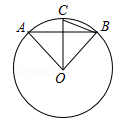
A、40° B、50° C、70° D、80°4. 已知点A（m ， n）在第二象限，则点B（|m|，﹣n）在（ ）A、第一象限 B、第二象限 C、第三象限 D、第四象限5. 如图，过⊙O上一点C作⊙O的切线，交⊙O直径AB的延长线于点D.若∠D＝40°，则∠A的度数为（ ）
A、20° B、25° C、30° D、40°6. 如图，在△ABC中，D、E分别为AB、AC边上的点，且∠AED＝∠B ， AD＝3，AC＝6，DB＝5，则AE的长度为（ ）
A、 B、 C、 D、47. 抛物线y＝ax2+bx﹣3与x轴交于A ， B两点，与y轴交于点C ， 且OB＝OC＝3OA ， 求抛物线的解析式（ ）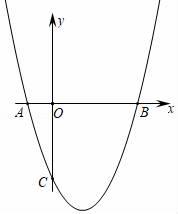
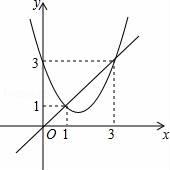
A、y＝x2﹣2x﹣3 B、y＝x2﹣2x+3 C、y＝x2﹣2x﹣4 D、y＝x2﹣2x﹣58.如图，在平面直角坐标系中，⊙M与x轴相切于点A（8，0），与y轴分别交于点B（0，4）和点C（0，16），则圆心M到坐标原点O的距离是（ ）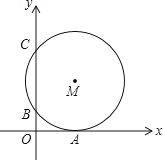
A、10 B、8 C、4 D、29. 函数y＝x2+bx+c与y＝x的图象如图所示，有以下结论：①b2﹣4c＞0；②b+c+1＝0；③3b+c+6＝0；④当1＜x＜3时，x2+（b﹣1）x+c＜0．其中正确个数为（ ）
A、1个 B、2个 C、3个 D、4个10. 已知四边形OABC是矩形，边OA在x轴上，边OC在y轴上，双曲线与边BC交于点D、与对角线OB交于点中点E ， 若△OBD的面积为10，则k的值是（ ）
A、10 B、5 C、 D、二、填空题
-
11. 若点A（2x﹣1，5）和点B（4，y+3）关于点（﹣3，2）对称，那么点A在第象限．12. 在1×2的正方形网格格点上放三枚棋子，按图所示的位置已放置了两枚棋子，若第三枚棋子随机放在其它格点上，则以这三枚棋子所在的格点为顶点的三角形是直角三角形的概率是 ．
13. 若抛物线的顶点坐标为（2，9），且它在x轴截得的线段长为6，则该抛物线的表达式为 ．14. 如图，在扇形AOB中，AC为弦，∠AOB＝130°，∠CAO＝60°，OA＝6，则 的长为 ．
15. 已知a2+a﹣3＝0，则a3+3a2﹣a+4的值为.16. 某农场拟建两间矩形饲养室，一面靠现有墙（墙足够长），中间用一道墙隔开，并在如图所示的三处各留1m宽的门．已知计划中的材料可建墙体（不包括门）总长为27m，则能建成的饲养室面积最大为 m2 ．
三、解答题（共9小题，共86分）
-
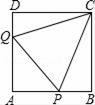
17. 解方程：x2+2x﹣2＝0．18. 关于x的一元二次方程（m﹣1）x2﹣2mx+m+1＝0有两个实数根，若方程的两个实数根都是正整数，求整数m的值．19. 如图，正方形ABCD的边长为1，AB ， AD上各有一点P ， Q ， 如果△APQ的周长为2，求∠PCQ的度数．
20. 如图，△ABC的三个顶点都在⊙O上，直径AD＝6cm ， ∠DAC＝2∠B ， 求AC的长．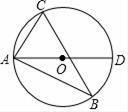
21. 若n是一个两位正整数，且n的个位数字大于十位数字，则称n为“两位递增数”（如13，35，56等）．在某次数学趣味活动中，每位参加者需从由数字1，2，3，4，5，6构成的所有的“两位递增数”中随机抽取1个数，且只能抽取一次．
(1)、写出所有个位数字是5的“两位递增数”；
(2)、请用列表法或树状图，求抽取的“两位递增数”的个位数字与十位数字之积能被10整除的概率．22. 如图，在平面直角坐标系xOy中，直线y＝x+1与双曲线y＝ 的一个交点为P（m，2）．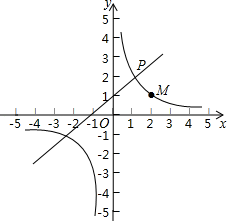
(1)、求k的值；(2)、M（ ，a），N（n，b）是双曲线上的两点，直接写出当a＞b时，n的取值范围．23. 在锐角△ABC中，边BC长为18，高AD长为12
(1)、如图，矩形EFCH的边GH在BC边上，其余两个顶点E、F分别在AB、AC边上，EF交AD于点K ， 求 的值；(2)、设EH＝x ， 矩形EFGH的面积为S ， 求S与x的函数关系式，并求S的最大值．24. 如图1，AB为⊙O的直径，C为⊙O上一点，连接CB ， 过C作CD⊥AB于点D ， 过点C作∠BCE ， 使∠BCE＝∠BCD ， 其中CE交AB的延长线于点E ．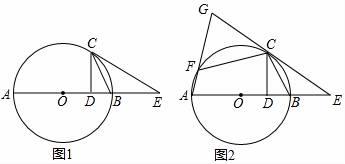
(1)、求证：CE是⊙O的切线．(2)、如图2，点F在⊙O上，且满足∠FCE＝2∠ABC ， 连接AF井延长交EC的延长线于点G ．①试探究线段CF与CD之间满足的数量关系；
②若CD＝4，BD＝2，求线段FG的长．
25. 综合与探究如图1，抛物线y＝ax2+bx﹣3与x轴交于A（﹣2，0），B（4，0）两点，与y轴交于点C ．
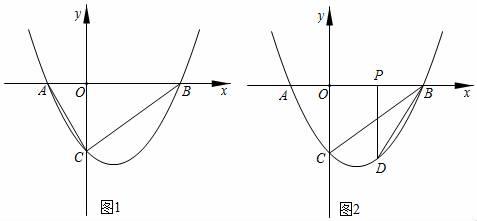(1)、求抛物线的表达式；(2)、点N是抛物线上异于点C的动点，若△NAB的面积与△CAB的面积相等，求出点N的坐标；(3)、如图2，当P为OB的中点时，过点P作PD⊥x轴，交抛物线于点D ． 连接BD ， 将△PBD沿x轴向左平移m个单位长度（0＜m≤2），将平移过程中△PBD与△OBC重叠部分的面积记为S ， 求S与m的函数关系式．