内蒙古赤峰市联盟校2019年中考数学三模考试试卷
试卷更新日期:2020-04-21 类型:中考模拟
一、选择题
-
1. 用配方法解方程x2+2x﹣3=0,下列配方结果正确是( )A、(x﹣1)2=2 B、(x﹣1)2=4 C、(x+1)2=2 D、(x+1)2=42. 关于x的一元二次方程 有实数根,则实数a满足( )A、a< B、a≥ C、a≤ 且a≠3 D、a≥ 且a≠33. 设x1 , x2是一元二次方程x2﹣2x﹣5=0的两根,则x12+x22的值为( )A、6 B、8 C、14 D、164. 在同一平面直角坐标系中,一次函数y=ax+b和二次函数y=ax2+bx+c的图象可能为( )A、
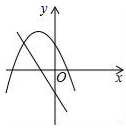 B、
B、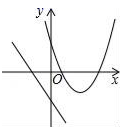 C、
C、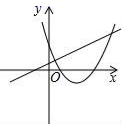 D、
D、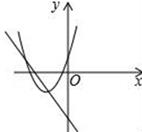 5. 在平面直角坐标系中,若将抛物线y=2x2﹣4x+3先向右平移3个单位长度,再向上平移2个单位长度,则经过这两次平移后所得抛物线的顶点坐标是( )A、(﹣2,3) B、(﹣1,4) C、(1,4) D、(4,3)6. 圆最长弦为12cm , 如果直线与圆相交,且直线与圆心的距离为d , 那么( )A、d<6cm B、6cm<d<12cm C、d≥6cm D、d>12cm7. 某地区2010年投入教育经费2500万元,预计到2012年共投入8000万元.设这两年投入教育经费的年平均增长率为x , 则下列方程正确是( )A、2500+2500(1+x)+2500(1+x)2=8000 B、2500x2=8000 C、2500(1+x)2=8000 D、2500(1+x)+2500(1+x)2=80008. 如图,直线AB与⊙O相切于点A , 弦CD∥AB , E , F为圆上的两点,且∠CDE=∠ADF . 若⊙O的半径为 ,CD=4,则弦EF的长为( )
5. 在平面直角坐标系中,若将抛物线y=2x2﹣4x+3先向右平移3个单位长度,再向上平移2个单位长度,则经过这两次平移后所得抛物线的顶点坐标是( )A、(﹣2,3) B、(﹣1,4) C、(1,4) D、(4,3)6. 圆最长弦为12cm , 如果直线与圆相交,且直线与圆心的距离为d , 那么( )A、d<6cm B、6cm<d<12cm C、d≥6cm D、d>12cm7. 某地区2010年投入教育经费2500万元,预计到2012年共投入8000万元.设这两年投入教育经费的年平均增长率为x , 则下列方程正确是( )A、2500+2500(1+x)+2500(1+x)2=8000 B、2500x2=8000 C、2500(1+x)2=8000 D、2500(1+x)+2500(1+x)2=80008. 如图,直线AB与⊙O相切于点A , 弦CD∥AB , E , F为圆上的两点,且∠CDE=∠ADF . 若⊙O的半径为 ,CD=4,则弦EF的长为( )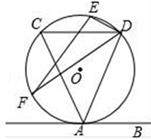 A、4 B、2 C、5 D、69. 如图,抛物线y=﹣x2+4x﹣3与x轴交于点A、B , 把抛物线在x轴及其上方的部分记作C1 , 将C1向右平移得C2 , C2与x轴交于点B , D . 若直线y=x+m与C1、C2共有3个不同的交点,则m的取值范围是( )
A、4 B、2 C、5 D、69. 如图,抛物线y=﹣x2+4x﹣3与x轴交于点A、B , 把抛物线在x轴及其上方的部分记作C1 , 将C1向右平移得C2 , C2与x轴交于点B , D . 若直线y=x+m与C1、C2共有3个不同的交点,则m的取值范围是( )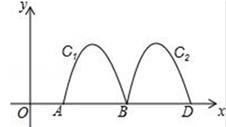 A、﹣3<m<﹣ B、﹣5<m<﹣ C、﹣5<m<﹣3 D、﹣3<m<﹣10. 以下命题的逆命题为真命题的是( )A、对顶角相等 B、同旁内角互补,两直线平行 C、若a=b , 则a2=b2 D、若a>0,b>0,则a2+b2>011. 在平面直角坐标系中,如果⊙O是以原点为圆心,以7为半径的圆,那么A(﹣3,4)与⊙O的位置关系是( )A、在⊙O外 B、在⊙O上 C、在⊙O内 D、不能确定12. 如图,四边形ABCD内接于⊙O , 点I是△ABC的内心,∠AIC=124°,点E在AD的延长线上,则∠CDE的度数为( )
A、﹣3<m<﹣ B、﹣5<m<﹣ C、﹣5<m<﹣3 D、﹣3<m<﹣10. 以下命题的逆命题为真命题的是( )A、对顶角相等 B、同旁内角互补,两直线平行 C、若a=b , 则a2=b2 D、若a>0,b>0,则a2+b2>011. 在平面直角坐标系中,如果⊙O是以原点为圆心,以7为半径的圆,那么A(﹣3,4)与⊙O的位置关系是( )A、在⊙O外 B、在⊙O上 C、在⊙O内 D、不能确定12. 如图,四边形ABCD内接于⊙O , 点I是△ABC的内心,∠AIC=124°,点E在AD的延长线上,则∠CDE的度数为( )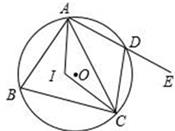 A、56° B、62° C、68° D、78°
A、56° B、62° C、68° D、78°二、填空题
-
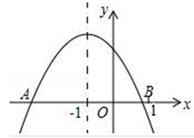
13. 在Rt△ABC中,∠ABC=90°,AB=6,BC=8,则这个三角形的外接圆的直径长为 .14. 用反证法证明“平行于同一条直线的两条直线互相平行”时,先假设成立,然后经过推理与平行公理相矛盾.15. 函数y=ax2﹣ax+3x+1的图象与x轴有且只有一个交点,那么a的值和交点坐标分别为 .16. 已知二次函数y=ax2+bx+c(a≠0)图象如图所示,现有下列结论,①abc>0; ②a+b+c<0;③b=2a;④a+b>0;则其中正确结论是(只填写序号).
 17. P为⊙O内一点,OP=3cm , ⊙O的半径为5cm , 则经过P点的最短弦长为cm , 最长弦长为cm .18. 如图,在平面鱼角坐标系xOy中,A(﹣3,0),点B为y轴正半轴上一点,将线段AB绕点B旋转90°至BC处,过点C作CD垂直x轴于点D,若四边形ABCD的面积为36,则线AC的解析式为.
17. P为⊙O内一点,OP=3cm , ⊙O的半径为5cm , 则经过P点的最短弦长为cm , 最长弦长为cm .18. 如图,在平面鱼角坐标系xOy中,A(﹣3,0),点B为y轴正半轴上一点,将线段AB绕点B旋转90°至BC处,过点C作CD垂直x轴于点D,若四边形ABCD的面积为36,则线AC的解析式为.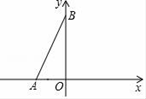
三、解答题(共8小题,满分96分)
-
19. 阅读下列材料:求函数y= 的最大值.
解:将原函数转化成关于x的一元二次方程,得(y﹣2)x2+(y﹣3)x+0.25y=0当y≠2时,∵x为实数,∴△=(y﹣3)2﹣4•(y﹣2)•0.25y=﹣4y+9≥0.
∴y≤ 且y≠2;
当y=2时,(y﹣2)x2+(y﹣3)x+0.25y=0即为﹣x+0.5=0,方程有解(x的值存在);
∴y≤ .因此,y的最大值为 .
根据材料给你的启示,求函数y= 的最小值.
20. 有一个二次函数满足以下条件:①函数图象与x轴的交点坐标分别为A(1,0),B(x2 , y2)(点B在点A的右侧);②对称轴是x=3;③该函数有最小值是﹣2.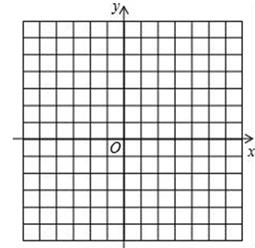 (1)、请根据以上信息求出二次函数表达式;(2)、将该函数图象中x>x2部分的图象向下翻折与原图象未翻折的部分组成图象“G”,试结合图象分析:平行于x轴的直线y=m与图象“G”的交点的个数情况.21. △ABC在方格纸中位置如图所示
(1)、请根据以上信息求出二次函数表达式;(2)、将该函数图象中x>x2部分的图象向下翻折与原图象未翻折的部分组成图象“G”,试结合图象分析:平行于x轴的直线y=m与图象“G”的交点的个数情况.21. △ABC在方格纸中位置如图所示 (1)、请在方格纸上建立平面直角坐标系,使得A、B两点的坐标分别为A(2,﹣1)、B(1,﹣4),并求出C点的坐标;(2)、作出△ABC关于横轴对称的△A1B1C1 , 再作出△ABC以坐标原点为旋转中心、旋转180°后的△A2B2C2 , 并写C1 , C2两点的坐标;(3)、观察△A1B1C1和△A2B2C2 , 其中的一个三角形能否由另一个三角形经过某种变换而得到?若能,请指出什么变换.22. 如图,⊙O直径AB和弦CD相交于点E , AE=2,EB=6,∠DEB=30°,求弦CD长.
(1)、请在方格纸上建立平面直角坐标系,使得A、B两点的坐标分别为A(2,﹣1)、B(1,﹣4),并求出C点的坐标;(2)、作出△ABC关于横轴对称的△A1B1C1 , 再作出△ABC以坐标原点为旋转中心、旋转180°后的△A2B2C2 , 并写C1 , C2两点的坐标;(3)、观察△A1B1C1和△A2B2C2 , 其中的一个三角形能否由另一个三角形经过某种变换而得到?若能,请指出什么变换.22. 如图,⊙O直径AB和弦CD相交于点E , AE=2,EB=6,∠DEB=30°,求弦CD长. 23. 如图,A是⊙O外一点,B为⊙O上一点,AO的延长线交⊙O于C点,连结BC , ∠C=22.5°,∠A=45°,求证:直线AB为⊙O切线.
23. 如图,A是⊙O外一点,B为⊙O上一点,AO的延长线交⊙O于C点,连结BC , ∠C=22.5°,∠A=45°,求证:直线AB为⊙O切线.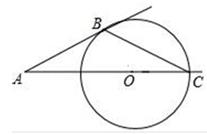 24. 如图,A城气象台测得台风中心在A城的正西方300千米处,以每小时10 千米的速度向北偏东60°的BF方向移动,距台风中心200千米的范围内是受这次台风影响的区域.
24. 如图,A城气象台测得台风中心在A城的正西方300千米处,以每小时10 千米的速度向北偏东60°的BF方向移动,距台风中心200千米的范围内是受这次台风影响的区域.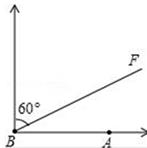 (1)、问A城是否会受到这次台风的影响?为什么?(2)、若A城受到这次台风的影响,那么A城遭受这次台风影响的时间有多长?25. 小明大学毕业回家乡创业,第一期培植盆景与花卉各50盆.售后统计,盆景的平均每盆利润是160元,花卉的平均每盆利润是19元.调研发现:
(1)、问A城是否会受到这次台风的影响?为什么?(2)、若A城受到这次台风的影响,那么A城遭受这次台风影响的时间有多长?25. 小明大学毕业回家乡创业,第一期培植盆景与花卉各50盆.售后统计,盆景的平均每盆利润是160元,花卉的平均每盆利润是19元.调研发现:①盆景每增加1盆,盆景的平均每盆利润减少2元;每减少1盆,盆景的平均每盆利润增加2元;
②花卉的平均每盆利润始终不变.
小明计划第二期培植盆景与花卉共100盆,设培植的盆景比第一期增加x盆,第二期盆景与花卉售完后的利润分别为W1 , W2(单位:元).
(1)、用含x的代数式分别表示W1 , W2;(2)、当x取何值时,第二期培植的盆景与花卉售完后获得的总利润W最大,最大总利润是多少?26. 已知抛物线y=﹣ x2﹣ x+2与x轴交于点A , B两点,交y轴于C点,抛物线的对称轴与x轴交于H点,分别以OC、OA为边作矩形AECO .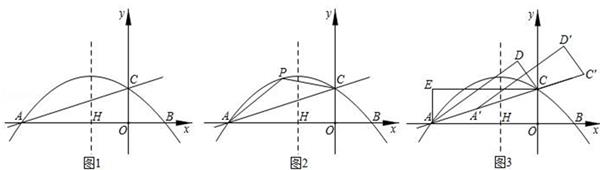 (1)、求直线AC的解析式;(2)、如图2,P为直线AC上方抛物线上的任意一点,在对称轴上有一动点M , 当四边形AOCP面积最大时,求|PM﹣OM|的值.(3)、如图3,将△AOC沿直线AC翻折得△ACD , 再将△ACD沿着直线AC平移得△A'C′D'.使得点A′、C'在直线AC上,是否存在这样的点D′,使得△A′ED′为直角三角形?若存在,请求出点D′的坐标;若不存在,请说明理由.
(1)、求直线AC的解析式;(2)、如图2,P为直线AC上方抛物线上的任意一点,在对称轴上有一动点M , 当四边形AOCP面积最大时,求|PM﹣OM|的值.(3)、如图3,将△AOC沿直线AC翻折得△ACD , 再将△ACD沿着直线AC平移得△A'C′D'.使得点A′、C'在直线AC上,是否存在这样的点D′,使得△A′ED′为直角三角形?若存在,请求出点D′的坐标;若不存在,请说明理由.