内蒙古赤峰市联盟校2019年中考数学二模考试试卷
试卷更新日期：2020-04-21 类型：中考模拟
一、选择题
-
1. 用配方法解方程x2﹣10x﹣1＝0，正确变形是（ ）A、（x﹣5）2＝1 B、（x+5）2＝26 C、（x﹣5）2＝26 D、（x﹣5）2＝242. 若关于x的一元二次方程kx2﹣6x+9＝0有两个不相等的实数根，则k的取值范围（ ）A、k＜1且k≠0 B、k≠0 C、k＜1 D、k＞13. 以2和4为根的一元二次方程是（ ）A、x2+6x+8＝0 B、x2﹣6x+8＝0 C、x2+6x﹣8＝0 D、x2﹣6x﹣8＝04. 当ab＞0时，y＝ax2与y＝ax＋b的图象大致是（ ）
A、
B、
C、
D、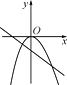
5. 将函数y＝x2的图象向左平移1个长度单位所得到的图象对应的函数关系式是（ ）A、y＝x2﹣1 B、y＝x2+1 C、y＝（x﹣1）2 D、y＝（x+1）26. 已知⊙O的半径为5cm ， 点A为直线L上一点，且OA＝5cm ， 则⊙O与L的位置关系是（ ）A、相交 B、相切 C、相切或相交 D、相离7. 某药品经过两次降价，每瓶零售价由168元降为108元，已知两次降价的百分率相同，设每次降价的百分率为x ， 根据题意列方程得（ ）A、168（1﹣x）2＝108 B、168（1﹣x2）＝108 C、168（1﹣2x）＝108 D、168（1+x）2＝1088. 用一把带有刻度的直角尺，①可以画出两条平行的直线a与b ， 如图（1）
②可以画出∠AOB的平分线OP ， 如图（2）
③可以检验工件的凹面是否成半圆，如图（3）
④可以量出一个圆的半径，如图（4）
上述四个方法中，正确个数是（ ）
A、4个 B、3个 C、2个 D、1个9. 如图，抛物线y＝﹣x2+4x﹣3与x轴交于点A、B ， 把抛物线在x轴及其上方的部分记作C1 ， 将C1向右平移得到C2 ， C2与x轴交于B、D两点．若直线y＝kx﹣k与C1、C2共有3个不同的交点，则k的最大值是（ ）
A、 B、2 ﹣6 C、6+4 D、6﹣410. 下列四个命题中，真命题有（ ）①两条直线被第三条直线所截，内错角相等．②如果∠1和∠2是对顶角，那么∠1＝∠2．③三角形的一个外角大于任何一个内角．④如果x2＞0，那么x＞0．
A、1个 B、2个 C、3个 D、4个11. 在平面直角坐标系xOy中，若点P（4，3）在⊙O内，则⊙O的半径r的取值范围是（ ）A、0＜r＜4 B、3＜r＜4 C、4＜r＜5 D、r＞512. 如图，△ABC的内切圆⊙O与AB ， BC ， CA分别相切于点D ， E ， F ， 且AD＝2，BC＝5，则△ABC的周长为（ ）
A、16 B、14 C、12 D、10二、填空题
-
13. 如图所示，⊙O是△ABC的外接圆，AD⊥BC于D ， 且AB＝5，AC＝4 ，AD＝4，则⊙O的直径的长度是 ．
14. 用反证法证明“三角形中最多有一个内角是直角”，应假设 ．15. 已知关于x的函数y=（m﹣1）x2+2x+m图象与坐标轴只有2个交点，则m=.16. 已知二次函数y＝ax2+bx+c的图象如图所示，对称轴为直线x＝﹣1，经过点（0，1）有以下结论：①a+b+c＜0；②b2﹣4ac＞0；③abc＞0；④4a﹣2b+c＜0；⑤c﹣a＞1，其中所有正确结论的序号是 ．
17. 如图，Rt△ABC中，AB⊥BC ， AB＝6，BC＝4，P是△ABC内部的一个动点，且满足∠PAB＝∠PBC ， 则线段CP长的最小值为 ．
18. 在平面直角坐标系中，点A（2，3）绕原点O逆时针旋转90°的对应点的坐标为 ．三、解答题（共8小题，满分96分）
-
19. 已知关于x的一元二次方程x2﹣（2k+1）x+k2+k＝0．(1)、求证：方程有两个不相等的实数根；(2)、当方程有一个根为1时，求k的值．20. 图中曲线是抛物线的一部分，我们建立平面直角坐标系如图所示，OA＝1.25，抛物线的最高点坐标为（1，2.25），
(1)、求图中曲线对应的函数关系式，直接写出自变量x的取值范围；(2)、图中曲线与x轴交点的坐标为；(3)、若抛物线形状不变，将其平移后仍过A点，且与x轴正半轴交于点B ， OB＝3.5，求平移后抛物线的最大高度是多少？21. 如图，在平面直角坐标系中，O为坐标原点，△ABC各顶点坐标分别为A（﹣2，3），B（﹣3，2），C（﹣1，1）
(1)、画出△ABC关于x轴的对称的图形△A1B1C1；(2)、将△ABC绕点C顺时针旋转90°得到△A2B2C ， 请在网格中画出△A2B2C ， 并直接写出线段A2C1的长．22. 已知：如图，在⊙O中，M是弧AB的中点，过点M的弦MN交弦AB于点C ， 设⊙O半径为4cm ， MN＝ cm ， OH⊥MN ， 垂足是点H ．
(1)、求OH的长度；(2)、求∠ACM的度数．23. 已知：AB是⊙O的直径，BD是⊙O的弦，延长BD到点C ， 使AB＝AC ， 连结AC ， 过点D作DE⊥AC ， 垂足为E ．
(1)、求证：DC＝BD；(2)、求证：DE为⊙O的切线．24. 如图，一艘轮船在位于灯塔P的北偏东30°方向，距离灯塔120海里的A处．轮船沿正南方向航行一段时间后，到达位于灯塔P的南偏东64°方向上的B处．求轮船所在的B处与灯塔P的距离．（结果精确到0.1海里）【参考数据：sin64°＝0.90，cos64°＝0.44，tan64°＝2.05】
25. 某商品的进价为每件50元．当售价为每件70元时，每星期可卖出300件，现需降价处理，且经市场调查：每降价1元，每星期可多卖出20件．在确保盈利的前提下，解答下列问题：
(1)、若设每件降价x元、每星期售出商品的利润为y元，请写出y与x的函数关系式，并求出自变量x的取值范围；
(2)、当降价多少元时，每星期的利润最大？最大利润是多少？26. 如图，直线y＝ x+a与x轴交于点A（4，0），与y轴交于点B ， 抛物线y＝ x2+bx+c经过点A ， B ． 点M（m ， 0）为x轴上一动点，过点M且垂直于x轴的直线分别交直线AB及抛物线于点P ， N ．
(1)、填空：点B的坐标为 ， 抛物线的解析式为；(2)、当点M在线段OA上运动时（不与点O ， A重合），①当m为何值时，线段PN最大值，并求出PN的最大值；
②求出使△BPN为直角三角形时m的值；
(3)、若抛物线上有且只有三个点N到直线AB的距离是h ， 请直接写出此时由点O ， B ， N ， P构成的四边形的面积．