内蒙古呼和浩特市2019年中考数学4月模拟考试试卷
试卷更新日期:2020-04-21 类型:中考模拟
一、选择题
-
1. 下列实数中,不是无理数的是( )A、2π(π表示圆周率) B、 C、 D、2. 以下调查中,用普查方式收集数据的是( )
①为了了解全校学生对任课教师的教学意见,学校向全校学生进行问卷调查;
②为了了解初中生上网情况,某市团委对10所初中学校的部分学生进行调查;
③某班学生拟组织一次春游活动,为了确定春游的地点,向全班同学进行调查;
④为了了解全班同学的作业完成情况,对学号为奇数的学生进行调查.
A、①③ B、①② C、②④ D、②③3. 一种原价均为m元的商品,甲超市连续两次打八折;乙超市一次性打六折;丙超市第一次打七折,第二次再打九折;若顾客要购买这种商品,最划算应到的超市是( )A、甲或乙或丙 B、乙 C、丙 D、乙或丙4. 如图所示,在平面直角坐标系中,点A、B、C的坐标分别为(﹣1,3)、(﹣4,1)、(﹣2,1),将△ABC沿一确定方向平移得到△A1B1C1 , 点B的对应点B1的坐标是(1,2),则点C对应的点C1的坐标是( )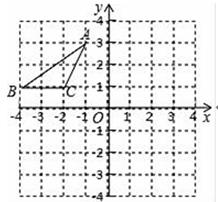 A、C1(3,2) B、C1(2,1) C、C1(2,3) D、C1(2,2)5. 下列各式在有意义情况下的变形中,正确是( )A、(﹣a2)3﹣5a3•a3=﹣4a6 B、2x2+3x4=5x6 C、 D、6. 由6个大小相同的正方体搭成的几何体,被小颖拿掉2个后,得到如图1所示的几何体,图2是原几何体的三视图.请你判断小颖拿掉的两个正方体原来放在( )
A、C1(3,2) B、C1(2,1) C、C1(2,3) D、C1(2,2)5. 下列各式在有意义情况下的变形中,正确是( )A、(﹣a2)3﹣5a3•a3=﹣4a6 B、2x2+3x4=5x6 C、 D、6. 由6个大小相同的正方体搭成的几何体,被小颖拿掉2个后,得到如图1所示的几何体,图2是原几何体的三视图.请你判断小颖拿掉的两个正方体原来放在( ) A、1号的前后 B、2号的前后 C、3号的前后 D、4号的左右7. 已知x1 , x2是关于x的方程x2+bx﹣3=0的两根,且满足x1+x2﹣3x1x2=4,那么b的值为( )A、5 B、﹣5 C、4 D、﹣48. 已知抛物线y=﹣3kx2+6kx+2(k>0)上有三点(﹣ ,y1)、( ,y2)、(3,y3),则( )A、y1<y2<y3 B、y1<y3<y2 C、y3<y2<y1 D、y2<y3<y19. 实数a、b、c、d在数轴上的位置如图所示,下列关系式不正确是( )
A、1号的前后 B、2号的前后 C、3号的前后 D、4号的左右7. 已知x1 , x2是关于x的方程x2+bx﹣3=0的两根,且满足x1+x2﹣3x1x2=4,那么b的值为( )A、5 B、﹣5 C、4 D、﹣48. 已知抛物线y=﹣3kx2+6kx+2(k>0)上有三点(﹣ ,y1)、( ,y2)、(3,y3),则( )A、y1<y2<y3 B、y1<y3<y2 C、y3<y2<y1 D、y2<y3<y19. 实数a、b、c、d在数轴上的位置如图所示,下列关系式不正确是( ) A、|a|>|b| B、|b﹣d|=|b|+|d| C、|a﹣c|=c﹣a D、|d﹣1|>|c﹣a|10. 如图1,点F从菱形ABCD的顶点A出发,沿A→D→B以1cm/s的速度匀速运动到点B,图2是点F运动时,△FBC的面积y(cm2)随时间x(s)变化的关系图象,则a的值为( )
A、|a|>|b| B、|b﹣d|=|b|+|d| C、|a﹣c|=c﹣a D、|d﹣1|>|c﹣a|10. 如图1,点F从菱形ABCD的顶点A出发,沿A→D→B以1cm/s的速度匀速运动到点B,图2是点F运动时,△FBC的面积y(cm2)随时间x(s)变化的关系图象,则a的值为( )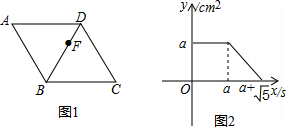 A、 B、2 C、 D、2
A、 B、2 C、 D、2二、填空题
-
11. 二元一次方程组 的解为 .12. 小明用公式S2= [(x1﹣3)2+(x2﹣3)2+…+(x10﹣3)2]计算一组数据x1 , x2 , …xn的方程,那么这组数据的和是 .13. 某中学组织的“红歌大赛”,60名选手的成绩统计如图,已知成续在94.5分以上的选手中男生和女生各占一半,学校从中随机确定2名参加市“红歌大赛”,则恰好选到一名男生和一名女生的概率为 .
 14. 分解因式:a3b﹣ab= .15. 如图,BD是⊙O的弦,点C在BD上,以BC为边作等边三角形△ABC , 点A在圆内,且AC恰好经过点O , 其中BC=12,OA=8,则BD的长为 .
14. 分解因式:a3b﹣ab= .15. 如图,BD是⊙O的弦,点C在BD上,以BC为边作等边三角形△ABC , 点A在圆内,且AC恰好经过点O , 其中BC=12,OA=8,则BD的长为 .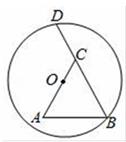 16. 我国古代伟大的数学家刘徽将勾股形(古人称直角三角形为勾股形)分割成一个正方形和两对全等的直角三角形,得到一个恒等式后人借助这种分割方法所得的图形证明了勾股定理如图所示的矩形由两个这样的图形拼成,若a=3,b=4,则该矩形的面积为 .
16. 我国古代伟大的数学家刘徽将勾股形(古人称直角三角形为勾股形)分割成一个正方形和两对全等的直角三角形,得到一个恒等式后人借助这种分割方法所得的图形证明了勾股定理如图所示的矩形由两个这样的图形拼成,若a=3,b=4,则该矩形的面积为 .
三、解答题
-
17.(1)、计算:(2)、解方程:18. 如图将矩形ABCD沿BD对折,点A落在E处,BE与CD相交于F .
 (1)、求证:△EDF≌△CBF;(2)、若AD=2,BD=4,求∠EBC的大小及CF的长.19. 某公司今年1月份的生产成本是400万元,由于改进技术,生产成本逐月下降,3月份的生产成本是361万元.假设该公司在1﹣6月份每个月生产成本的下降率都相同,请你预测4月份该公司的生产成本.20. 已知实数m是一个不等于2的常数,解不等式组 ,并根据m的取值情况写出其解集.21. 如图海中有一灯塔P , 它的周围8海里内有暗礁,海轮以18海里/时的速度由西向东航行,在A处测得灯塔P在北偏东58°方向上,航行40分钟到达B处,测得灯塔P在北偏东26°方向上.
(1)、求证:△EDF≌△CBF;(2)、若AD=2,BD=4,求∠EBC的大小及CF的长.19. 某公司今年1月份的生产成本是400万元,由于改进技术,生产成本逐月下降,3月份的生产成本是361万元.假设该公司在1﹣6月份每个月生产成本的下降率都相同,请你预测4月份该公司的生产成本.20. 已知实数m是一个不等于2的常数,解不等式组 ,并根据m的取值情况写出其解集.21. 如图海中有一灯塔P , 它的周围8海里内有暗礁,海轮以18海里/时的速度由西向东航行,在A处测得灯塔P在北偏东58°方向上,航行40分钟到达B处,测得灯塔P在北偏东26°方向上. (1)、求灯塔P到点B的距离;(2)、如果海轮不改变航线由B继续向东航行,通过计算估计海轮有没有触礁的危险?22. 某公司销售部统计了每个销售员一月份的销售额,绘制了如下折线统计图和扇形统计图:
(1)、求灯塔P到点B的距离;(2)、如果海轮不改变航线由B继续向东航行,通过计算估计海轮有没有触礁的危险?22. 某公司销售部统计了每个销售员一月份的销售额,绘制了如下折线统计图和扇形统计图:
设销售员的月销售额为x(单位:万元且x为整数),销售部规定当x<16时为“不称职”,当16≤x<20时为“基本称职”,当20≤x<25时为称职”,当x≥25时为“优秀”,根据以上信息解答下列问题:
(1)、计算销售部销售人员的总人数及销售额为26万元的人数并补全扇形统计图;(2)、求销售额达到称职及以上的所有销售员的月销售额的中位数和众数;(3)、为了调动销售员的积极性,销售部决定制定一个月销售额奖标准,如果欲使达到“称职和“优秀”的销售员中能有约一半人员获得奖励,月销售额奖励标准应定为多少万元(结果取整数)?并简述理由23. 如图,在平面直角坐标系xOy中,矩形OABC的顶点A在x轴上,顶点C在y轴上,D是BC的中点,过点D的反比例函数图象交AB于E点,连接DE , 若OD=5,OC=3. (1)、求过点D的反比例函数的解析式及DE所在直线的函数解析式;(2)、设直线DE与x轴和y轴的交点分别为M、N , 求△CMN的面积.24. 如图,AB是⊙O的直径,点E为线段OB上一点(不与O、B重合),作EC⊥OB , 交⊙O于点C , 作直径CD , 过点C的切线交DB的延长线于点P , 作AF⊥PC于点F , 连接CB .
(1)、求过点D的反比例函数的解析式及DE所在直线的函数解析式;(2)、设直线DE与x轴和y轴的交点分别为M、N , 求△CMN的面积.24. 如图,AB是⊙O的直径,点E为线段OB上一点(不与O、B重合),作EC⊥OB , 交⊙O于点C , 作直径CD , 过点C的切线交DB的延长线于点P , 作AF⊥PC于点F , 连接CB .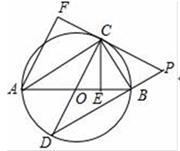 (1)、求证:AC平分∠FAB;(2)、求证:BC2=CE•CP;(3)、若 ,⊙O的面积为12π,求PF的长.25. 已知等式 y﹣ ax2+2a﹣1=0(1)、若等式中,已知a是非零常量,请写出因变量y与自变量x的函数解析式;当﹣1≤x≤3时,求y的最大值和最小值及对应的x的取值;(2)、若等式中,x是非零常量,请写出因变量y与自变量a的函数解析式,并判断x在什么范围内取值时,y随a的增大而增大.
(1)、求证:AC平分∠FAB;(2)、求证:BC2=CE•CP;(3)、若 ,⊙O的面积为12π,求PF的长.25. 已知等式 y﹣ ax2+2a﹣1=0(1)、若等式中,已知a是非零常量,请写出因变量y与自变量x的函数解析式;当﹣1≤x≤3时,求y的最大值和最小值及对应的x的取值;(2)、若等式中,x是非零常量,请写出因变量y与自变量a的函数解析式,并判断x在什么范围内取值时,y随a的增大而增大.