河北省唐山市滦南县2019年中考数学一模考试试卷
试卷更新日期:2020-04-21 类型:中考模拟
一、选择题
-
1. 下列运算结果正确是( )A、﹣3﹣(﹣2)=﹣5 B、(﹣3)2=﹣9 C、﹣5+2=﹣7 D、 ×5=2. 用三角板作△ABC的边BC上的高,下列三角板的摆放位置正确是( )A、
 B、
B、 C、
C、 D、
D、 3. 某校组织学生参观绿博园时,了解到某种花的花粉颗粒的直径大约为0.0000065米.将0.0000065用科学记数法表示为a×10n的形式,其中n的值为( )A、﹣6 B、6 C、﹣5 D、﹣74. 小明在校园艺术节上展示了自己创作的四幅作品,它们分别代表“立春”、“芒种”、“白露”、“大雪”,其中是轴对称图形的是( )A、
3. 某校组织学生参观绿博园时,了解到某种花的花粉颗粒的直径大约为0.0000065米.将0.0000065用科学记数法表示为a×10n的形式,其中n的值为( )A、﹣6 B、6 C、﹣5 D、﹣74. 小明在校园艺术节上展示了自己创作的四幅作品,它们分别代表“立春”、“芒种”、“白露”、“大雪”,其中是轴对称图形的是( )A、 B、
B、 C、
C、 D、
D、 5. 实数a , b在数轴上的位置如图所示,以下说法正确是( )
5. 实数a , b在数轴上的位置如图所示,以下说法正确是( ) A、a>b B、|a|>|b| C、a+b>0 D、ab>06. 某住宅小区六月份1日至5日每天用水量变化情况如图所示.那么这5天用水量的中位数是( )
A、a>b B、|a|>|b| C、a+b>0 D、ab>06. 某住宅小区六月份1日至5日每天用水量变化情况如图所示.那么这5天用水量的中位数是( )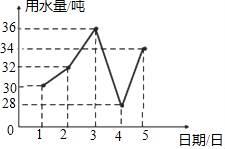 A、30吨 B、36吨 C、32吨 D、34吨7. 如图所示的几何体,它的俯视图是( )
A、30吨 B、36吨 C、32吨 D、34吨7. 如图所示的几何体,它的俯视图是( )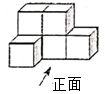 A、
A、 B、
B、 C、
C、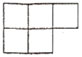 D、
D、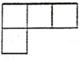 8. 如图,A处有一艘轮船,B处有一盏灯塔,则在轮船A处看灯塔B的方向是( )
8. 如图,A处有一艘轮船,B处有一盏灯塔,则在轮船A处看灯塔B的方向是( ) A、南偏东60° B、南偏东30° C、西偏北30° D、北偏西60°9. 定义一种新运算:a※b= ,则2※3﹣4※3的值( )A、5 B、8 C、7 D、610. 如图,圆上有两点A , B , 连接AB , 分别以A , B为圆心,AB的长为半径画弧,两弧相交于点C , D , CD交AB于点E , 交 于点F . 若EF=1,AB=6,则该圆的半径长是( )
A、南偏东60° B、南偏东30° C、西偏北30° D、北偏西60°9. 定义一种新运算:a※b= ,则2※3﹣4※3的值( )A、5 B、8 C、7 D、610. 如图,圆上有两点A , B , 连接AB , 分别以A , B为圆心,AB的长为半径画弧,两弧相交于点C , D , CD交AB于点E , 交 于点F . 若EF=1,AB=6,则该圆的半径长是( ) A、4 B、5 C、6 D、1011. 下列运算正确是( )A、x2+x2=x4 B、 a2•a3=a5 C、(3x)2 =6x2 D、(mn)5÷(mn)=mn412. 今年苹果的价格比去年便宜了20%,已知去年苹果的价格是每千克a元,则今年苹果每千克的价格是( )A、 B、 C、20%a D、(1﹣20%)a13. 若k< <k+1(k是整数),则k的值为( )A、6 B、7 C、8 D、914. 已知:△ABC中,AB=AC , 求证:∠B<90°,下面写出可运用反证法证明这个命题的四个步骤:
A、4 B、5 C、6 D、1011. 下列运算正确是( )A、x2+x2=x4 B、 a2•a3=a5 C、(3x)2 =6x2 D、(mn)5÷(mn)=mn412. 今年苹果的价格比去年便宜了20%,已知去年苹果的价格是每千克a元,则今年苹果每千克的价格是( )A、 B、 C、20%a D、(1﹣20%)a13. 若k< <k+1(k是整数),则k的值为( )A、6 B、7 C、8 D、914. 已知:△ABC中,AB=AC , 求证:∠B<90°,下面写出可运用反证法证明这个命题的四个步骤:①∴∠A+∠B+∠C>180°,这与三角形内角和为180°矛盾②因此假设不成立.∴∠B<90°③假设在△ABC中,∠B≥90°④由AB=AC , 得∠B=∠C≥90°,即∠B+∠C≥180°.这四个步骤正确顺序应是( )
A、③④①② B、③④②① C、①②③④ D、④③①②15. 如图,正比例函数y=x与反比例函数y= 的图象交于A、B两点,其中A(2,2),当y=x的函数值大于y= 的函数值时,x的取值范围( ) A、x>2 B、x<﹣2 C、﹣2<x<0或0<x<2 D、﹣2<x<0或x>216. 如图,若干个全等的正五边形排成环状,图中所示的是前3个正五边形,要完成这一圆环还需正五边形的个数为( )
A、x>2 B、x<﹣2 C、﹣2<x<0或0<x<2 D、﹣2<x<0或x>216. 如图,若干个全等的正五边形排成环状,图中所示的是前3个正五边形,要完成这一圆环还需正五边形的个数为( )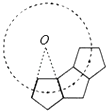 A、10 B、9 C、8 D、7
A、10 B、9 C、8 D、7二、填空题
-
17. 化简(﹣ )2+|1﹣ |+ 的结果为 .18. 在△ABC中,点E,F分别是边AB,AC的中点,点D在BC边上,连接DE,DF,EF,请你添加一个条件 , 使△BED与△FDE全等.
 19. 如图,在四边形ABCD中,AB∥DC , E是AD中点,EF⊥BC于点F , BC=5,EF=3.
19. 如图,在四边形ABCD中,AB∥DC , E是AD中点,EF⊥BC于点F , BC=5,EF=3. (1)、若AB=DC , 则四边形ABCD的面积S=;(2)、若AB>DC , 则此时四边形ABCD的面积S′S(用“>”或“=”或“<”填空).
(1)、若AB=DC , 则四边形ABCD的面积S=;(2)、若AB>DC , 则此时四边形ABCD的面积S′S(用“>”或“=”或“<”填空).三、解答题
-
20. 在解决问题“已知a= ,求2a2﹣8a+1的值”时,小明是这样分析与解答的:
∵a= = =2
∴a﹣2=﹣ ,∴(a﹣2)2=3,a2﹣4a+4=3
∴a2﹣4a=﹣1,∴2a2﹣8a+1=2(a2﹣4a)+1=2×(﹣1)+1=﹣1.
请你根据小明的分析过程,解决如下问题:
(1)、化简:(2)、若a= ,求3a2﹣6a﹣1的值.21. 某中学对本校初2017届500名学生中中考参加体育加试测试情况进行调查,根据男生1000米及女生800米测试成绩整理,绘制成不完整的统计图,(图①,图②),根据统计图提供的信息,回答问题: (1)、该校毕业生中男生有人;扇形统计图中a=;(2)、补全条形统计图;扇形统计图中,成绩为10分的所在扇形的圆心角是度;(3)、若500名学生中随机抽取一名学生,这名学生该项成绩在8分及8分以下的概率是多少?22. 已知C为线段AB上一点,关于x的两个方程 (x+1)=m与 (x+m)=m的解分别为线段AC , BC的长,(1)、当m=2时,求线段AB的长;(2)、若C为线段AB的三等分点,求m的值.23. 如图,已知AB是⊙O的直径,C为圆上一点,D是 的中点,CH⊥AB于H , 垂足为H , 联OD交弦BC于E , 交CH于F , 联结EH .
(1)、该校毕业生中男生有人;扇形统计图中a=;(2)、补全条形统计图;扇形统计图中,成绩为10分的所在扇形的圆心角是度;(3)、若500名学生中随机抽取一名学生,这名学生该项成绩在8分及8分以下的概率是多少?22. 已知C为线段AB上一点,关于x的两个方程 (x+1)=m与 (x+m)=m的解分别为线段AC , BC的长,(1)、当m=2时,求线段AB的长;(2)、若C为线段AB的三等分点,求m的值.23. 如图,已知AB是⊙O的直径,C为圆上一点,D是 的中点,CH⊥AB于H , 垂足为H , 联OD交弦BC于E , 交CH于F , 联结EH . (1)、求证:△BHE∽△BCO .(2)、若OC=4,BH=1,求EH的长.24. 如图,在平面直角坐标系中,直线y=x+2与x轴,y轴分别交于A,B两点,点C(2,m)为直线y=x+2上一点,直线y=﹣ x+b过点C.
(1)、求证:△BHE∽△BCO .(2)、若OC=4,BH=1,求EH的长.24. 如图,在平面直角坐标系中,直线y=x+2与x轴,y轴分别交于A,B两点,点C(2,m)为直线y=x+2上一点,直线y=﹣ x+b过点C.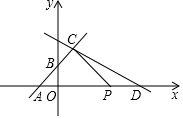 (1)、求m和b的值;(2)、直线y=﹣ x+b与x轴交于点D,动点P从点D开始以每秒1个单位的速度向x轴负方向运动.设点P的运动时间为t秒.
(1)、求m和b的值;(2)、直线y=﹣ x+b与x轴交于点D,动点P从点D开始以每秒1个单位的速度向x轴负方向运动.设点P的运动时间为t秒.①若点P在线段DA上,且△ACP的面积为10,求t的值;
②是否存在t的值,使△ACP为等腰三角形?若存在,直接写出t的值;若不存在,请说明理由.
25. 随着人们生活水平的提高,短途旅行日趋火爆.我市某旅行社推出“辽阳﹣葫芦岛海滨观光一日游”项目,团队人均报名费用y(元)与团队报名人数x(人)之间的函数关系如图所示,旅行社规定团队人均报名费用不能低于88元.旅行社收到的团队总报名费用为w(元) (1)、直接写出当x≥20时,y与x之间的函数关系式及自变量x的取值范围;(2)、儿童节当天旅行社收到某个团队的总报名费为3000元,报名旅游的人数是多少?(3)、当一个团队有多少人报名时,旅行社收到的总报名费最多?最多总报名费是多少元?26. 已知Rt△OAB , ∠OAB=90°,∠ABO=30°,斜边OB=4,将Rt△OAB绕点O顺时针旋转60°,如图1,连接BC .
(1)、直接写出当x≥20时,y与x之间的函数关系式及自变量x的取值范围;(2)、儿童节当天旅行社收到某个团队的总报名费为3000元,报名旅游的人数是多少?(3)、当一个团队有多少人报名时,旅行社收到的总报名费最多?最多总报名费是多少元?26. 已知Rt△OAB , ∠OAB=90°,∠ABO=30°,斜边OB=4,将Rt△OAB绕点O顺时针旋转60°,如图1,连接BC . (1)、填空:∠OBC=°;(2)、如图1,连接AC , 作OP⊥AC , 垂足为P , 求OP的长度;(3)、如图2,点M , N同时从点O出发,在△OCB边上运动,M沿O→C→B路径匀速运动,N沿O→B→C路径匀速运动,当两点相遇时运动停止,已知点M的运动速度为1.5单位/秒,点N的运动速度为1单位/秒,设运动时间为x秒,△OMN的面积为y , 求当x为何值时y取得最大值?最大值为多少?
(1)、填空:∠OBC=°;(2)、如图1,连接AC , 作OP⊥AC , 垂足为P , 求OP的长度;(3)、如图2,点M , N同时从点O出发,在△OCB边上运动,M沿O→C→B路径匀速运动,N沿O→B→C路径匀速运动,当两点相遇时运动停止,已知点M的运动速度为1.5单位/秒,点N的运动速度为1单位/秒,设运动时间为x秒,△OMN的面积为y , 求当x为何值时y取得最大值?最大值为多少?