河北省唐山市路北区2019年中考数学一模考试试卷
试卷更新日期:2020-04-21 类型:中考模拟
一、选择题
-
1. 计算 15÷(﹣3)的结果等于( )A、﹣5 B、5 C、﹣ D、2. 若代数式 在实数范围内有意义,则x的取值范围是( )A、x>2 B、x<2 C、x≠﹣2 D、x≠23. 下列四个实数中,比5小的是( )A、 ﹣1 B、 C、 ﹣1 D、4. 如图,直线AB∥CD , 则下列结论正确是( )
 A、∠1=∠2 B、∠3=∠4 C、∠1+∠3=180° D、∠3+∠4=180°5. 下列因式分解正确是( )A、x2+1=(x+1)2 B、x2+2x﹣1=(x﹣1)2 C、2x2﹣2=2(x+1)(x﹣1) D、x2﹣x+2=x(x﹣1)+26. 如图,一个可以自由转动的转盘被等分成6个扇形区域,并涂上了相应的颜色,转动转盘,转盘停止后,指针指向蓝色区域的概率是( )
A、∠1=∠2 B、∠3=∠4 C、∠1+∠3=180° D、∠3+∠4=180°5. 下列因式分解正确是( )A、x2+1=(x+1)2 B、x2+2x﹣1=(x﹣1)2 C、2x2﹣2=2(x+1)(x﹣1) D、x2﹣x+2=x(x﹣1)+26. 如图,一个可以自由转动的转盘被等分成6个扇形区域,并涂上了相应的颜色,转动转盘,转盘停止后,指针指向蓝色区域的概率是( ) A、 B、 C、 D、7. 解分式方程 ,分以下四步,其中,不正确一步是( )A、方程两边分式的最简公分母是(x﹣1)(x+1) B、方程两边都乘以(x﹣1)(x+1),得整式方程2(x﹣1)+3(x+1)=6 C、解这个整式方程,得x=1 D、原方程的解为x=18. 已知点A , 点B都在直线l的上方,试用尺规作图在直线l上求作一点P , 使得PA+PB的值最小,则下列作法正确是( )A、
A、 B、 C、 D、7. 解分式方程 ,分以下四步,其中,不正确一步是( )A、方程两边分式的最简公分母是(x﹣1)(x+1) B、方程两边都乘以(x﹣1)(x+1),得整式方程2(x﹣1)+3(x+1)=6 C、解这个整式方程,得x=1 D、原方程的解为x=18. 已知点A , 点B都在直线l的上方,试用尺规作图在直线l上求作一点P , 使得PA+PB的值最小,则下列作法正确是( )A、 B、
B、 C、
C、 D、
D、 9. 如图,∠ECB=80°,∠A=38°,将直线BC绕点C按逆时针方向旋转α(0°<α<180°),得到直线l , 若l∥AB , 则α等于( )
9. 如图,∠ECB=80°,∠A=38°,将直线BC绕点C按逆时针方向旋转α(0°<α<180°),得到直线l , 若l∥AB , 则α等于( ) A、38° B、42° C、80° D、132°10. 如果边长相等的正五边形和正方形的一边重合,那么∠1的度数是多少( )
A、38° B、42° C、80° D、132°10. 如果边长相等的正五边形和正方形的一边重合,那么∠1的度数是多少( )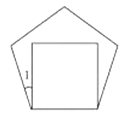 A、30° B、15° C、18° D、20°11. 已知点P(m , n),为是反比例函数y=﹣ 图象上一点,当﹣3≤n<﹣1时,m的取值范围是( )A、1≤m<3 B、﹣3≤m<﹣1 C、1<m≤3 D、﹣3<m≤﹣112. 有这样一道题:如图,在正方形ABCD中,有一个小正方形EFGH , 其中E , F , G分别在AB , BC , FD上,连接DH , 如果BC=12,BF=3.求tan∠HDG的值.以下是排乱的证明步骤:
A、30° B、15° C、18° D、20°11. 已知点P(m , n),为是反比例函数y=﹣ 图象上一点,当﹣3≤n<﹣1时,m的取值范围是( )A、1≤m<3 B、﹣3≤m<﹣1 C、1<m≤3 D、﹣3<m≤﹣112. 有这样一道题:如图,在正方形ABCD中,有一个小正方形EFGH , 其中E , F , G分别在AB , BC , FD上,连接DH , 如果BC=12,BF=3.求tan∠HDG的值.以下是排乱的证明步骤:①求出EF、DF的长;②求出tan∠HDG的值;③证明∠BFE=∠CDF;④求出HG、DG;⑤证明△BEF∽△CFD . 证明步骤正确顺序是( )
 A、③⑤①④② B、①④⑤③② C、③⑤④①② D、⑤①④③②13. 用半径为8的半圆围成一个圆锥的侧面,则圆锥的底面半径等于( )A、4 B、6 C、16π D、814. 某药品经过两次降价,每瓶零售价由168元降为108元,已知两次降价的百分率相同.设每次降价的百分率为x , 根据题意列方程得( )A、168(1+x)2=108 B、168(1﹣x)2=108 C、168(1﹣2x)=108 D、168y=x2(1﹣x2)=10815. 已知函数:①y=2x;②y=﹣ (x<0);③y=3﹣2x;④y=2x2+x(x≥0),其中,y随x增大而增大的函数有( )A、1个 B、2个 C、3个 D、4个16.
A、③⑤①④② B、①④⑤③② C、③⑤④①② D、⑤①④③②13. 用半径为8的半圆围成一个圆锥的侧面,则圆锥的底面半径等于( )A、4 B、6 C、16π D、814. 某药品经过两次降价,每瓶零售价由168元降为108元,已知两次降价的百分率相同.设每次降价的百分率为x , 根据题意列方程得( )A、168(1+x)2=108 B、168(1﹣x)2=108 C、168(1﹣2x)=108 D、168y=x2(1﹣x2)=10815. 已知函数:①y=2x;②y=﹣ (x<0);③y=3﹣2x;④y=2x2+x(x≥0),其中,y随x增大而增大的函数有( )A、1个 B、2个 C、3个 D、4个16.如图,在边长为2的正方形ABCD中剪去一个边长为1的小正方形CEFG,动点P从点A出发,沿A→D→E→F→G→B的路线绕多边形的边匀速运动到点B时停止(不含点A和点B),则△ABP的面积S随着时间t变化的函数图象大致是( )
 A、
A、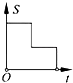 B、
B、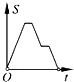 C、
C、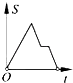 D、
D、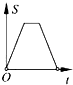
二、填空题
-
17. 计算 的结果是 .18. 如图,四边形ABCD与四边形EFGH位似,位似中心点是点O , ,则 = .
 19. 如图,过点A1(1,0)作x轴的垂线,交直线y=2x于点B1;点A2与点O关于直线A1B1对称;过点A₂(2,0)作x轴的垂线,交直线y=2x于点B2;点A3与点O关于直线A2B2对称;过点A3(4,0)作x轴的垂线,交直线y=2x于点B3;…,按此规律作下去,则
19. 如图,过点A1(1,0)作x轴的垂线,交直线y=2x于点B1;点A2与点O关于直线A1B1对称;过点A₂(2,0)作x轴的垂线,交直线y=2x于点B2;点A3与点O关于直线A2B2对称;过点A3(4,0)作x轴的垂线,交直线y=2x于点B3;…,按此规律作下去,则 (1)、点B4的坐标为 .(2)、点Bn的坐标为 .
(1)、点B4的坐标为 .(2)、点Bn的坐标为 .三、解答题(本大题共7个小题;共66分)
-
20. 定义新运算:a⊗b=a(1﹣b),其中等号右边是常规的乘法和减法运算,例如:(﹣1)⊗1=(﹣1)×(1﹣1)=0.(1)、计算:(1+ )⊗ ;(2)、嘉淇说:若a+b=0,则a⊗a+b⊗b=2ab , 你是否同意他的观点,请说明理由.21. 如图,平面内有公共端点的六条射线OA , OB , OC , OD , OE , OF , 从射线OA开始按逆时针方向依次在射线上写出数字1,2,3,4,5,6,7,…
 (1)、“17”在射线上.(2)、请写出OA , OB , OD三条射线上数字的排列规律.(3)、“2019”在哪条射线上?22. “校园安全”受到全社会的广泛关注,我市某中学对部分学生就校园安全知识的了解程度,采用随机抽样调查的方式,并根据收集到的信息进行统计,绘制了如图两幅尚不完整的统计图,请你根据统计图中所提供的信息解答下列问题:
(1)、“17”在射线上.(2)、请写出OA , OB , OD三条射线上数字的排列规律.(3)、“2019”在哪条射线上?22. “校园安全”受到全社会的广泛关注,我市某中学对部分学生就校园安全知识的了解程度,采用随机抽样调查的方式,并根据收集到的信息进行统计,绘制了如图两幅尚不完整的统计图,请你根据统计图中所提供的信息解答下列问题: (1)、接受问卷调查的学生共有人,扇形统计图中“了解”部分所对应扇形的圆心角为°;(2)、若该中学共有学生900人,请根据上述调查结果,估计该中学学生中对校园安全知识达到“了解”和“基本了解”程度的总人数为人;(3)、若从对校园安全知识达到“了解”程度的3个女生A、B、C和2个男生M、N中分别随机抽取1人参加校园安全知识竞赛,请用树状图或列表法求出恰好抽到女生A的概率.23. 在矩形ABCD中,点E在BC上,AE=AD , DF⊥AE , 垂足为F .
(1)、接受问卷调查的学生共有人,扇形统计图中“了解”部分所对应扇形的圆心角为°;(2)、若该中学共有学生900人,请根据上述调查结果,估计该中学学生中对校园安全知识达到“了解”和“基本了解”程度的总人数为人;(3)、若从对校园安全知识达到“了解”程度的3个女生A、B、C和2个男生M、N中分别随机抽取1人参加校园安全知识竞赛,请用树状图或列表法求出恰好抽到女生A的概率.23. 在矩形ABCD中,点E在BC上,AE=AD , DF⊥AE , 垂足为F . (1)、求证:DF=AB;(2)、若∠FDC=30°,且AB=4,求AD .24. 在一条笔直的公路上依次有A,C,B三地,甲、乙两人同时出发,甲从A地骑自行车去B地,途经C地休息1分钟,继续按原速骑行至B地,甲到达B地后,立即按原路原速返回A地;乙步行从B地前往A地.甲、乙两人距A地的路程y(米)与时间x(分)之间的函数关系如图所示,请结合图象解答下列问题:
(1)、求证:DF=AB;(2)、若∠FDC=30°,且AB=4,求AD .24. 在一条笔直的公路上依次有A,C,B三地,甲、乙两人同时出发,甲从A地骑自行车去B地,途经C地休息1分钟,继续按原速骑行至B地,甲到达B地后,立即按原路原速返回A地;乙步行从B地前往A地.甲、乙两人距A地的路程y(米)与时间x(分)之间的函数关系如图所示,请结合图象解答下列问题: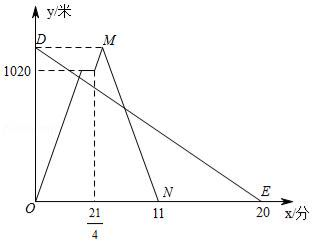 (1)、请写出甲的骑行速度为米/分,点M的坐标为;(2)、求甲返回时距A地的路程y与时间x之间的函数关系式(不需要写出自变量的取值范围);(3)、请直接写出两人出发后,在甲返回A地之前,经过多长时间两人距C地的路程相等.25. 在平面直角坐标系中,抛物线y=x2﹣2x+c(c为常数)的对称轴如图所示,且抛物线过点C(0,c).
(1)、请写出甲的骑行速度为米/分,点M的坐标为;(2)、求甲返回时距A地的路程y与时间x之间的函数关系式(不需要写出自变量的取值范围);(3)、请直接写出两人出发后,在甲返回A地之前,经过多长时间两人距C地的路程相等.25. 在平面直角坐标系中,抛物线y=x2﹣2x+c(c为常数)的对称轴如图所示,且抛物线过点C(0,c). (1)、当c=﹣3时,点(x1 , y1)在抛物线y=x2﹣2x+c上,求y1的最小值;(2)、若抛物线与x轴有两个交点,自左向右分别为点A、B,且OA= OB,求抛物线的解析式;(3)、当﹣1<x<0时,抛物线与x轴有且只有一个公共点,求c的取值范围.26. 如图,在正方形ABCD中,AB=12,以AB为直径作半圆O , 点P从点A出发,沿AD方向以每秒1个单位的速度向点D运动,点Q从点C出发,沿CB方向以每秒3个单位的速度向点B运动,两点同时开始运动,当一点到达终点后,另一点也随之停止运动.设运动时间为t(s).
(1)、当c=﹣3时,点(x1 , y1)在抛物线y=x2﹣2x+c上,求y1的最小值;(2)、若抛物线与x轴有两个交点,自左向右分别为点A、B,且OA= OB,求抛物线的解析式;(3)、当﹣1<x<0时,抛物线与x轴有且只有一个公共点,求c的取值范围.26. 如图,在正方形ABCD中,AB=12,以AB为直径作半圆O , 点P从点A出发,沿AD方向以每秒1个单位的速度向点D运动,点Q从点C出发,沿CB方向以每秒3个单位的速度向点B运动,两点同时开始运动,当一点到达终点后,另一点也随之停止运动.设运动时间为t(s). (1)、发现:设点M为半圆O上任意一点,则DM的最大值为 , 最小值为;(2)、思考:设PQ交半圆O于点F和点G(点F在点G的上方),当PQ∥AB时,求 的长度;(3)、在运动过程中,PQ和半圆O能否相切?若相切,请求出此时t的值,若不能相切,请说明理由;
(1)、发现:设点M为半圆O上任意一点,则DM的最大值为 , 最小值为;(2)、思考:设PQ交半圆O于点F和点G(点F在点G的上方),当PQ∥AB时,求 的长度;(3)、在运动过程中,PQ和半圆O能否相切?若相切,请求出此时t的值,若不能相切,请说明理由;拓展:点N是半圆O上一点,且S扇形BON=6π,当运动t(s)时,PQ与半圆O的交点恰好为点N , 求此时t的值.