河北省石家庄四十二中2019年中考数学二模考试试卷
试卷更新日期：2020-04-21 类型：中考模拟
一、选择题
-
1. 下列运算结果为正整数的是（ ）A、3÷2 B、（﹣3）2 C、0×（﹣2019） D、2﹣32. 中国的“天眼”绝对是我们中国人的骄傲，它可以一眼看穿130亿光年以外，换句话来说就是它可以接收到130亿光年之外的电磁信号，几乎已经可以达到我们人类现在所了解到的宇宙的极限边缘．数据130亿（精确到亿位）正确表示是（ ）A、1.3×1010 B、1.30×1010 C、0.13×1011 D、130×1083. 用三角板作△ABC的边BC上的高，下列三角板的摆放位置正确是（ ）A、
B、
C、
D、
4. 下列各式运算正确是（ ）A、3y3•5y4＝15y12 B、（ab5）2＝ab10 C、（a3）2＝（a2）3 D、（﹣x）4•（﹣x）6＝﹣x105. 图中的内容是某同学完成的作业，嘉琪帮他做了批改，嘉琪批改正确题数是（ ）
A、2个 B、3个 C、4个 D、5个6. 如图，一艘货轮由A地沿北偏东45°方向航行到C地，在C地改变航向航行到B地，此时观测到C地位于B地北偏西63°方向上，则∠C的度数为（ ）
A、99° B、108° C、118° D、128°7. 如图是一块带有圆形空洞和矩形空洞的小木板，则下列物体中最有可能既可以堵住圆形空洞，又可以堵住矩形空洞的是（ ）
A、正方体 B、球 C、圆锥 D、圆柱体8. 如图，用八根长为4cm的铁丝，首尾相接围成一个正八边形（接点不固定）要将它的四边按图中的方式向内等距离移动acm ， 同时去掉另外四根长为4cm的铁丝（虚线部分）得到一个正方形，则a的值为（ ）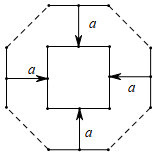
A、4cm B、2cm C、2 cm D、 cm9. 我国古代数学著作《孙子算经》中有一道题：“今有木，不知长短，引绳度之，余绳四尺五，屈绳量之，不足一尺，问木长几何？”大致意思是：“用一根绳子去量一根木条，绳子剩余4.5尺，将绳子对折再量木条，木条剩余1尺，问木条长多少尺？”，设绳子长x尺，木条长y尺，根据题意所列方程组正确是（ ）A、 B、 C、 D、10. 在体育课上，九年级2名学生各练习10次立定跳远，要判断哪一名学生的成绩比较稳定，通常需要比较这2名学生立定跳远成绩的（ ）A、方差 B、平均数 C、频率分布 D、众数11. 已知△ABC ， D是AC上一点，尺规在AB上确定一点E ， 使△ADE∽△ABC ， 则符合要求的作图痕迹是（ ）A、
B、
C、
D、
12. 如图，将Rt△ABC平移到△A'B'C'的位置，其中∠C＝90°使得点C'与△ABC的内心重合，已知AC＝4，BC＝3，则阴影部分的面积为（ ）
A、 B、 C、 D、13. 如图，在矩形ABCD中，E是AD上一点，沿CE折叠△CDE ， 点D恰好落在AC的中点F处，若CD＝ ，则△ACE的面积为（ ）
A、1 B、 C、2 D、214. 如图，在平面直角坐标系中，点A（0，2），点P是双曲线y＝ （x＞0）上的一个动点，做PB⊥x轴于点B ， 当点P的横坐标逐渐减小时，四边形OAPB的面积将会（ ）
A、逐渐增大 B、不变 C、逐渐减小 D、先减小后增大15. 超市有一种“喜之郎“果冻礼盒，内装两个上下倒置的果冻，果冻高为4cm ， 底面是个直径为6cm的圆，轴截面可以近似地看作一个抛物线，为了节省成本，包装应尽可能的小，这个包装盒的长AD（不计重合部分，两个果冻之间没有挤压）至少为（ ）
A、（6+3 ）cm B、（6+2 ）cm C、（6+2 ）cm D、（6+3 ）cm16. 如图，等边△ABC的边长为4，点O是△ABC的外心，∠FOG＝120°．绕点O旋转∠FOG ， 分别交线段AB、BC于D、E两点．连接DE给出下列四个结论：①OD＝OE；②S△ODE＝S△BDE；③S四边形ODBE＝ ；④△BDE周长的最小值为6．上述结论中正确个数是（ ）
A、1 B、2 C、3 D、4二、填空题
-
17. 若m ， n互为相反数，则m2+2mn+n2＝18. 已知直线l1经过点P（1+m ， 1﹣2m），直线l2：y＝kx+k（k≠0），若无论m取何值，直线l1和l2的交点Q都在第一象限，则k的取值范围是19. 如图，正△ABC的边长为2，顶点B、C在半径为 的圆上，顶点A在圆内，将正△ABC绕点B逆时针旋转，当点A第一次落在圆上时，则点C运动的路线长为（结果保留π）；若A点落在圆上记做第1次旋转，将△ABC绕点A逆时针旋转，当点C第一次落在圆上记做第2次旋转，再绕C将△ABC逆时针旋转，当点B第一次落在圆上，记做第3次旋转……，若此旋转下去，当△ABC完成第2017次旋转时，BC边共回到原来位置次．
三、解答题（本大题共7小题，共66分．）
-
20. 老师设计了接力游戏，用合作的方式完成分式化简规则是：每人只能看到前一人给的式子，并进行一步计算，再将结果传递给下一人，最后完成化简过程如图所示：
(1)、接力中，自己负责的一步出现不正确是；(2)、原分式的值能否等于1？如果能，请求出相应的a的值，如果不能，请说明理由．21. 在一节数学活动课上，王老师将本班学生身高数据（精确到1厘米）出示给大家，要求同学们各自独立绘制一幅频数分布直方图，甲绘制的如图①所示，乙绘制的如图②所示，经王老师批改，甲绘制的图是正确，乙在数据整理与绘图过程中均有个别不正确．(1)、写出乙同学在数据整理或绘图过程中的不正确（写出一个即可）；
(2)、甲同学在数据整理后若用扇形统计图表示，则159.5﹣164.5这一部分所对应的扇形圆心角的度数为；(3)、该班学生的身高数据的中位数是；(4)、假设身高在169.5﹣174.5范围的5名同学中，有2名女同学，班主任老师想在这5名同学中选出2名同学作为本班的正、副旗手，那么恰好选中一名男同学和一名女同学当正，副旗手的概率是多少？22. 如图由长为a ， 宽为b的矩形、（2m+1）个长为4，宽为1的小矩形（为正整数）和若干个小圆组成，其中小圆的直径与小矩形的宽相等．
(1)、当m＝1时，a＝ ， b＝；(2)、当a＝24时，求b的值；(3)、a的值能否等于30？请通过计算说明理由；(4)、直接写出a与b的数量关系．23. 如图，在△ABC中，∠B＝∠C＝44°，点D点E分别从点B、点C同时出发，在线段BC上作等速运动，到达C点、B点后运动停止．
(1)、求证：△ABE≌△ACD；(2)、若AB＝BE ， 求∠DAE的度数；(3)、若△ACE的外心在其内部时，求∠BDA的取值范围．24. 某市水费采用阶梯收费制度，即：每月用水不超过15吨时，每吨需缴纳水费a元，每月用水量超过15吨时，超过15吨的部分按每吨提高b元缴纳下表是嘉琪家一至四月份用水量和缴纳水费情况．根据表格提供的数据，回答：月份
一
二
三
四
月用水量（吨）
14
18
16
13
水费（元）
42
60
50
39
(1)、a＝元；b＝元；(2)、求月缴纳水费p（元）与月用水量t（吨）之间的函数关系式；(3)、若嘉琪家五月和六月的月缴水费相差24元，求这两月用水量差的最小值．25. 已知点M（3，2），抛物线L：y＝x2﹣3x+c与x轴从左到右的交点为A ， B ．
(1)、若抛物线L经过点M（3，2），求抛物线L的解析式和顶点坐标；(2)、当2OA＝OB时，求c的值；(3)、直线y＝x+b经过点M ， 与y轴交于点N ，①求点N的坐标；
②若线段MN与抛物线L：y＝x2﹣3x+c有唯一公共点，直接写出正整数c的值．
26. 如图，在矩形ABCD中，AB＝3，BC＝4，半径为1的动圆圆心M从A点出发，沿着AB方向以1个单位长度/每秒的速度匀速运动，同时动点N从点B出发，沿着BD方向也以1个单位长度/每秒的速度匀速运动，设运动的时间为t秒（0≤t≤2.5），以点N为圆心，NB的长为半径的⊙N与BD ， AB的交点分别为E ， F ， 连结EF ， ME ．
(1)、①当t＝秒时，⊙N恰好经过点M；②在运动过程中，当⊙M与△ABD的边相切时，t＝秒；
(2)、当⊙M经过点B时，①求N到AD的距离；②求⊙N被AD截得的弦长；
(3)、若⊙N与线段ME只有一个公共点时，直接写出t的取值范围．