河北省石家庄市新乐市2019年中考数学二模考试试卷

试卷更新日期：2020-04-21 类型：中考模拟

进入出卷网下载

一、选择题

1. 下列各数中，最大的数是（）

A、0 B、﹣ $\frac{2}{3}$ C、0.5 D、2

查看试题解析
2. 如图，已知∠1＝70°，∠2＝110°，∠3＝95°，那么∠4＝（）

A、80° B、85° C、95° D、100°

查看试题解析
3. 下列运算正确是（）

A、2x²•3x＝6x³ B、（2x）³＝6x³ C、x³+x³＝x⁶ D、（2a﹣2b）²＝4a²﹣4b²

查看试题解析
4. 以下四个命题
①两条对角线互相平分的四边形是平行四边形；②两条对角线相等的四边形是矩形；③两条对角线互相垂直的平行四边形是菱形；④有一组邻边相等且有一个角是直角的四边形是正方形，其中是真命题的是（）

A、①② B、③④ C、①③ D、②④

查看试题解析
5. 下列变形不正确是（）

A、 $\frac{x - y}{x^{2} - y^{2}}$ ＝ $\frac{1}{x + y}$ B、 $\frac{1}{x y}$ ÷（ $\frac{1}{x}$ ﹣ $\frac{1}{y}$ ）＝ $\frac{1}{y}$ ﹣ $\frac{1}{x}$ C、 $\frac{- x + y}{2}$ ＝﹣ $\frac{x - y}{2}$ D、 ${(\frac{x^{2}}{- y})}^{3}$ ＝﹣ $\frac{x^{6}}{y^{3}}$

查看试题解析
6. 从图1的正方体上截去一个三棱锥后，得到如图2所示的几何体，则这个几何体的主视图是（）

A、 B、 C、 D、

查看试题解析
7. 如图，纸上画有一个数轴，对折纸面，使数轴上表示﹣3的点与表示4的点重合，那么同时重合的还有（）

A、表示﹣1的点与表示3的点 B、表示﹣2的点与表示2的点 C、表示﹣ $\frac{3}{2}$ 的点与表示 $\frac{2}{3}$ 的点 D、表示﹣ $\frac{5}{2}$ 的点与表示 $\frac{7}{2}$ 的点

查看试题解析
8. 下表列出了某校田径队成员的年龄分布情况：

年龄/岁

13

14

15

16

频数

6

18

n

12﹣n

则对于不同的n ，下列关于年龄的统计量一定不发生改变的是（）

A、众数、中位数 B、中位数、方差 C、平均数、中位数 D、平均数、众数

查看试题解析
9. 菱形OACB在平面直角坐标系中的位置如图所示，点C的坐标是（8，0），点A的纵坐标是2，则点B的坐标是（）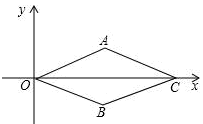

A、（4，2） B、（4，﹣2） C、（2，﹣6） D、（2，6）

查看试题解析
10. 关于x的分式方程 $\frac{2 x - a}{x + 1}$ ＝1的解是不小于﹣3的负数，则下列各数中，a可取的一组数是（）

A、﹣1，1 B、5，6 C、2，3 D、1.5，4

查看试题解析
11. 对于长度为4的线段AB（图1），小若用尺规进行如下操作（图2）根据作图痕迹，有下列说法：①△ABC是等腰三角形；②△ABC是直角三角形；③△ABC是等边三角形；④ $\overset{⌢}{A D}$ 的长度为 $\frac{3}{4} π$ ，⑤△ABC是直角三角形的依据是直径所对的圆周角为直角，则其中正确个数是（）

A、1 B、2 C、3 D、4

查看试题解析
12. 如图，以学校（点C）为观测点，小明家（点B）和小丰家（点A）分别位于学校的正南方向和正西南方向，并测得AC＝6 $\sqrt{2}$ km ， BC＝6（1+ $\sqrt{3}$ ）km ，则小丰家位于小明家的（）

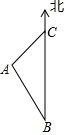A、南偏西30°方向 B、北偏西30°方向 C、北偏东45°方向 D、南偏东60°方向

查看试题解析
13. “今有邑，东西七里，南北九里，各开中门，出东门一十五里有木，问：出南门几何步而见木？”这段话摘自《九章算术》．意思是说：如图，矩形城池ABCD ，东边城墙AB长9里，南边城墙AD长7里，东门点E、南门点F分别是AB、AD中点，EG⊥AB ， FH⊥AD ， EG＝15里，HG经过A点，则FH＝（）

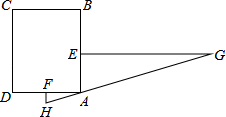A、1.2 里 B、1.5 里 C、1.05 里 D、1.02 里

查看试题解析
14. 矩形Ⅰ的面积为6，矩形Ⅱ中的三条边总长为6，则下列说法不正确是（）

A、矩形Ⅰ中一组邻边的长满足反比例函数关系 B、矩形Ⅰ中一组邻边的长可能是3+ $\sqrt{3}$ 和3﹣ $\sqrt{3}$ C、矩形Ⅰ的周长不可能是8 D、矩形Ⅱ的最大面积是3

查看试题解析
15. 如图1，将正方形ABCD按图1所示置于平面直角坐标系中，AD边与x轴重合，顶点B ， C位于x轴上方，将直线l：y＝x﹣3沿x轴向左以每秒1个单位长度的速度平移，在平移的过程中，该直线被正方形ABCD的边所截得的线段长为m ，平移的时间为t秒，m与t的函数图象如图2所示，则a ， b的值分别是（）

A、6，6 $\sqrt{2}$ B、6，4 $\sqrt{2}$ C、7，7 $\sqrt{2}$ D、7，5 $\sqrt{2}$

查看试题解析

二、填空题

16. 化简： $\sqrt{9}$ + $\sqrt[3]{- 27}$ ＝．

查看试题解析
17. 如图，正五边形和正六边形有一条公共边AB ，并且正五边形在正六边形内部，连接AC并延长，交正六边形于点D ，则∠ADE＝°．

查看试题解析
18. 如图1是一个由1～28的连续整数排成的“数阵”．如图2，用2×2的方框围住了其中的四个数，如果围住的这四个数中的某三个数的和是27，那么这三个数是a ， b ， c ， d中的．

查看试题解析
19. 如图，在扇形AOB中，OA＝OB＝4，∠AOB＝120°，点C是 $\overset{⌢}{A B}$ 上的一个动点（不与点A ， B重合），射线AD与扇形AOB所在⊙O相切，点P在射线AD上，连接AB ， OC ， CP ，若AP＝2 $\sqrt{3}$ ，则CP的取值范围是．

查看试题解析

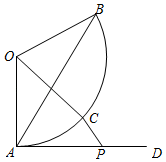
三、解答题

20. 阅读下面的操作规则
第一次操作：对任意相邻的两个数，都用左边的数减去右边的数，所得的差写在这两个数之间，得到一组依次排列的新数串；

第二次操作：对上一次操作得到的新数串，仍按照第一次操作进行，又得到一组依次排列的新数串；

……

这样依次操作下去

(1)、对依次排列的3个数：﹣2，3，6，按上面的规则进行操作，
第一次操作后得到的新数串：﹣2，， 3，， 6此次增加的新数之和为；

(2)、第二次操作后得到的新数申，并求第二次操作后再次增加的新数之和；

(3)、对依次排列的3个数：1，3，﹣ $\frac{1}{2}$ ，按上述规则操作，直接写出第三次操作后再次增加的新数之和是．

查看试题解析
21. 人们利用“公众号”进行学习和获取信息已成为了生活常态，为了解某个学习类公众号的推广情况，小方同学调查统计了从周一到周五对该公众号进行关注的“粉丝”人数的变化情况，并将结果绘制成如图1和图2所示的两个不完整的统计图

根据以上信息，完成下面的问题：

(1)、如图2，周三进行关注的“粉丝”人数对应的扇形圆心角是°；

(2)、将折线统计图补充完整；

(3)、在原来基础上，小方对该公众号又统计了后续周六和周日关注的“粉丝”人数发现这7天平均每天关注的“粉丝”人数比前5天平均每天关注的“粉丝”人数多2人，则
①周六和周日这两天关注了该公众号的一共是人；

②现从周六关注公众号的前3位男士“粉丝”和周日关注公众号的前2位女士“粉丝”中，随机抽取两位进行奖励，请用列表法或者画树状图的方法，求所抽取的两位“粉丝”恰好是一男一女的概率．

查看试题解析
22. 阅读下面的学习材料：
我们知道，一般情况下式子 $\frac{m + n}{3 + 4}$ 与“ $\frac{m}{3} + \frac{n}{4}$ ”是不相等的（m ， n均为整数），但当m ， n取某些特定整数时，可以使这两个式子相等，我们把使“ $\frac{m + n}{3 + 4} = \frac{m}{3} + \frac{n}{4}$ ”成立的数对“m ， n”叫做“好数对”，记作[m ， n]，例如，当m＝n＝0时，有 $\frac{m + n}{3 + 4} = \frac{m}{3} + \frac{n}{4}$ 成立，则数对“0，0”就是一对“好数对”，记作[0，0]

解答下列问题：

(1)、通过计算，判断数对“3，4”是否是“好数对”；

(2)、求“好数对”[x ， ﹣32]中x的值；

(3)、请再写出一对上述未出现的“好数对”[ ， ]；

(4)、对于“好数对[a ， b]，如果a＝9k（k为整数），则b＝（用含k的代数式表示）．

查看试题解析
23. 把两个等腰直角△ABC和△ADE按如图1所示的位置摆放，将△ADE绕点A按逆时针方向旋转，如图2，连接BD ， EC ，设旋转角为α（0°＜α＜360°）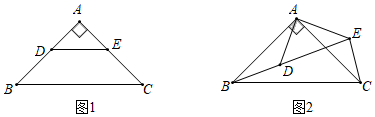

(1)、当DE⊥AC时，AD与BC的位置关系是， AE与BC的位置关系是；

(2)、如图2，当点D在线段BE上时，求∠BEC的度数；

(3)、当旋转角α＝时，△ABD的面积最大．

查看试题解析

24. 某药品生产基地共有5条生产线，每条生产线每月生产药品20万盒，该基地打算从第一个月开始到第五个月结束，对每条生产线进行升级改造．改造时，每个月只升级改造一条生产线，这条生产线当月停产，并于下个月投入生产，其他生产线则正常生产．经调查，每条生产线升级改造后，每月的产量会比原来提高20%．

(1)、根据题意，完成下面问题：

①把下表补充完整（直接写在横线上）：

月数	第1个月	第2个月	第3个月	第4个月	第5个月	第6个月	…
产量/万盒				92	…	…	…

②从第1个月进行升级改造后，第个月的产量开始超过未升级改造时的产量；

(2)、若该基地第x个月（1≤x≤5，且x是整数）的产量为y万盒，求y关于x的函数关系式；

(3)、已知每条生产线的升级改造费是30万元，每盒药品可获利3元．设从第1个月开始升级改造后，生产药品所获总利润为W₁万元；同时期内，不升级改造所获总利润为W₂万元设至少到第n个月（n为正整数）时，W₁大于W₂ ，求n的值．（利润＝获利﹣改造费）

查看试题解析

25. 如图所示，在四边形ABCD中，AD∥BC ， CD⊥BC ， ∠ABC＝60°，且AD＝12，BC＝18．动点P从点A出发，以每秒2个单位长度的速度向点D运动，设运动时间为t秒（0＜t≤6）

(1)、当t＝6时，cos∠BPC＝；

(2)、当△BPC的外接圆与AD相切时，求t的值；

(3)、在点P运动过程中，cos∠BPC是否存在最小值？若存在，请求出这个最小值；若不存在，请说明理由．

查看试题解析
26. 如图，点P为抛物线L：y＝a（x﹣2）（x﹣4）（其中a为常数，且a＜0）的顶点，L与y轴交于点C ，过点C作x轴的平行线，与L交于点A ，过点A作x轴的垂线，与射线OP交于点B ，连接OA

(1)、a＝﹣2时，点P的坐标是，点B的坐标是；

(2)、是否存在a的值，使OA＝OB？若存在，求出a的值；若不存在，请说明理由

(3)、若△OAB的外心N的坐标为（p ， q），则
①当点N在△OAB内部时，求a的取值范围；

②用a表示外心N的横坐标p和纵坐标q ，并求p与q的关系式（不写q的取值范围）．

查看试题解析

年龄/岁	13	14	15	16
频数	6	18	n	12﹣n