河北省石家庄市桥西区2019年中考数学二模考试试卷
试卷更新日期:2020-04-21 类型:中考模拟
一、选择题
-
1. 计算: 得( )A、 B、 C、 D、2. 将数据162000用科学记数法表示为( )A、0.162×105 B、1.62×105 C、16.2×104 D、162×1033. 如图,数轴上点A、B、C、D表示的数中,表示互为相反数的两个点是( )
 A、点B和点C B、点A和点C C、点B和点D D、点A和点D4.
A、点B和点C B、点A和点C C、点B和点D D、点A和点D4.中国讲究五谷丰登,六畜兴旺,如图是一个正方体展开图,图中的六个正方形内分别标有六畜:“猪”、“牛”、“羊”、“马”、“鸡”、“狗”.将其围成一个正方体后,则与“牛”相对的是( )
 A、羊 B、马 C、鸡 D、狗5. 有理数a、b在数轴上的位置如图,则下列结论正确是( )
A、羊 B、马 C、鸡 D、狗5. 有理数a、b在数轴上的位置如图,则下列结论正确是( ) A、﹣a<﹣b<a<b B、a<﹣b<b<﹣a C、﹣b<a<﹣a<b D、a<b<﹣b<﹣a6. 如图,在Rt△ABC中,∠ACB=90°,以BC为直径作圆,交斜边AB于点E , D为AC的中点.连接DO , DE . 则下列结论中不一定正确是( )
A、﹣a<﹣b<a<b B、a<﹣b<b<﹣a C、﹣b<a<﹣a<b D、a<b<﹣b<﹣a6. 如图,在Rt△ABC中,∠ACB=90°,以BC为直径作圆,交斜边AB于点E , D为AC的中点.连接DO , DE . 则下列结论中不一定正确是( ) A、DO∥AB B、△ADE是等腰三角形 C、DE⊥AC D、DE是⊙O的切线7. 下列计算,正确是( )A、( )﹣1=2 B、| |=﹣ C、 D、8. 已知四边形ABCD中,对角线AC与BD相交于点O , AD∥BC , 下列判断中不正确是( )A、如果AB=CD , AC=BD , 那么四边形ABCD是矩形 B、如果AB∥CD , AC=BD , 那么四边形ABCD是矩形 C、如果AD=BC , AC⊥BD , 那么四边形ABCD是菱形 D、如果OA=OC , AC⊥BD , 那么四边形ABCD是菱形9. 若式子 +(k﹣1)0有意义,则一次函数y=(k﹣1)x+1﹣k的图象可能是( )A、
A、DO∥AB B、△ADE是等腰三角形 C、DE⊥AC D、DE是⊙O的切线7. 下列计算,正确是( )A、( )﹣1=2 B、| |=﹣ C、 D、8. 已知四边形ABCD中,对角线AC与BD相交于点O , AD∥BC , 下列判断中不正确是( )A、如果AB=CD , AC=BD , 那么四边形ABCD是矩形 B、如果AB∥CD , AC=BD , 那么四边形ABCD是矩形 C、如果AD=BC , AC⊥BD , 那么四边形ABCD是菱形 D、如果OA=OC , AC⊥BD , 那么四边形ABCD是菱形9. 若式子 +(k﹣1)0有意义,则一次函数y=(k﹣1)x+1﹣k的图象可能是( )A、 B、
B、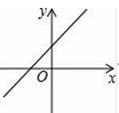 C、
C、 D、
D、 10. 如果从甲船看乙船,乙船在甲船的南偏东30°方向,那么从乙船看甲船,甲船在乙船的( )A、北偏东30° B、北偏西30° C、北偏东60° D、北偏西60°11. 下列判断正确是( )A、高铁站对旅客的行李的检查应采取抽样调查 B、一组数据5、3、4、5、3的众数是5 C、“掷一枚硬币正面朝上的概率是 ”表示每抛掷硬币2次就必有1次反面朝上 D、甲,乙组数据的平均数相同,方差分别是S甲2=4.3,S乙2=4.1,则乙组数据更稳定12. 已知2是关于x的方程x2﹣(5+m)x+5m=0的一个根,并且这个方程的两个根恰好是等腰△ABC的两条边长,则△ABC的周长为( )A、9 B、12 C、9或12 D、6或12或1513. 如图,在△ABC中,∠C=90°,BC=6,点D,E分别在AB,AC上,将△ABC沿DE折叠,使点A落在点A′处,若CA′= AA',则折痕DE的长为( )
10. 如果从甲船看乙船,乙船在甲船的南偏东30°方向,那么从乙船看甲船,甲船在乙船的( )A、北偏东30° B、北偏西30° C、北偏东60° D、北偏西60°11. 下列判断正确是( )A、高铁站对旅客的行李的检查应采取抽样调查 B、一组数据5、3、4、5、3的众数是5 C、“掷一枚硬币正面朝上的概率是 ”表示每抛掷硬币2次就必有1次反面朝上 D、甲,乙组数据的平均数相同,方差分别是S甲2=4.3,S乙2=4.1,则乙组数据更稳定12. 已知2是关于x的方程x2﹣(5+m)x+5m=0的一个根,并且这个方程的两个根恰好是等腰△ABC的两条边长,则△ABC的周长为( )A、9 B、12 C、9或12 D、6或12或1513. 如图,在△ABC中,∠C=90°,BC=6,点D,E分别在AB,AC上,将△ABC沿DE折叠,使点A落在点A′处,若CA′= AA',则折痕DE的长为( ) A、4 B、3 C、2 D、14. 某校举行“社会主义核心价值观”演讲比赛,学校对30名参赛选手的成绩进行了分组统计,结果如下表:
A、4 B、3 C、2 D、14. 某校举行“社会主义核心价值观”演讲比赛,学校对30名参赛选手的成绩进行了分组统计,结果如下表:分数x(分)
4≤x<5
5≤x<6
6≤x<7
7≤x<8
8≤x<9
9≤x<10
频数
2
6
8
5
5
4
由上可知,参赛选手分数的中位数所在的分数段为( )
A、5≤x<6 B、6≤x<7 C、7≤x<8 D、8≤x<915. 已知点A(﹣2,y1),B(a , y2),C(3,y3)都在反比例函数y= 的图象上,且﹣2<a<0,则( )A、y1<y2<y3 B、y3<y2<y1 C、y3<y1<y2 D、y2<y1<y316. 已知正方形MNOK和正六边形ABCDEF边长均为1,把正方形放在正六边形中,使OK边与AB边重合,如图所示:按下列步骤操作:将正方形在正六边形中绕点B顺时针旋转,使KM边与BC边重合,完成第一次旋转;再绕点C顺时针旋转,使MN边与CD边重合,完成第二次旋转……连续经过六次旋转.在旋转的过程中,当正方形和正六边形的边重合时,点B,M间的距离可能是( ) A、0.5 B、0.7 C、 ﹣1 D、 ﹣1
A、0.5 B、0.7 C、 ﹣1 D、 ﹣1二、填空题
-
17. 已知x=y+95,则代数式x2﹣2xy+y2﹣25= .18. 如图,已知点E , F分别是▱ABCD的边BC , AD上的中点,且∠BAC=90°,若∠B=30°,BC=10,则四边形AECF的面积为 .
 19. 在平面直角坐标系xOy中,已知直线l:y=x , 作A1(1,0)关于y=x的对称点B1 , 将点B1向右水平平移2个单位得到点A2;再作A2关于y=x的对称点B2 , 将点B2向右水平平移2个单位得到点A3;….请继续操作并探究:点A3的坐标是 , 点B2014的坐标是 .
19. 在平面直角坐标系xOy中,已知直线l:y=x , 作A1(1,0)关于y=x的对称点B1 , 将点B1向右水平平移2个单位得到点A2;再作A2关于y=x的对称点B2 , 将点B2向右水平平移2个单位得到点A3;….请继续操作并探究:点A3的坐标是 , 点B2014的坐标是 .三、解答题
-
20. 分解因式:(x+1)(x﹣4)+3x .21. 计算: .22. 为了开展阳光体育运动,坚持让中小学生“每天锻炼一小时”,体育局做了一个随机调查,调查内容是:每天锻炼是否超过1h及锻炼未超过1h的原因.他们随机调查了340名学生,用所得的数据制成了扇形统计图和频数分布直方图(图1、图2).

根据图示,请回答以下问题:
(1)、“没时间”的人数是 , 并补全频数分布直方图;(2)、2015年全市中小学生约18万人,按此调查,可以估计2015年全市中小学生每天锻炼超过1h的约有万人;(3)、在(2)的条件下,如果计划2017年全市中小学生每天锻炼未超过1h的人数减少到8.64万人,求2015年至2017年锻炼未超过1h人数的年平均降低的百分率.23. 如图,在矩形ABCD中,点F在边BC上,且AF=AD , 过点D作DE⊥AF , 垂足为点E (1)、求证:DE=AB;(2)、以A为圆心,AB长为半径作圆弧交AF于点G , 若BF=FC=1,求扇形ABG的面积.(结果保留π)24. 如图,四边形ABCD的四个顶点分别在反比例函数y= 与y= (x>0,0<m<n)的图象上,对角线BD∥y轴,且BD⊥AC于点P . 已知点B的横坐标为4.
(1)、求证:DE=AB;(2)、以A为圆心,AB长为半径作圆弧交AF于点G , 若BF=FC=1,求扇形ABG的面积.(结果保留π)24. 如图,四边形ABCD的四个顶点分别在反比例函数y= 与y= (x>0,0<m<n)的图象上,对角线BD∥y轴,且BD⊥AC于点P . 已知点B的横坐标为4.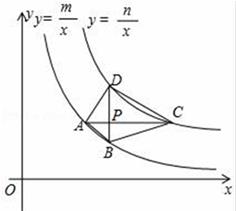 (1)、当m=4,n=20时.
(1)、当m=4,n=20时.①若点P的纵坐标为2,求直线AB的函数表达式.
②若点P是BD的中点,试判断四边形ABCD的形状,并说明理由.
(2)、四边形ABCD能否成为正方形?若能,求此时m , n之间的数量关系;若不能,试说明理由.25. 如图,是一副学生用的三角板,在△ABC 中,∠C=90°,∠A=60°,∠B=30°;在△A1B1C1中,∠C1=90°,∠A1=45°,∠B1=45°,且A1B1=CB . 若将边A1C1与边CA重合,其中点A1与点C重合.将三角板A1B1C1绕点C(A1)按逆时针方向旋转,旋转过的角为α,旋转过程中边A1C1与边AB的交点为M , 设AC=a .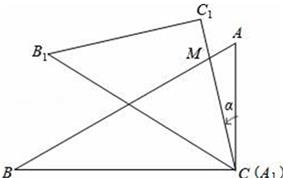 (1)、计算A1C1的长;(2)、当α=30°时,证明:B1C1∥AB;(3)、若a= ,当α=45°时,计算两个三角板重叠部分图形的面积;(4)、当α=60°时,用含a的代数式表示两个三角板重叠部分图形的面积.
(1)、计算A1C1的长;(2)、当α=30°时,证明:B1C1∥AB;(3)、若a= ,当α=45°时,计算两个三角板重叠部分图形的面积;(4)、当α=60°时,用含a的代数式表示两个三角板重叠部分图形的面积.(参考数据:sin15°= ,cos15°= ,tan15°=2﹣ ,sin75°= ,cos75°= ,tan75°=2+ )
26. 已知,抛物线y=ax2+ax+b(a≠0)与直线y=2x+m有一个公共点M(1,0),且a<b.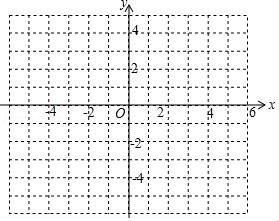 (1)、求b与a的关系式和抛物线的顶点D坐标(用a的代数式表示);(2)、直线与抛物线的另外一个交点记为N,求△DMN的面积与a的关系式;(3)、a=﹣1时,直线y=﹣2x与抛物线在第二象限交于点G,点G、H关于原点对称,现将线段GH沿y轴向上平移t个单位(t>0),若线段GH与抛物线有两个不同的公共点,试求t的取值范围.
(1)、求b与a的关系式和抛物线的顶点D坐标(用a的代数式表示);(2)、直线与抛物线的另外一个交点记为N,求△DMN的面积与a的关系式;(3)、a=﹣1时,直线y=﹣2x与抛物线在第二象限交于点G,点G、H关于原点对称,现将线段GH沿y轴向上平移t个单位(t>0),若线段GH与抛物线有两个不同的公共点,试求t的取值范围.