2015年安徽省中考数学真题试卷

试卷更新日期：2016-04-21 类型：中考真卷

进入出卷网下载

一、单选题

1. 在﹣4，2，﹣1，3这四个数中，比﹣2小的数是（　　）

A、-4 B、2 C、-1 D、3

查看试题解析
2. 计算 $\sqrt{8}$ × $\sqrt{2}$ 的结果是（　　）

A、 $\sqrt{10}$ B、4 C、 $\sqrt{6}$ D、2

查看试题解析
3. 移动互联网已经全面进入人们的日常生活．截止2015年3月，全国4G用户总数达到1.62亿，其中1.62亿用科学记数法表示为（　　）

A、1.62× $10^{4}$ B、1.62× $10^{6}$ C、1.62× $10^{8}$ D、0.162× $10^{9}$

查看试题解析
4. 下列几何体中，俯视图是矩形的是（　　）

A、 B、 C、 D、

查看试题解析
5. 与1+ $\sqrt{5}$ 最接近的整数是（　　）

A、4 B、3 C、2 D、1

查看试题解析
6. 我省2013年的快递业务量为1.4亿件，受益于电子商务发展和法治环境改善等多重因素，快递业务迅猛发展，2014年增速位居全国第一．若2015年的快递业务量达到4.5亿件，设2014年与2013年这两年的平均增长率为x，则下列方程正确的是（　　）

A、1.4（1+x）=4.5 B、1.4（1+2x）=4.5 C、1.4 $(1 + x)^{2}$ =4.5 D、1.4（1+x）+1.4 $(1 + x)^{2}$ =4.5

查看试题解析
7. 某校九年级（1）班全体学生2015年初中毕业体育考试的成绩统计如下表：
成绩（分）
35
39
42
44
45
48
50
人数（人）
2
5
6
6
8
7
6
根据上表中的信息判断，下列结论中错误的是（　　）

A、该班一共有40名同学 B、该班学生这次考试成绩的众数是45分 C、该班学生这次考试成绩的中位数是45分 D、该班学生这次考试成绩的平均数是45分

查看试题解析
8. 在四边形ABCD中，∠A=∠B=∠C，点E在边AB上，∠AED=60°，则一定有（　　）

A、∠ADE=20° B、∠ADE=30° C、∠ADE= $\frac{1}{2}$ ∠ADC D、∠ADE= $\frac{1}{3}$ ∠ADC

查看试题解析
9.
如图，矩形ABCD中，AB=8，BC=4．点E在边AB上，点F在边CD上，点G、H在对角线AC上．若四边形EGFH是菱形，则AE的长是
（　　）

A、 $2 \sqrt{5}$ B、 $3 \sqrt{5}$ C、5 D、6

查看试题解析
10.
如图，一次函数y₁=x与二次函数y₂=ax²+bx+c图象相交于P、Q两点，则函数y=ax²+（b﹣1）x+c的图象可能是（　　）

A、 B、 C、 D、

查看试题解析

二、填空题

11. ﹣64的立方根是．

查看试题解析
12.
如图，点A、B、C在半径为9的⊙O上，的长为2π，则∠ACB的大小是．

查看试题解析
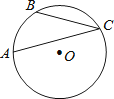13. 按一定规律排列的一列数：2¹ ， 2² ， 2³ ， 2⁵ ， 2⁸ ， 2¹³ ， …，若x、y、z表示这列数中的连续三个数，猜想x、y、z满足的关系式是．

查看试题解析
14. 已知实数a、b、c满足a+b=ab=c，有下列结论：
①若c≠0，则 $\frac{1}{a}$ + $\frac{1}{b}$ =1； ②若a=3，则b+c=9； ③若a=b=c，则abc=0； ④若a、b、c中只有两个数相等，则a+b+c=8．
其中正确的是　　（把所有正确结论的序号都选上）．

查看试题解析

三、计算题

15. 先化简，再求值：（ $\frac{a^{2}}{a - 1}$ + $\frac{1}{1 - a}$ ）• $\frac{1}{a}$ ，其中a= $- \frac{1}{2}$ ．

查看试题解析
16. 解不等式： $\frac{x}{3}$ ＞1﹣ $\frac{x - 3}{6}$ ．

查看试题解析

四、解答题

17.
如图，在边长为1个单位长度的小正方形网格中，给出了△ABC（顶点是网格线的交点）．
（1）请画出△ABC关于直线l对称的△A₁B₁C₁；
（2）将线段AC向左平移3个单位，再向下平移5个单位，画出平移得到的线段A₂C₂ ，并以它为一边作一个格点△A₂B₂C₂ ，使A₂B₂=C₂B₂ ．

查看试题解析
18.
如图，平台AB高为12m，在B处测得楼房CD顶部点D的仰角为45°，底部点C的俯角为30°，求楼房CD的高度（ $\sqrt{3}$ =1.7）．

查看试题解析

五、综合题

19. A、B、C三人玩篮球传球游戏，游戏规则是：第一次传球由A将球随机地传给B、C两人中的某一人，以后的每一次传球都是由上次的传球者随机地传给其他两人中的某一人．

(1)、求两次传球后，球恰在B手中的概率；

(2)、求三次传球后，球恰在A手中的概率．

查看试题解析
20.
在⊙O中，直径AB=6，BC是弦，∠ABC=30°，点P在BC上，点Q在⊙O上，且OP⊥PQ．

(1)、如图1，当PQ∥AB时，求PQ的长度；

(2)、如图2，当点P在BC上移动时，求PQ长的最大值．

查看试题解析
21.
如图，已知反比例函数y= $\frac{k_{1}}{x}$ 与一次函数y=k₂x+b的图象交于点A（1，8）、B（﹣4，m）．

(1)、求k₁、k₂、b的值；

(2)、求△AOB的面积；

(3)、若M（x₁ ， y₁）、N（x₂ ， y₂）是反比例函数y= $\frac{k_{1}}{x}$ 图象上的两点，且x₁＜x₂ ， y₁＜y₂ ，指出点M、N各位于哪个象限，并简要说明理由．

查看试题解析
22.
如图1，在四边形ABCD中，点E、F分别是AB、CD的中点，过点E作AB的垂线，过点F作CD的垂线，两垂线交于点G，连接AG、BG、CG、DG，且∠AGD=∠BGC．

(1)、求证：AD=BC；

(2)、求证：△AGD∽△EGF；

(3)、如图2 ，若AD、BC所在直线互相垂直，求 $\frac{A D}{E F}$ 的值．

查看试题解析
23.
为了节省材料，某水产养殖户利用水库的岸堤（岸堤足够长）为一边，用总长为80m的围网在水库中围成了如图所示的①②③三块矩形区域，而且这三块矩形区域的面积相等．设BC的长度为xm，矩形区域ABCD的面积为ym² ．

(1)、求y与x之间的函数关系式，并注明自变量x的取值范围；

(2)、x为何值时，y有最大值？最大值是多少？

查看试题解析

成绩（分）	35	39	42	44	45	48	50
人数（人）	2	5	6	6	8	7	6