河北省廊坊市广阳区2019年中考数学一模考试试卷
试卷更新日期:2020-04-21 类型:中考模拟
一、选择题
-
1. 已知图中所有的小正方形都全等,若在右图中再添加一个全等的小正方形得到新的图形,使新图形是中心对称图形,则正确添加方案是( )
 A、
A、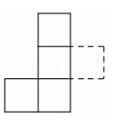 B、
B、 C、
C、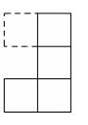 D、
D、 2. 估算+÷的运算结果应在( )A、1到2之间 B、2到3之间 C、3到4之间 D、4到5之间3. 港珠澳大桥是世界最长的跨海大桥整个大桥造价超过720亿元人民币,720亿用科学记数法可表示为( )元.A、7.2×1010 B、0.72×1011 C、7.2×1011 D、7.2×1094. 为了增强学生体质,学校发起评选“健步达人”活动,小明用计步器记录自己一个月(30天)每天走的步数,并绘制成如下统计表:
2. 估算+÷的运算结果应在( )A、1到2之间 B、2到3之间 C、3到4之间 D、4到5之间3. 港珠澳大桥是世界最长的跨海大桥整个大桥造价超过720亿元人民币,720亿用科学记数法可表示为( )元.A、7.2×1010 B、0.72×1011 C、7.2×1011 D、7.2×1094. 为了增强学生体质,学校发起评选“健步达人”活动,小明用计步器记录自己一个月(30天)每天走的步数,并绘制成如下统计表:步数(万步)
1.0
1.2
1.1
1.4
1.3
天数
3
3
5
7
12
在每天所走的步数这组数据中,众数和中位数分别是( )
A、1.3,1.1 B、1.3,1.3 C、1.4,1.4 D、1.3,1.45. 在联欢会上,甲、乙、丙3人分别站在不在同一直线上的三点A、B、C上,他们在玩抢凳子的游戏,要在他们中间放一个木凳,谁先抢到凳子谁获胜,为使游戏公平,凳子应放的最恰当的位置是△ABC的( )A、三条高的交点 B、重心 C、内心 D、外心6. 在△ABC中,点D是边BC上的点(与B , C两点不重合),过点D作DE∥AC , DF∥AB , 分别交AB , AC于E , F两点,下列说法正确是( ) A、若AD⊥BC , 则四边形AEDF是矩形 B、若AD垂直平分BC , 则四边形AEDF是矩形 C、若BD=CD , 则四边形AEDF是菱形 D、若AD平分∠BAC , 则四边形AEDF是菱形7. 如图所示,小兰用尺规作图作△ABC边AC上的高BH , 作法如下:
A、若AD⊥BC , 则四边形AEDF是矩形 B、若AD垂直平分BC , 则四边形AEDF是矩形 C、若BD=CD , 则四边形AEDF是菱形 D、若AD平分∠BAC , 则四边形AEDF是菱形7. 如图所示,小兰用尺规作图作△ABC边AC上的高BH , 作法如下:①分别以点DE为圆心,大于DE的长为半径作弧两弧交于F;②作射线BF , 交边AC于点H;③以B为圆心,BK长为半径作弧,交直线AC于点D和E;④取一点K使K和B在AC的两侧;所以BH就是所求作的高.其中顺序正确作图步骤是( )
 A、①②③④ B、④③①② C、②④③① D、④③②①8. 下列命题为假命题的是( )A、若a=b , 则a﹣2019=b﹣2019 B、若a=b , 则 C、若a>b , 则 a2>ab D、若a<b , 则a﹣2c<b﹣2c9. 如图,已知一渔船上的渔民在A处看见灯塔M在北偏东60°方向,这艘渔船以28海里/时的速度向正东方向航行,半小时后到达B处,在B处看见灯塔M在北偏东15°方向,此时灯塔M与渔船的距离是( )
A、①②③④ B、④③①② C、②④③① D、④③②①8. 下列命题为假命题的是( )A、若a=b , 则a﹣2019=b﹣2019 B、若a=b , 则 C、若a>b , 则 a2>ab D、若a<b , 则a﹣2c<b﹣2c9. 如图,已知一渔船上的渔民在A处看见灯塔M在北偏东60°方向,这艘渔船以28海里/时的速度向正东方向航行,半小时后到达B处,在B处看见灯塔M在北偏东15°方向,此时灯塔M与渔船的距离是( ) A、7 海里 B、14 海里 C、7海里 D、14海里10. 如果a﹣3b=0,那么代数式(a﹣ )÷ 的值是( )A、 B、- C、 D、111. 关于x的不等式组 有三个整数解,则a的取值范围是( )A、 B、 C、 D、12. 将若干个大小相等的正五边形排成环状,如图所示是前3个五边形,要完成这一圆环还需( )个正五边形
A、7 海里 B、14 海里 C、7海里 D、14海里10. 如果a﹣3b=0,那么代数式(a﹣ )÷ 的值是( )A、 B、- C、 D、111. 关于x的不等式组 有三个整数解,则a的取值范围是( )A、 B、 C、 D、12. 将若干个大小相等的正五边形排成环状,如图所示是前3个五边形,要完成这一圆环还需( )个正五边形 A、6 B、7 C、8 D、913. 如图,以AD为直径的半圆O经过Rt△ABC斜边AB的两个端点,交直角边AC于点E;B、E是半圆弧的三等分点, 的长为 ,则图中阴影部分的面积为( )
A、6 B、7 C、8 D、913. 如图,以AD为直径的半圆O经过Rt△ABC斜边AB的两个端点,交直角边AC于点E;B、E是半圆弧的三等分点, 的长为 ,则图中阴影部分的面积为( ) A、 B、 C、 D、14. 若正整数按如图所示的规律排列则第十一行第五列的数字是( )
A、 B、 C、 D、14. 若正整数按如图所示的规律排列则第十一行第五列的数字是( ) A、121 B、113 C、115 D、11715. 如图,已知边长为4的正方形ABCD , E是BC边上一动点(与B、C不重合),连结AE , 作EF⊥AE交∠BCD的外角平分线于F , 设BE=x , △ECF的面积为y , 下列图象中,能表示y与x的函数关系的图象大致是( )
A、121 B、113 C、115 D、11715. 如图,已知边长为4的正方形ABCD , E是BC边上一动点(与B、C不重合),连结AE , 作EF⊥AE交∠BCD的外角平分线于F , 设BE=x , △ECF的面积为y , 下列图象中,能表示y与x的函数关系的图象大致是( ) A、
A、 B、
B、 C、
C、 D、
D、 16. 如图,已知△ABC中,AB=AC , ∠BAC=90°,直角∠EPF的顶点P是BC中点,两边PE , PF分别交AB , AC于点E , F , 当∠EPF在△ABC内绕顶点P旋转时(点E不与A , B重合),给出以下五个结论:①AE=CF;②∠APE=∠CPF;③连接EF , △EPF是等腰直角三角形;④EF=AP;⑤S四边形AFPE=S△APC , 其中正确有几个( )
16. 如图,已知△ABC中,AB=AC , ∠BAC=90°,直角∠EPF的顶点P是BC中点,两边PE , PF分别交AB , AC于点E , F , 当∠EPF在△ABC内绕顶点P旋转时(点E不与A , B重合),给出以下五个结论:①AE=CF;②∠APE=∠CPF;③连接EF , △EPF是等腰直角三角形;④EF=AP;⑤S四边形AFPE=S△APC , 其中正确有几个( )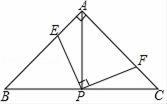 A、2个 B、3个 C、4个 D、5个
A、2个 B、3个 C、4个 D、5个二、填空題
-
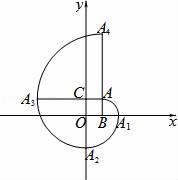
17. 已知a>0,那么 =.18. 分解因式: = .19. 如图,在平面直角坐标系中,四边形ABOC是正方形,点A的坐标为(1,1),弧 是以点B为圆心,BA为半径的圆弧; 是以点O为圆心,OA1为半径的圆弧; 是以点C为圆心,CA2为半径的圆弧; 是以点A为圆心,AA3为半径的圆弧,继续以点B , O , C , A为圆心按上述作法得到的曲线AA1A2A3A4A5…称为正方形的“渐开线”,则点 A4的坐标是 , 那么 A4n+1的坐标为 .
三、解答题
-
20. 观察下列等式:2× =2+ ,3× =3+ ,4× =4+ ,…(1)、按此规律写出第5个等式;(2)、猜想第n个等式,并说明等式成立的理由.21. 如图,△BAD是由△BEC在平面内绕点B逆时针旋转60°而得,且AB⊥BC , BE=CE , 连接DE .
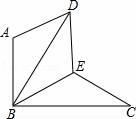 (1)、求证:△BDE≌△BCE;(2)、试判断四边形ABED的形状.并说明理由.22. 主题班会上,王老师出示了如图所示的一幅漫画,经过同学们的一番热议,达成以下四个观点:
(1)、求证:△BDE≌△BCE;(2)、试判断四边形ABED的形状.并说明理由.22. 主题班会上,王老师出示了如图所示的一幅漫画,经过同学们的一番热议,达成以下四个观点:A.放下自我,彼此尊重; B.放下利益,彼此平衡;
C.放下性格,彼此成就; D.合理竞争,合作双赢.
要求每人选取其中一个观点写出自己的感悟.根据同学们的选择情况,小明绘制了下面两幅不完整的图表,请根据图表中提供的信息,解答下列问题:
观点
频数
频率
A
a
0.2
B
12
0.24
C
8
b
D
20
0.4
 (1)、参加本次讨论的学生共有人;表中a= , b=;(2)、在扇形统计图中,求D所在扇形的圆心角的度数;(3)、现准备从A,B,C,D四个观点中任选两个作为演讲主题,请用列表或画树状图的方法求选中观点D(合理竞争,合作双赢)的概率.23. 如图,在平面直角坐标系xOy中,一次函数y=kx+b(k≠0)的图象与反比例函数y= (n≠0)的图象交于第二、四象限内的A、B两点与x轴交于点C , 点B坐标为(m , ﹣1),AD⊥x轴,且AD=3,tan∠AOD=
(1)、参加本次讨论的学生共有人;表中a= , b=;(2)、在扇形统计图中,求D所在扇形的圆心角的度数;(3)、现准备从A,B,C,D四个观点中任选两个作为演讲主题,请用列表或画树状图的方法求选中观点D(合理竞争,合作双赢)的概率.23. 如图,在平面直角坐标系xOy中,一次函数y=kx+b(k≠0)的图象与反比例函数y= (n≠0)的图象交于第二、四象限内的A、B两点与x轴交于点C , 点B坐标为(m , ﹣1),AD⊥x轴,且AD=3,tan∠AOD= (1)、求该反比例函数和一次函数的解析式;(2)、连接OB , 求S△AOC﹣S△BOC的值;(3)、点E是x轴上一点,且△AOE是等腰三角形请直接写出满足条件的E点的个数(写出个数即可,不必求出E点坐标).24. 例1:在等腰三角形ABC , ∠A=120°,求B的度数.
(1)、求该反比例函数和一次函数的解析式;(2)、连接OB , 求S△AOC﹣S△BOC的值;(3)、点E是x轴上一点,且△AOE是等腰三角形请直接写出满足条件的E点的个数(写出个数即可,不必求出E点坐标).24. 例1:在等腰三角形ABC , ∠A=120°,求B的度数.例2:在等腰三角形ABC中,∠A=50°,求∠B的度数.
王老师启发同学们进行变式,小兰编了如下一题:变式等腰三角形ABC中,∠A=70°,求∠B的度数;
 (1)、请你解答小兰的变式题;(2)、解完(1)后,小兰发现,∠A的度数不同,得到∠B的度数的个数也可能不同,如果在等腰三角形ABC中,设∠A=x°;
(1)、请你解答小兰的变式题;(2)、解完(1)后,小兰发现,∠A的度数不同,得到∠B的度数的个数也可能不同,如果在等腰三角形ABC中,设∠A=x°;①当∠B的度数唯一时请你探索x的取值范围并用含x的式子表示∠B的度数;
②当∠B有三个不同的度数时请你探索x的取值范围,并用含x的式子表示∠B的度数.
25. 某种蔬菜的售单价y1与销售月份x之间的关系如图1所示,成本y2与销售月份x之间的关系如图2所示(图1的图象是线段,图2的图象是抛物线)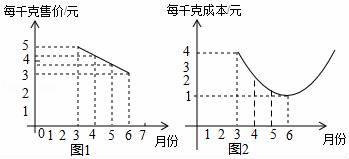 (1)、已知6月份这种蔬菜的成本最低,此时出售每千克的利润是多少元?(利润=售价﹣成本);(2)、设每千克该蔬菜销售利润为P , 请列出x与P之间的函数关系式,并求出哪个月出售这种蔬菜每千克的利润最大,最大利润是多少?(3)、已知市场部销售该种蔬菜4、5个月的总利润为22万元,且5月份的销售量比4月份的销售量多2万千克.求4、5两个月的销售量分别是多少万千克?26. 如图①.抛物线y=ax2+bx+3(a≠0)与x轴、y轴分别交于A(﹣1,0)、B(3,0)、C三点.
(1)、已知6月份这种蔬菜的成本最低,此时出售每千克的利润是多少元?(利润=售价﹣成本);(2)、设每千克该蔬菜销售利润为P , 请列出x与P之间的函数关系式,并求出哪个月出售这种蔬菜每千克的利润最大,最大利润是多少?(3)、已知市场部销售该种蔬菜4、5个月的总利润为22万元,且5月份的销售量比4月份的销售量多2万千克.求4、5两个月的销售量分别是多少万千克?26. 如图①.抛物线y=ax2+bx+3(a≠0)与x轴、y轴分别交于A(﹣1,0)、B(3,0)、C三点. (1)、求a和b的值;(2)、点D(2,m)在第一象限的抛物线上,连接BC、BD、CD , 在对称轴左侧的抛物线上存在一点P , 满足∠PBC=∠DBC , 请求出点P的坐标;(3)、如图②,在(2)的条件下将△BOC沿x轴正方向以每秒1个单位长度的速度向右平移,记平移后的三角形为△B'O'C'在平移过程中,△B'O'C'与△BCD重叠部分的面积记为S , 设平移的时间为t秒,请直接写出S与t之间的函数关系式(并注明自变量的取值范围).
(1)、求a和b的值;(2)、点D(2,m)在第一象限的抛物线上,连接BC、BD、CD , 在对称轴左侧的抛物线上存在一点P , 满足∠PBC=∠DBC , 请求出点P的坐标;(3)、如图②,在(2)的条件下将△BOC沿x轴正方向以每秒1个单位长度的速度向右平移,记平移后的三角形为△B'O'C'在平移过程中,△B'O'C'与△BCD重叠部分的面积记为S , 设平移的时间为t秒,请直接写出S与t之间的函数关系式(并注明自变量的取值范围).