河北省廊坊市安次区2019年中考数学二模考试试卷
试卷更新日期:2020-04-21 类型:中考模拟
一、选择题
-
1. 下列四个运算中,结果最小的是( )A、﹣1+(﹣2) B、1﹣(﹣2) C、1×(﹣2) D、1÷(﹣2)2. 下列各图是一些常用图形的标志,其中是轴对称图形但不是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 下列计算结果为a2的是( )A、a8÷a4(a≠0) B、a2•a C、﹣3a2+(﹣2a)2 D、a4﹣a24. 下列命题中,①13个人中至少有2人的生日是同一个月是必然事件;②一名篮球运动员投篮命中概率为0.7,他投篮10次,一定会命中7次;③因为任何数的平方都是正数,所以任何数的平方根都是正数;④在平面上任意画一个三角形,其内角和一定是180°,正确个数是( )A、1 B、2 C、3 D、45. 如图是由7个同样大小的正方体摆成的几何体.将正方体①移走后,所得几何体( )
3. 下列计算结果为a2的是( )A、a8÷a4(a≠0) B、a2•a C、﹣3a2+(﹣2a)2 D、a4﹣a24. 下列命题中,①13个人中至少有2人的生日是同一个月是必然事件;②一名篮球运动员投篮命中概率为0.7,他投篮10次,一定会命中7次;③因为任何数的平方都是正数,所以任何数的平方根都是正数;④在平面上任意画一个三角形,其内角和一定是180°,正确个数是( )A、1 B、2 C、3 D、45. 如图是由7个同样大小的正方体摆成的几何体.将正方体①移走后,所得几何体( )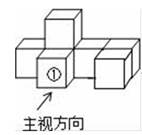 A、主视图改变,俯视图改变 B、左视图改变,俯视图改变 C、俯视图不变,左视图改变 D、主视图不变,左视图不变6. 关于 的叙述正确是( )A、在数轴上不存在表示 的点 B、 = + C、 =±2 D、与 最接近的整数是37. 定义新运算:a※b= ,则函数y=3※x的图象大致是( )A、
A、主视图改变,俯视图改变 B、左视图改变,俯视图改变 C、俯视图不变,左视图改变 D、主视图不变,左视图不变6. 关于 的叙述正确是( )A、在数轴上不存在表示 的点 B、 = + C、 =±2 D、与 最接近的整数是37. 定义新运算:a※b= ,则函数y=3※x的图象大致是( )A、 B、
B、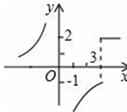 C、
C、 D、
D、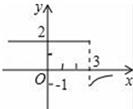 8. 关于二次函数y=2x2+4x﹣1,下列说法正确是( )A、图象与y轴的交点坐标为(0,1) B、图象的对称轴在y轴的右侧 C、当x<0时,y的值随x值的增大而减小 D、y的最小值为﹣39. 如图,△ABC的面积为12,AC=3,现将△ABC沿AB所在直线翻折,使点C落在直线AD上的C处,P为直线AD上的一点,则线段BP的长可能是( )
8. 关于二次函数y=2x2+4x﹣1,下列说法正确是( )A、图象与y轴的交点坐标为(0,1) B、图象的对称轴在y轴的右侧 C、当x<0时,y的值随x值的增大而减小 D、y的最小值为﹣39. 如图,△ABC的面积为12,AC=3,现将△ABC沿AB所在直线翻折,使点C落在直线AD上的C处,P为直线AD上的一点,则线段BP的长可能是( )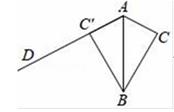 A、3 B、5 C、6 D、1010. 为了帮助我市一名贫困学生,某校组织捐款,现从全校所有学生的捐款数额中随机抽取10名学生的捐款数统计如下表:
A、3 B、5 C、6 D、1010. 为了帮助我市一名贫困学生,某校组织捐款,现从全校所有学生的捐款数额中随机抽取10名学生的捐款数统计如下表:捐款金额/元
20
30
50
90
人数
2
4
3
1
则下列说法正确是( )
A、10名学生是总体的一个样本 B、中位数是40 C、众数是90 D、方差是40011. 下列图案中花边的内外边缘(每个图形边缘等宽)所围成的图形不相似的是( )A、 B、
B、 C、
C、 D、
D、 12. 把边长相等的正六边形ABCDEF和正五边形GHCDL的CD边重合,按照如图所示的方式叠放在一起,延长LG交AF于点P , 则∠APG=( )
12. 把边长相等的正六边形ABCDEF和正五边形GHCDL的CD边重合,按照如图所示的方式叠放在一起,延长LG交AF于点P , 则∠APG=( )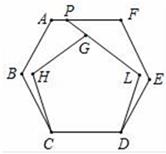 A、141° B、144° C、147° D、150°13. 如图,在已知的△ABC中,按以下步骤作图:①分别以B、C为圆心,以大于 BC的长为半径作弧,两弧相交于点M、N;②作直线MN交AB于点D , 连接CD , 若CD=AD , ∠B=20°,则下列结论中不正确是( )
A、141° B、144° C、147° D、150°13. 如图,在已知的△ABC中,按以下步骤作图:①分别以B、C为圆心,以大于 BC的长为半径作弧,两弧相交于点M、N;②作直线MN交AB于点D , 连接CD , 若CD=AD , ∠B=20°,则下列结论中不正确是( )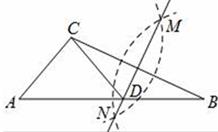 A、∠CAD=40° B、∠ACD=70° C、点D为△ABC的外心 D、∠ACB=90°14. 如图,点A是量角器直径的一个端点,点B在半圆周上,点P在 上,点Q在AB上,且PB=PQ . 若点P对应140°(40°),则∠PQB的度数为( )
A、∠CAD=40° B、∠ACD=70° C、点D为△ABC的外心 D、∠ACB=90°14. 如图,点A是量角器直径的一个端点,点B在半圆周上,点P在 上,点Q在AB上,且PB=PQ . 若点P对应140°(40°),则∠PQB的度数为( )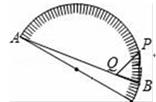 A、65° B、70° C、75° D、80°15. 如图,在平面直角坐标系xOy中,菱形ABCD的顶点A的坐标为(2,0),点B的坐标为(0,1),对角线BD与x轴平行,若直线y=kx+5+2k(k≠0)与菱形ABCD有交点,则k的取值范围是( )
A、65° B、70° C、75° D、80°15. 如图,在平面直角坐标系xOy中,菱形ABCD的顶点A的坐标为(2,0),点B的坐标为(0,1),对角线BD与x轴平行,若直线y=kx+5+2k(k≠0)与菱形ABCD有交点,则k的取值范围是( )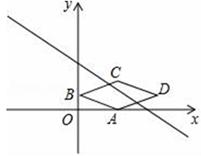 A、 B、 C、 D、﹣2≤k≤2且k≠016. 将正整数1至2018按一定规律排列如下表:
A、 B、 C、 D、﹣2≤k≤2且k≠016. 将正整数1至2018按一定规律排列如下表: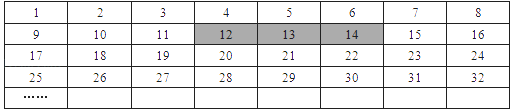
平移表中带阴影的方框,方框中三个数的和可能是( )
A、2019 B、2018 C、2016 D、2013二、填空题
-
17. 当a,b互为相反数,则代数式a2+ab﹣2的值为 .
18. 如图,在平面直角坐标系中,点A的坐标为(2.5,1),连接OA并延长至点B , 使OA=AB , 则点B的坐标是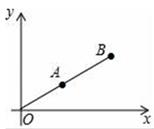 19. 如图,在等边△ABC内有一点D , AD=5,BD=6,CD=4,将△ABD绕A点逆时针旋转,使AB与AC重合,点D旋转至点E .
19. 如图,在等边△ABC内有一点D , AD=5,BD=6,CD=4,将△ABD绕A点逆时针旋转,使AB与AC重合,点D旋转至点E .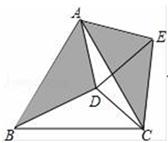 (1)、DE=;(2)、∠CDE的正切值为 .
(1)、DE=;(2)、∠CDE的正切值为 .三、简答題
-
20.(1)、计算:(﹣ )﹣2﹣ +6cos30°;(2)、先化简,再求值:(a+b)(a﹣b)﹣(a﹣2b)2 , 其中a=2,b=﹣1.21. 如图,自左向右,水平摆放一组小球,按照以下规律排列,如:红球,黄球,绿球,红球,黄球,绿球,…,嘉琪依次在小球上标上数字1,2,3,4,5,6,…
尝试:左数第三个黄球上标的数字是多少?
应用:若某个小球上标的数字是101,则这个小球的颜色是什么?它左边共有多少个与它颜色相同的小球?
发现:试用含n的代数式表示左边第n个黄球所标的数字.
 22. 今年5月13日是“母亲节”,某校开展“感恩母亲,做点家务”活动为了了解同学们在母亲节这一天做家务情况,学校随机抽查了部分同学,并用得到的数据制成如下不完整的统计表:
22. 今年5月13日是“母亲节”,某校开展“感恩母亲,做点家务”活动为了了解同学们在母亲节这一天做家务情况,学校随机抽查了部分同学,并用得到的数据制成如下不完整的统计表:做家务时间(小时)
人数
所占百分比
A组:0.5
15
30%
B组:1
30
60%
C组:1.5
x
4%
D组:2
3
6%
合计
y
100%
(1)、统计表中的x= , y=;(2)、小君计算被抽查同学做家务时间的平均数是这样的:第一步:计算平均数的公式是 ,
第二步:该问题中n=4,x1=0.5,x2=1,x3=1.5,x4=2,
第三步: =1.25(小时)
(3)、现从C , D两组中任选2人,求这2人都在D组中的概率(用树形图法或列表法).23. 如图,已知A、F、C、D四点在同一条直线上,AF=CD , AB∥DE , 且AB=DE .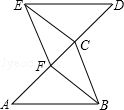 (1)、求证:△ABC≌△DEF;(2)、若EF=3,DE=4,∠DEF=90°,请直接写出使四边形EFBC为菱形时AF的长度.24. 如图,在平面直角坐标系xOy中,一次函数y=ax﹣a(a为常数)的图象与y轴相交于点A , 与函数y= (x>0)的图象相交于点B(t , 1).
(1)、求证:△ABC≌△DEF;(2)、若EF=3,DE=4,∠DEF=90°,请直接写出使四边形EFBC为菱形时AF的长度.24. 如图,在平面直角坐标系xOy中,一次函数y=ax﹣a(a为常数)的图象与y轴相交于点A , 与函数y= (x>0)的图象相交于点B(t , 1).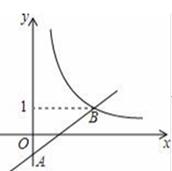 (1)、求点B的坐标及一次函数的解析式;(2)、点P的坐标为(m , m)(m>0),过P作PE∥x轴,交直线AB于点E , 作PF∥y轴,交函数y= (x>0)的图象于点F .
(1)、求点B的坐标及一次函数的解析式;(2)、点P的坐标为(m , m)(m>0),过P作PE∥x轴,交直线AB于点E , 作PF∥y轴,交函数y= (x>0)的图象于点F .①若m=2,比较线段PE , PF的大小;
②直接写出使PE≤PF的m的取值范围.
25. 抛物线L:y=a(x﹣x1)(x﹣x2)(常数a≠0)与x轴交于点A(x1 , 0),B(x2 , 0),与y轴交于点C , 且x1•x2<0,AB=4,当直线l:y=﹣3x+t+2(常数t>0)同时经过点A , C时,t=1.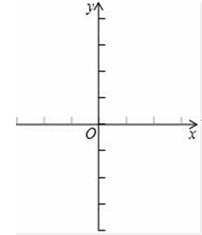 (1)、点C的坐标是;(2)、求点A , B的坐标及L的顶点坐标;(3)、在如图2 所示的平面直角坐标系中,画出L的大致图象;(4)、将L向右平移t个单位长度,平移后y随x的增大而增大部分的图象记为G , 若直线l与G有公共点,直接写出t的取值范围.26. 如图,在矩形ABCD中,AB=6,BC=8,O是AD的中点,以O为圆心在AD的下方作半径为3的半圆O , 交AD于E、F .
(1)、点C的坐标是;(2)、求点A , B的坐标及L的顶点坐标;(3)、在如图2 所示的平面直角坐标系中,画出L的大致图象;(4)、将L向右平移t个单位长度,平移后y随x的增大而增大部分的图象记为G , 若直线l与G有公共点,直接写出t的取值范围.26. 如图,在矩形ABCD中,AB=6,BC=8,O是AD的中点,以O为圆心在AD的下方作半径为3的半圆O , 交AD于E、F .思考:连接BD , 交半圆O于G、H , 求GH的长;
探究:将线段AF连带半圆O绕点A顺时针旋转,得到半圆O′,设其直径为E'F′,旋转角为α(0<α<180°).
 (1)、设F′到AD的距离为m , 当m> 时,求α的取值范围;(2)、若半圆O′与线段AB、BC相切时,设切点为R , 求 的长.
(1)、设F′到AD的距离为m , 当m> 时,求α的取值范围;(2)、若半圆O′与线段AB、BC相切时,设切点为R , 求 的长.(sin49°= ,cos41°= ,tan37°= ,结果保留π)