河北省保定市莲池区2019年中考数学一模考试试卷

试卷更新日期：2020-04-21 类型：中考模拟

进入出卷网下载

一、选择题

1. 下列各组数中数值不相等的是（）

A、﹣2³和（﹣2）³ B、2^﹣1和 $- \frac{1}{2}$ C、2⁰和1 D、|2|和﹣（﹣2）

查看试题解析
2. 用激光测距仪测量两座山峰之间的距离，从一座山峰发出的激光经过4×10^﹣5秒到达另一座山峰，已知光在空气中的速度约为3×10⁸米/秒，则这两座山峰之间的距离用科学记数法表示为（）

A、1.2×10³米 B、12×10³米 C、1.2×10⁴米 D、1.2×10⁵米

查看试题解析
3. 如图是小明画的正方体表面展开图，由7个相同的正方形组成．小颖认为小明画的不对，她剪去其中的一个正方形后，得到的平面图就可以折成一个正方体．小颖剪去的正方形的编号是（）

A、7 B、6 C、5 D、4

查看试题解析
4. 以O为中心点的量角器与直角三角板ABC如图所示摆放，直角顶点B在零刻度线所在直线DE上，且量角器与三角板只有一个公共点P ，若点P的读数为35°，则∠CBD的度数是（）

A、55° B、45° C、35° D、25

查看试题解析
5. 已知关于x的不等式组 ${\begin{matrix} x - a > 0 \\ 2 - 2 x > 0 \end{matrix}$ 的整数解共有6个，则a的取值范围是（）

A、﹣6＜a＜﹣5 B、﹣6≤a＜﹣5 C、﹣6＜a≤﹣5 D、﹣6≤a≤﹣5

查看试题解析
6. 在中考复习中，老师出了一道题“化简 $\frac{x + 3}{x + 2} + \frac{2 - x}{x^{2} - 4}$ ”．下列是甲、乙、丙三位同学的做法，下列判断正确是（）
甲：原式＝ $\frac{(x + 3) (x - 2)}{x^{2} - 4} - \frac{x - 2}{x^{2} - 4} = \frac{(x + 3) (x - 2) - x - 2}{x^{2} - 4} = \frac{x^{2} - 8}{x^{2} - 4}$ ；

乙：原式＝（x+3）（x﹣2）+（2﹣x）＝x²+x﹣6+2﹣x＝x²﹣4

丙：原式＝ $\frac{x + 3}{x + 2} - \frac{x - 2}{(x + 2) (x - 2)} = \frac{x + 3}{x + 2} - \frac{1}{x + 2} = \frac{x + 3 - 1}{x + 2}$ ＝1

A、甲正确 B、乙正确 C、丙正确 D、三人均错误

查看试题解析
7. 若关于x的一元二次方程ax²+2x﹣5＝0的两根中有且仅有一根在0和1之间（不含0和1），则a的取值范围是（）

A、a＜3 B、a＞3 C、a＜﹣3 D、a＞﹣3

查看试题解析
8. 如果（a+b）²﹣（a﹣b）²=4，则一定成立的是（）

A、a是b的相反数 B、a是﹣b的相反数 C、a是b的倒数 D、a是﹣b的倒数

查看试题解析
9. 函数y＝ $\sqrt{3 x + 6}$ 中自变量x的取值范围在数轴上表示正确是（）

A、 B、 C、 D、

查看试题解析

10. 甲、乙两名同学分别进行6次射击训练，训练成绩（单位：环）如下表

	第一次	第二次	第三次	第四次	第五次	第六次
甲	9	8	6	7	8	10
乙	8	7	9	7	8	8

对他们的训练成绩作如下分析，其中说法正确是（）

A、他们训练成绩的平均数相同 B、他们训练成绩的中位数不同 C、他们训练成绩的众数不同 D、他们训练成绩的方差不同

查看试题解析

11. 将一副三角尺（在Rt△ABC中，∠ACB＝90°，∠B＝60°，在Rt△EDF中，∠EDF＝90°，∠E＝45°）如图摆放，点D为AB的中点，DE交AC于点P ， DF经过点C ，将△EDF绕点D顺时针方向旋转α（0°＜α＜60°），DE′交AC于点M ， DF′交BC于点N ，则 $\frac{P M}{C N}$ 的值为（）

A、 $\sqrt{3}$ B、 $\frac{\sqrt{3}}{2}$ C、 $\frac{\sqrt{3}}{3}$ D、 $\frac{1}{2}$

查看试题解析
12. 某服装厂准备加工400套运动装，在加工完160套后，采用了新技术，使得工作效率比原计划提高了20%，结果共用了18天完成任务，问计划每天加工服装多少套？在这个问题中，设计划每天加工x套服装，则根据题意可得方程为（）

A、 $\frac{160}{x}$ + $\frac{400 - 160}{(1 + 20 %) x}$ =18 B、 $\frac{160}{x}$ + $\frac{400}{(1 + 20 %) x}$ =18 C、 $\frac{160}{x}$ + $\frac{400 - 160}{20 % x}$ =18 D、 $\frac{400}{x}$ + $\frac{400 - 160}{(1 + 20 %) x}$ =18

查看试题解析
13. 为了测量被池塘隔开的A ， B两点之间的距离，根据实际情况，作出如图所示的图形，其中AB⊥BE ， EF⊥BE ， AF交BE于点D ， C在BD上，有四位同学分别测量出以下四组数据：①BC ， ∠ACB；②CD ， ∠ACB ， ∠ADB；③EF ， DE ， BD；④DE ， DC ， BC ．能根据所测数据，求出A、B间距离的有（）

A、4组 B、3组 C、2组 D、1组

查看试题解析
14. 一个长为2、宽为1的长方形以下面的四种“姿态”从直线l的左侧水平平移至右侧（下图中的虚线都是水平线）.其中，所需平移的距离最短的是（）

A、 B、 C、 D、

查看试题解析
15. 甲、乙、丙三位同学进行立定跳远比赛，每人轮流跳一次称为一轮，每轮按名次从高到低分别得3分、2分、1分（没有并列名次）．他们一共进行了五轮比赛，结果甲共得14分；乙第一轮得3分，第二轮得1分，且总分最低，那么丙得到的分数是（）

A、8分 B、9分 C、10分 D、11分

查看试题解析
16. 如图，已知抛物线y＝x²+bx+c与直线y＝x交于（1，1）和（3，3）两点，现有以下结论：①b²﹣4c＞0；②3b+c+6＝0；③当x²+bx+c＞ $\frac{2}{x}$ 时，x＞2；④当1＜x＜3时，x²+（b﹣1）x+c＜0，其中正确序号是（）

A、①②④ B、②③④ C、②④ D、③④

查看试题解析

二、填空题

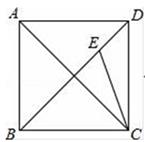
17. 若x、y为实数，且|x+3|+ $\sqrt{y - 3}$ =0，则 $（ \frac{x}{y} ）^{2019}$ 的值为．

查看试题解析
18. 如图，已知正方形ABCD的边长为1，连接AC、BD ， CE平分∠ACD交BD于点E ，则DE＝．

查看试题解析
19. 如图，O是边长为1的等边△ABC的中心，将AB、BC、CA分别绕点A、点B、点C顺时针旋转α（0°＜α＜180°），得到AB′、BC′、CA′，连接A′B′、B′C′、A′C′、OA′、OB′．

(1)、∠A′OB′＝°；

(2)、当α＝°时，△A′B′C′的周长最大．

查看试题解析

三、解答题

20. 如图，在一条不完整的数轴上从左到右有点A ， B ．将线段AB沿数轴向右移动，移动后的线段记为A′B′，按要求完成下列各小题

(1)、若点A为数轴原点，点B表示的数是4，当点A′恰好是AB的中点时，数轴上点B′表示的数为．

(2)、设点A表示的数为m ，点A′表示的数为n ，当原点在线段A′B之间时，化简回|m|+|n|+|m﹣n|．

查看试题解析
21. 我们生活在一个充满轴对称的世界中，从自然景观到分子结构，从建筑物到艺术作品，甚至日常生活用品，都可以找到轴对称的影子
我们把形如aa ， bcb ， bccb ， abcba的正整数叫“轴对称数”，例如：33，151，2442，.56765，…

(1)、写出一个最小的四位“轴对称数”：．

(2)、设任意一个n（n≥3）位的“轴对称数”为ABA ，其中首位和末位数字为A ，去掉首尾数字后的（n﹣2）位数表示为B ，求证：该“轴对称数”与它个位数字的11倍的差能被10整除．为了让同学们更好的解答本题，王老师给出了一些提示，如图所示
33﹣3×11＝3×10+3﹣3×11＝0

151﹣1×11＝1×100+5×10+1﹣1×11＝140

2442﹣2×11＝2×1000+44×10+2﹣2×11＝2420

①请根据上面的提示，填空：56765﹣5×11═ ．

查看试题解析
22. 为有效利用电力资源，某市电力局采用“峰谷”用电政策，每天8：00﹣22：00为“峰时段”，22：00至次日8：00为“谷时段”．嘉淇家使用的是峰谷电价，他将家里2018年1月至5月的峰时段和谷时段用电量绘制成如图所示的条形统计图，已知嘉淇家1月份电费为51.8元，2月份电费为50.85元．

(1)、“峰电”每度元，“谷电”每度；

(2)、嘉淇家3月份用电量比这5个月的平均用电量少1度，且3月份所交电费为49.54元，则3月份“峰电”度数为度；

(3)、2018年6月，嘉淇单位决定给职工补贴前五个月中的两个月份的电费，求恰好选中3月份和4月份的概率．

查看试题解析
23. 如图，在△ABC中，AD为边BC上的中线，且AD平分∠BAC ．嘉淇同学先是以A为圆心，任意长为半径画弧，交AD于点P ，交AC于点Q ，然后以点C为圆心，AP长为半径画弧，交AC于点M ，再以M为圆心，PQ长为半径画弧，交前弧于点N ，作射线CN ，交BA的延长线于点E ．

(1)、通过嘉淇的作图方法判断AD与CE的位置关系是，数量关系是；

(2)、求证：AB＝AC；

(3)、若BC＝24，CE＝10，求△ABC的内心到BC的距离．

查看试题解析
24. 甲、乙两人相约周末沿同一条路线登山，甲、乙两人距地面的高度y（米）与登山时间x（分钟）之间的函数图象如图所示，根据图象所提供的信息解答下列问题

(1)、甲登山的速度是每分钟米；乙在A地提速时，甲距地面的高度为米；

(2)、若乙提速后，乙的速度是甲登山速度的3倍；
①求乙登山全过程中，登山时距地面的高度y（米）与登山时间x（分钟）之间的函数解析式；

②乙计划在他提速后5分钟内追上甲，请判断乙的计划能实现吗？并说明理由；

(3)、当x为多少时，甲、乙两人距地面的高度差为80米？

查看试题解析
25. 已知P（﹣3，m）和 Q（1，m）是抛物线y＝x²+bx﹣3上的两点．

(1)、求b的值；

(2)、将抛物线y＝x²+bx﹣3的图象向上平移k（是正整数）个单位，使平移后的图象与x轴无交点，求k的最小值；

(3)、将抛物线y＝x²+bx﹣3的图象在x轴下方的部分沿x轴翻折，图象的其余部分保持不变，得到一个新的图象，请你结合新图象回答：当直线y＝x+n与这个新图象有两个公共点时，求n的取值范围．

查看试题解析
26. 问题提出

(1)、如图①，在△ABC中，∠A＝120°，AB＝AC＝5，则△ABC的外接圆半径R的值为．
问题探究

(2)、如图②，⊙O的半径为13，弦AB＝24，M是AB的中点，P是⊙O上一动点，求PM的最大值．
问题解决

(3)、如图③所示，AB、AC、 $\overset{⌢}{B C}$ 是某新区的三条规划路，其中AB＝6km ， AC＝3km ， ∠BAC＝60°， $\overset{⌢}{B C}$ 所对的圆心角为60°，新区管委会想在 $\overset{⌢}{B C}$ 路边建物资总站点P ，在AB ， AC路边分别建物资分站点E、F ，也就是，分别在 $\overset{⌢}{B C}$ 、线段AB和AC上选取点P、E、F ．由于总站工作人员每天都要将物资在各物资站点间按P→E→F→P的路径进行运输，因此，要在各物资站点之间规划道路PE、EF和FP ．为了快捷、环保和节约成本．要使得线段PE、EF、FP之和最短，试求PE+EF+FP的最小值．（各物资站点与所在道路之间的距离、路宽均忽略不计）

查看试题解析