河北省保定市定兴县固城镇二中2019年中考数学二模考试试卷
试卷更新日期:2020-04-21 类型:中考模拟
一、选择题
-
1. 下列图形中,线段MN的长度表示点M到直线l的距离的是( )A、
 B、
B、 C、
C、 D、
D、 2. 关于“线段、角、正方形、平行四边形、圆”这些图形中,其中是轴对称图形的个数为( )A、2 B、3 C、4 D、53. 下列运算中,正确是( )A、(x2)3=x5 B、x2+2x3=3x5 C、(﹣ab)3=a3b D、x3•x3=x64. 数学课上,老师在黑板上写了四个式子,如图所示,其中计算结果为整数的是( )
2. 关于“线段、角、正方形、平行四边形、圆”这些图形中,其中是轴对称图形的个数为( )A、2 B、3 C、4 D、53. 下列运算中,正确是( )A、(x2)3=x5 B、x2+2x3=3x5 C、(﹣ab)3=a3b D、x3•x3=x64. 数学课上,老师在黑板上写了四个式子,如图所示,其中计算结果为整数的是( )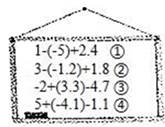 A、① B、② C、③ D、④5. 如图是由几个相同的正方体搭成的一个几何体,从正面看到的平面图形是( )
A、① B、② C、③ D、④5. 如图是由几个相同的正方体搭成的一个几何体,从正面看到的平面图形是( )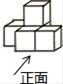 A、
A、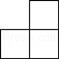 B、
B、 C、
C、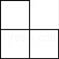 D、
D、 6. 根据制定中的通州区总体规划,将通过控制人口总量上限的方式,努力让副中心远离“城市病”.预计到2035年,副中心的常住人口规模将控制在130万人以内,初步建成国际一流的和谐宜居现代化城区.130万用科学记数法表示为( )A、 B、 C、 D、7. 如图,Rt△ABC中,∠C=90°,∠A<∠B , 且∠A≠30°,以△ABC的一边为边画等腰三角形,使得它的第三个顶点P在△ABC的其他边上,则可以画出不同的点P的个数为( )
6. 根据制定中的通州区总体规划,将通过控制人口总量上限的方式,努力让副中心远离“城市病”.预计到2035年,副中心的常住人口规模将控制在130万人以内,初步建成国际一流的和谐宜居现代化城区.130万用科学记数法表示为( )A、 B、 C、 D、7. 如图,Rt△ABC中,∠C=90°,∠A<∠B , 且∠A≠30°,以△ABC的一边为边画等腰三角形,使得它的第三个顶点P在△ABC的其他边上,则可以画出不同的点P的个数为( )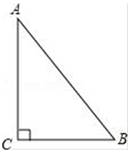 A、4 B、5 C、6 D、78. 下面是嘉嘉和琪琪的对话,根据对话内容,则x的值可能是
A、4 B、5 C、6 D、78. 下面是嘉嘉和琪琪的对话,根据对话内容,则x的值可能是嘉嘉:我能正确化简分式( )÷
琪琪:我给x取一个值,使你化简分式后所得代数式的值大于0,你能猜出来我给x取的值是几吗?( )
A、﹣1 B、1 C、0 D、29. 若一个正六边形的边心距为2 ,则该正六边形的周长为( )A、24 B、24 C、12 D、410. 七年级1班甲、乙两个小组的14名同学身高(单位:厘米)如下:甲组
158
159
160
160
160
161
169
乙组
158
159
160
161
161
163
165
以下叙述不正确是( )
A、甲组同学身高的众数是160 B、乙组同学身高的中位数是161 C、甲组同学身高的平均数是161 D、两组相比,乙组同学身高的方差大11. 如图,边长为4的等边△ABC中,D、E分别为AB , AC的中点,则△ADE的面积是( ) A、 B、 C、 5 D、212.
A、 B、 C、 5 D、212.如图,要修建一条公路,从A村沿北偏东75°方向到B村,从B村沿北偏西25°方向到C村.若要保持公路CE与AB的方向一致,则∠ECB的度数为( )
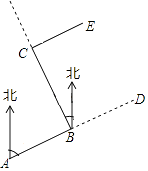 A、80° B、90° C、100° D、105°13. 如图,将△ABC沿BC边上的中线AD平移到△A'B'C'的位置,已知△ABC的面积为9,阴影部分三角形的面积为4.若AA'=1,则A'D等于( )
A、80° B、90° C、100° D、105°13. 如图,将△ABC沿BC边上的中线AD平移到△A'B'C'的位置,已知△ABC的面积为9,阴影部分三角形的面积为4.若AA'=1,则A'D等于( )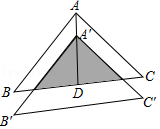 A、2 B、3 C、 D、14. 如图,小明为了测量河宽AB , 先在BA延长线上取一点D , 再在同岸取一点C , 测得∠CAD=60°,∠BCA=30°,AC=15m , 那么河AB宽为( )
A、2 B、3 C、 D、14. 如图,小明为了测量河宽AB , 先在BA延长线上取一点D , 再在同岸取一点C , 测得∠CAD=60°,∠BCA=30°,AC=15m , 那么河AB宽为( )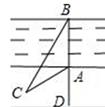 A、15m B、 m C、 m D、 m15. 边长为2的正方形内接于⊙O , 则⊙O的半径是( )A、1 B、 C、2 D、216. 二次函数y=x2+bx﹣1的图象如图,对称轴为直线x=1,若关于x的一元二次方程x2﹣2x﹣1﹣t=0(t为实数)在﹣1<x<4的范围内有实数解,则t的取值范围是( )
A、15m B、 m C、 m D、 m15. 边长为2的正方形内接于⊙O , 则⊙O的半径是( )A、1 B、 C、2 D、216. 二次函数y=x2+bx﹣1的图象如图,对称轴为直线x=1,若关于x的一元二次方程x2﹣2x﹣1﹣t=0(t为实数)在﹣1<x<4的范围内有实数解,则t的取值范围是( )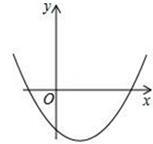 A、t≥﹣2 B、﹣2≤t<7 C、﹣2≤t<2 D、2<t<7
A、t≥﹣2 B、﹣2≤t<7 C、﹣2≤t<2 D、2<t<7二、填空题
-
17. 化简 = .18. 已知a、b互为相反数,c、d互为倒数,代数式3a+3b﹣4cd的值是 .19. 如图,在△ABC中,BC=AC=5,AB=8,CD为AB边的高,点A在x轴上,点B在y轴上,点C在第一象限,若A从原点出发,沿x轴向右以每秒1个单位长的速度运动,则点B随之沿y轴下滑,并带动△ABC在平面内滑动,设运动时间为t秒,当B到达原点时停止运动
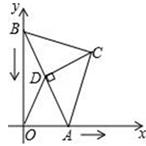 (1)、连接OC , 线段OC的长随t的变化而变化,当OC最大时,t=;(2)、当△ABC的边与坐标轴平行时,t= .
(1)、连接OC , 线段OC的长随t的变化而变化,当OC最大时,t=;(2)、当△ABC的边与坐标轴平行时,t= .三、解答题
-
20. 暑假里某班同学相约一起去某公园划船,在售票处了解到该公园划船项目收费标准如下:
船型
两人船(仅限两人)
四人船(仅限四人)
六人船(仅限六人)
八人船(仅限八人)
每船租金(元/小时)

100
130
 (1)、其中,两人船项目和八人船项目单价模糊不清,通过询问,了解到以下信息:
(1)、其中,两人船项目和八人船项目单价模糊不清,通过询问,了解到以下信息:①一只八人船每小时的租金比一只两人船每小时的租金的2倍少30元;
②租2只两人船,3只八人船,游玩一个小时,共需花费630元.
请根据以上信息,求出两人船项目和八人船项目每小时的租金;
(2)、若该班本次共有18名同学一起来游玩,每人乘船的时间均为1小时,且每只船均坐满,试列举出可行的方案(至少四种),通过观察和比较,找到所有方案中最省钱的方案.21. 6月14日是“世界献血日”,某市采取自愿报名的方式组织市民义务献血.献血时要对献血者的血型进行检测,检测结果有“A型”、“B型”、“AB型”、“O型”4种类型.在献血者人群中,随机抽取了部分献血者的血型结果进行统计,并根据这个统计结果制作了两幅不完整的图表: (1)、这次随机抽取的献血者人数为人,m=;(2)、补全上表中的数据;
(1)、这次随机抽取的献血者人数为人,m=;(2)、补全上表中的数据;血型
A
B
AB
O
人数
10
5
(3)、若这次活动中该市有3000人义务献血,请你根据抽样结果回答:从献血者人群中任抽取一人,其血型是A型的概率是多少?并估计这3000人中大约有多少人是A型血?
22. 如图,在Rt△ABC中∠C=90°,BC=7cm . 动点P在线段AC上从点C出发,沿CA方向运动;动点Q在线段BC上同时从点B出发,沿BC方向运动.如果点P , Q的运动速度均为lcm/s , 那么运动几秒时,它们相距5cm . 23. 如图,O为▱ABCD对角线交点,过O的两直线m、n互相垂直,且与四边形各边相交于E、F、G、H . 试判断四边形EFGH的形状,并给出证明.
23. 如图,O为▱ABCD对角线交点,过O的两直线m、n互相垂直,且与四边形各边相交于E、F、G、H . 试判断四边形EFGH的形状,并给出证明. 24. 如图,在平面直角坐标系中,反比例函数y= (x>0)的图象与边长是6的正方形OABC的两边AB , BC分别相交于M , N两点.
24. 如图,在平面直角坐标系中,反比例函数y= (x>0)的图象与边长是6的正方形OABC的两边AB , BC分别相交于M , N两点.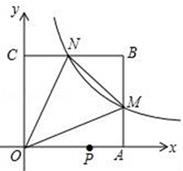 (1)、若点M是AB边的中点,求反比例函数y= 的解析式和点N的坐标;(2)、若AM=2,求直线MN的解析式及△OMN的面积.25. 如图1,在Rt△ABC中,∠C=90°,O为斜边AB上一点,以O为圆心、OA为半径的圆恰好与BC相切于点D , 与AB的另一个交点为E , 连接DE .
(1)、若点M是AB边的中点,求反比例函数y= 的解析式和点N的坐标;(2)、若AM=2,求直线MN的解析式及△OMN的面积.25. 如图1,在Rt△ABC中,∠C=90°,O为斜边AB上一点,以O为圆心、OA为半径的圆恰好与BC相切于点D , 与AB的另一个交点为E , 连接DE . (1)、请找出图中与△ADE相似的三角形,并说明理由;(2)、若AC=3,AE=4,试求图中阴影部分的面积;(3)、小明在解题过程中思考这样一个问题:图1中的⊙O的圆心究竟是怎么确定的呢?请你在图2中利用直尺和圆规找到正确圆心O , 并写出你的作图方法.26. 小明大学毕业回家乡创业,第一期培植盆景与花卉各50盆.售后统计,盆景的平均每盆利润是160元,花卉的平均每盆利润是19元.调研发现:
(1)、请找出图中与△ADE相似的三角形,并说明理由;(2)、若AC=3,AE=4,试求图中阴影部分的面积;(3)、小明在解题过程中思考这样一个问题:图1中的⊙O的圆心究竟是怎么确定的呢?请你在图2中利用直尺和圆规找到正确圆心O , 并写出你的作图方法.26. 小明大学毕业回家乡创业,第一期培植盆景与花卉各50盆.售后统计,盆景的平均每盆利润是160元,花卉的平均每盆利润是19元.调研发现:①盆景每增加1盆,盆景的平均每盆利润减少2元;每减少1盆,盆景的平均每盆利润增加2元;
②花卉的平均每盆利润始终不变.
小明计划第二期培植盆景与花卉共100盆,设培植的盆景比第一期增加x盆,第二期盆景与花卉售完后的利润分别为W1 , W2(单位:元).
(1)、用含x的代数式分别表示W1 , W2;(2)、当x取何值时,第二期培植的盆景与花卉售完后获得的总利润W最大,最大总利润是多少?