福建省南平市2019年中考数学一模考试试卷
试卷更新日期:2020-04-21 类型:中考模拟
一、选择题
-
1. 有理数6的相反数是( )A、﹣6 B、6 C、 D、﹣2. 下列图形既是轴对称图形,又是中心对称图形的是( )A、三角形 B、菱形 C、角 D、平行四边形3. 小说《流浪地球》中提到“华北794号地球发动机,全功率运行时能向大地产生1500000000吨的推力”,这里的数据15000000000科学记数法表示为( )A、1.5×1012 B、1.5×1011 C、1.5×1010 D、150×1084. 如图,在⊙O中,∠ACB=34°,则∠AOB的度数是( )
 A、17° B、34° C、56° D、68°5. 中国人最先使用负数,魏晋时期的数学家刘徽在“正负术”的注文中指出,可将算筹(小棍形状的记数工具)正放表示正数,斜放表示负数.如图,根据刘徽的这种表示法,观察图①,可推算图②中所得的数值为( )
A、17° B、34° C、56° D、68°5. 中国人最先使用负数,魏晋时期的数学家刘徽在“正负术”的注文中指出,可将算筹(小棍形状的记数工具)正放表示正数,斜放表示负数.如图,根据刘徽的这种表示法,观察图①,可推算图②中所得的数值为( ) A、﹣3 B、﹣2 C、﹣6 D、+66. 下列说法正确是( )A、了解某型导弹杀伤力的情况应使用全面调查 B、一组数据3、6、6、7、9的众数是6 C、从2000名学生中选200名学生进行抽样调查,样本容量为2000 D、甲、乙两人在相同的条件下各射击10次,他们成绩的平均数相同,方差分别是S2甲=0.3,S2乙=0.4,则乙的成绩更稳定7. 如图,直线AB∥CD , MN分别与AB、CD交于点E、F , 且∠AEM=50°,则∠DFN的大小为( )
A、﹣3 B、﹣2 C、﹣6 D、+66. 下列说法正确是( )A、了解某型导弹杀伤力的情况应使用全面调查 B、一组数据3、6、6、7、9的众数是6 C、从2000名学生中选200名学生进行抽样调查,样本容量为2000 D、甲、乙两人在相同的条件下各射击10次,他们成绩的平均数相同,方差分别是S2甲=0.3,S2乙=0.4,则乙的成绩更稳定7. 如图,直线AB∥CD , MN分别与AB、CD交于点E、F , 且∠AEM=50°,则∠DFN的大小为( ) A、130° B、60° C、50° D、40°8. 如图,在等腰直角△ABC中,∠ACB=90°,D为△ABC内一点,将线段CD绕点C逆时针旋转90°后得到CE , 连接BE , 若∠DAB=10°,则∠ABE是( )
A、130° B、60° C、50° D、40°8. 如图,在等腰直角△ABC中,∠ACB=90°,D为△ABC内一点,将线段CD绕点C逆时针旋转90°后得到CE , 连接BE , 若∠DAB=10°,则∠ABE是( )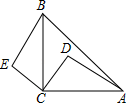 A、75° B、78° C、80° D、92°9. 现有甲,乙两种机器人都被用来搬运某体育馆室内装潢材料甲型机器人比乙型机器人每小时少搬运30千克,甲型机器人搬运600千克所用的时间与乙型机器人搬运800千克所用的时间相同,两种机器人每小时分别搬运多少千克?设甲型机器人每小时搬运x千克,根据题意,可列方程为( )A、 = B、 = C、 = D、 =10. 如图,在△ABC中,AB=AC , BC=6,E为AC边上的点且AE=2EC , 点D在BC边上且满足BD=DE , 设BD=y , S△ABC=x , 则y与x的函数关系式为( )
A、75° B、78° C、80° D、92°9. 现有甲,乙两种机器人都被用来搬运某体育馆室内装潢材料甲型机器人比乙型机器人每小时少搬运30千克,甲型机器人搬运600千克所用的时间与乙型机器人搬运800千克所用的时间相同,两种机器人每小时分别搬运多少千克?设甲型机器人每小时搬运x千克,根据题意,可列方程为( )A、 = B、 = C、 = D、 =10. 如图,在△ABC中,AB=AC , BC=6,E为AC边上的点且AE=2EC , 点D在BC边上且满足BD=DE , 设BD=y , S△ABC=x , 则y与x的函数关系式为( )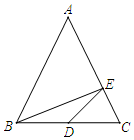 A、y= x2+ B、y= x2+ C、y= x2+2 D、y= x2+2
A、y= x2+ B、y= x2+ C、y= x2+2 D、y= x2+2二、填空题:本题共6小题,每小题4分,共24分
-
11. 分解因式:x2+x= .12. 请写出一个比1大且比3小的无理数: .13. 一个多边形的内角和是720°,这个多边形的边数是 .14. 已知扇形的弧长为4π,半径为8,则此扇形的面积为 .15. n个数据2、4、6、8、….、2n , 这组数据的中位数是 . (用含n的代数式表示)16. 已知,Rt△ABC中,∠ACB=90°,AC=5,BC=12,点D在边AB上,以AD为直径的⊙O , 与边BC有公共点E , 则AD的最小值是 .
三、解答题
-
17. 计算:2sin30°﹣(π﹣ )0+| ﹣1|+( )﹣118. 解不等式组:19. 如图,▱ABCD的对角线ACBD有相交于点O,且E、F、G、H分别是OA、OB、OC、OD的中点.求证:四边形EFGH是平行四边形.
 20. 某校开展以“学习朱子文化,弘扬理学思想”为主题的读书月活动,并向学生征集读后感,学校将收到的读后感篇数按年级进行统计,绘制了以下两幅统计图(不完整).
20. 某校开展以“学习朱子文化,弘扬理学思想”为主题的读书月活动,并向学生征集读后感,学校将收到的读后感篇数按年级进行统计,绘制了以下两幅统计图(不完整).
据图中提供的信息完成以下问题
(1)、扇形统计图中“八年级”对应的圆心角是°,并补全条形统计图;(2)、经过评审,全校有4篇读后感荣获特等奖,其中有一篇来自七年级,学校准备从特等奖读后感中任选两篇在校广播电台上播出,请利用画树状图或列表的方法求出七年级特等奖读后感被校广播电台播出的概率.21. 如图,AE∥BF , AC平分∠BAE , 交BF于点C . (1)、求证:AB=BC;(2)、尺规作图:在AE上找一点D , 使得四边形ABCD为菱形(不写作法,保留作图痕迹)22. 如图,已知反比例函数y= 的图象经过第一象限内的一点A(n , 4),过点A作AB⊥x轴于点B , 且△AOB的面积为2.
(1)、求证:AB=BC;(2)、尺规作图:在AE上找一点D , 使得四边形ABCD为菱形(不写作法,保留作图痕迹)22. 如图,已知反比例函数y= 的图象经过第一象限内的一点A(n , 4),过点A作AB⊥x轴于点B , 且△AOB的面积为2. (1)、求m和n的值;(2)、若一次函数y=kx+2的图象经过点A , 并且与x轴相交于点C , 求线段AC的长.23. 列方程(组)解应用题
(1)、求m和n的值;(2)、若一次函数y=kx+2的图象经过点A , 并且与x轴相交于点C , 求线段AC的长.23. 列方程(组)解应用题打折前,买60件A商品和30件B商品用了1080元,买50件A商品和10件B商品用了840元.打折后,买500件A商品和500件B商品用了9600元,比不打折少花费多少钱?
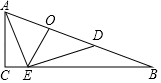
24. 如图,OA是⊙O的半径,点E为圆内一点,且OA⊥OE , AB是⊙O的切线,EB交⊙O于点F , BQ⊥AF于点Q . (1)、如图1,求证:OE∥AB;(2)、如图2,若AB=AO , 求 的值;(3)、如图3,连接OF , ∠EOF的平分线交射线AF于点P , 若OA=2,cos∠PAB= ,求OP的长.25. 已知m , n分别是关于x的一元二次方程ax2+bx+c=a与ax2+bx+c=b的一个根,且m=n+1.(1)、当m=2,a=﹣1时,求b与c的值;(2)、用只含字母a , n的代数式表示b;(3)、当a<0时,函数y=ax2+bx+c满足b2﹣4ac=a , b+c≥2a , n≤﹣ ,求a的取值范围.
(1)、如图1,求证:OE∥AB;(2)、如图2,若AB=AO , 求 的值;(3)、如图3,连接OF , ∠EOF的平分线交射线AF于点P , 若OA=2,cos∠PAB= ,求OP的长.25. 已知m , n分别是关于x的一元二次方程ax2+bx+c=a与ax2+bx+c=b的一个根,且m=n+1.(1)、当m=2,a=﹣1时,求b与c的值;(2)、用只含字母a , n的代数式表示b;(3)、当a<0时,函数y=ax2+bx+c满足b2﹣4ac=a , b+c≥2a , n≤﹣ ,求a的取值范围.