福建省龙岩市2019年中考数学一模考试试卷
试卷更新日期:2020-04-21 类型:中考模拟
一、选择题
-
1. 如图,数轴上的单位长度为1,若实数a , b所表示的数恰好在整数点上,则a+b=( )
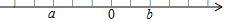 A、0 B、﹣1 C、1 D、52. 下列所给的汽车标志图案中,既是轴对称图形,又是中心对称图形的是( )A、
A、0 B、﹣1 C、1 D、52. 下列所给的汽车标志图案中,既是轴对称图形,又是中心对称图形的是( )A、 B、
B、 C、
C、 D、
D、 3. 下列调查中,适合采用全面调查(普查)方式的是( )A、对长江水质情况的调查 B、对端午节期间市场上粽子质量情况的调查 C、对某班40名同学体重情况的调查 D、对某类烟花爆竹燃放安全情况的调查4. 是 方程组 的解,则5a﹣b的值是( )A、10 B、﹣10 C、14 D、215. 下列图形中,∠1一定大于∠2的是( )A、
3. 下列调查中,适合采用全面调查(普查)方式的是( )A、对长江水质情况的调查 B、对端午节期间市场上粽子质量情况的调查 C、对某班40名同学体重情况的调查 D、对某类烟花爆竹燃放安全情况的调查4. 是 方程组 的解,则5a﹣b的值是( )A、10 B、﹣10 C、14 D、215. 下列图形中,∠1一定大于∠2的是( )A、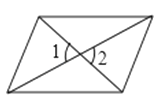 B、
B、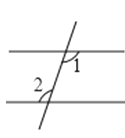 C、
C、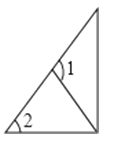 D、
D、 6. 若关于x的一元一次不等式组 的解集是x<5,则m的取值范围是( )A、m≥5 B、m>5 C、m≤5 D、m<57. 如图,x、y、z分别表示以直角三角形三边为边长的正方形面积,则下列结论正确是( )
6. 若关于x的一元一次不等式组 的解集是x<5,则m的取值范围是( )A、m≥5 B、m>5 C、m≤5 D、m<57. 如图,x、y、z分别表示以直角三角形三边为边长的正方形面积,则下列结论正确是( )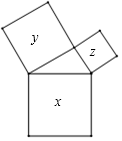 A、x2=y2+z2 B、x<y+z C、x﹣y>z D、x=y+z8. 三个等边三角形的摆放位置如图,若∠3=60°,则∠1+∠2的度数为( )
A、x2=y2+z2 B、x<y+z C、x﹣y>z D、x=y+z8. 三个等边三角形的摆放位置如图,若∠3=60°,则∠1+∠2的度数为( )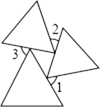 A、90° B、120° C、270° D、360°9. 如图,抛物线y=ax2+bx+c与x轴交于点A(﹣1,0),顶点坐标是(1,n),与y轴的交点在(0,3)和(0,6)之间(包含端点),则下列结论不正确是( )
A、90° B、120° C、270° D、360°9. 如图,抛物线y=ax2+bx+c与x轴交于点A(﹣1,0),顶点坐标是(1,n),与y轴的交点在(0,3)和(0,6)之间(包含端点),则下列结论不正确是( ) A、3a+b<0 B、﹣2≤a≤﹣1 C、abc>0 D、9a+3b+2c>010. 某些整数的所有正约数之和可以按如下方法求得,如:
A、3a+b<0 B、﹣2≤a≤﹣1 C、abc>0 D、9a+3b+2c>010. 某些整数的所有正约数之和可以按如下方法求得,如:6=2×3,则6的所有正约数之和为(1+3)+(2+6)=(1+2)×(1+3)=12;
12=22×3,则12的所有正约数之和为(1+3)+(2+6)+(4+12)=(1+2+22)×(1+3)=28
36=22×32 , 则36的所有正约数之和为(1+3+9)+(2+6+18)+(4+12+36)=(1+2+22)×(1+3+32)=91
参照上述方法,那么144的所有正约数之和为( )
A、424 B、421 C、420 D、403二、填空题:本大题共6小题,每小题4分,共24分
-
11. (﹣2)﹣1= .12. 一个不透明的袋子中装有4个黑球,2个白球,每个球除颜色外其他都相同,从中任意摸出1个球是白球的概率是 .13. 已知α是锐角,且sinα= ,则cosα= .14. 当x=a与x=b(a≠b)时,代数式x2﹣2x+3的值相等,则x=a+b时,代数式x2﹣2x+3的值为 .15. 如图,AB是⊙O的直径,点E是 的中点,连接AF交过E的切线于点D , AB的延长线交该切线于点C , 若∠C=30°,⊙O的半径是2,则图形中阴影部分的面积是 .
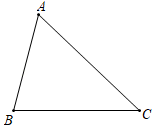
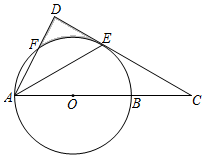 16. 如图,△ABC中,∠ABC=30°,AB=4,BC=5,P是△ABC内部的任意一点,连接PA , PB , PC , 则PA+PB+PC的最小值为 .
16. 如图,△ABC中,∠ABC=30°,AB=4,BC=5,P是△ABC内部的任意一点,连接PA , PB , PC , 则PA+PB+PC的最小值为 .
三、解答题:本大题共9小题,共86分.
-
17. 解方程: ﹣ =1.18. 先化简,再求值: ÷(x﹣ ),其中x= .19. 在四边形ABCD中,AB∥CD .
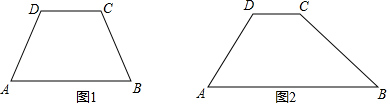 (1)、如图1,已知∠A=∠B , 求证:AD=BC;(2)、如图2,已知∠A=60°,∠B=45°,AD=2,求BC的长.20. 证明:三角形的中位线平行于三角形的第三边,并且等于第三边的一半.
(1)、如图1,已知∠A=∠B , 求证:AD=BC;(2)、如图2,已知∠A=60°,∠B=45°,AD=2,求BC的长.20. 证明:三角形的中位线平行于三角形的第三边,并且等于第三边的一半.(要求:在给出的△ABC中用尺规作出AB、AC边的中点M、N , 保留作图痕迹,不要求写作法,并根据图形写出已知、求证和证明)
 21.(1)、计算: + + + +(2)、求证: < + + + <22. 小宝大学毕业后回家乡透行园艺创业,第一期培植盆景与花卉各50盆,售后进行统计得知:盆景的平均每盆利润是160元,花卉的平均每盆利润是20元.调研发现:①盆景每增加1盆,盆景的平均每盆利润减少2元:每减少1盆,盆景的平均每盆利润增加2元;②花卉的平均际盆利润始终不变,小宝计划第二期培植盆景与花卉共100盆,设培植的盆景比第一期增加x盆,第二期盆景与花卉售完后的利润分别为W1、W2(单位:元)(1)、用含x的代数式分别表示W1、W2;(2)、当x取何值时,第二期培植的盆景与花卉作售完行获得的总利润最大?最大总利润是多少?23. 随着互联网、移动终端的迅速发展,数字化阅读越来越普及.公交、地铁上的“低头族”越来越多,某研究机构针对“您如何看待数字化阅读”问题进行了随机问卷调查(问卷训查表如下图所示),并将调查结果绘制成图①和图②所示的统计图(均不完整).
21.(1)、计算: + + + +(2)、求证: < + + + <22. 小宝大学毕业后回家乡透行园艺创业,第一期培植盆景与花卉各50盆,售后进行统计得知:盆景的平均每盆利润是160元,花卉的平均每盆利润是20元.调研发现:①盆景每增加1盆,盆景的平均每盆利润减少2元:每减少1盆,盆景的平均每盆利润增加2元;②花卉的平均际盆利润始终不变,小宝计划第二期培植盆景与花卉共100盆,设培植的盆景比第一期增加x盆,第二期盆景与花卉售完后的利润分别为W1、W2(单位:元)(1)、用含x的代数式分别表示W1、W2;(2)、当x取何值时,第二期培植的盆景与花卉作售完行获得的总利润最大?最大总利润是多少?23. 随着互联网、移动终端的迅速发展,数字化阅读越来越普及.公交、地铁上的“低头族”越来越多,某研究机构针对“您如何看待数字化阅读”问题进行了随机问卷调查(问卷训查表如下图所示),并将调查结果绘制成图①和图②所示的统计图(均不完整).“您如何看待教化阅读”问卷调查表
您好!这是一份关于“您如何看待数字化间读问调查表,请在表格中选择一项您最认观点,在其后空格内打“√”,非常感谢您的合作.
代码
观点
A
获取信息方便,可以随时随地观看
B
价格便宜易得
C
使得人们成为“低头族”,不利于
人际交往
D
内容丰富,比低纸质书涉猎更广
E
其他
请根据统计图中提供的信息,解答下列问题:
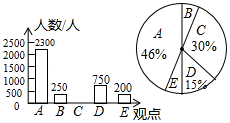 (1)、本次接受词查的总人数是人,并将条形统计图补充完整;(2)、在扇形统计图中,观点E的百分比是 , 表示观点B的扇形的圆心角度数为度.(3)、某市共有300万人,请根据以上调查结果估算该市持A、B、D观点赞成数字化阅读的人数共有多少万人.24. 如图,点P是⊙O直径AB上的一点,过P作直线CD⊥AB , 分别交⊙O于C、D两点,连接AC , 并将线段AC绕点A进时针旋转90°得到AE , 连接ED , 分别交⊙O和AB于F、G , 连接FC .
(1)、本次接受词查的总人数是人,并将条形统计图补充完整;(2)、在扇形统计图中,观点E的百分比是 , 表示观点B的扇形的圆心角度数为度.(3)、某市共有300万人,请根据以上调查结果估算该市持A、B、D观点赞成数字化阅读的人数共有多少万人.24. 如图,点P是⊙O直径AB上的一点,过P作直线CD⊥AB , 分别交⊙O于C、D两点,连接AC , 并将线段AC绕点A进时针旋转90°得到AE , 连接ED , 分别交⊙O和AB于F、G , 连接FC .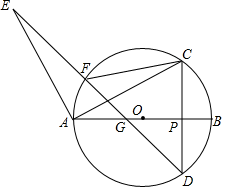 (1)、求证:∠ACF=∠AED;(2)、若点P在直径AB上运动(不与点A、B重合),其它条件不变,请问 是否为定值?若是,请求出其值;若不是,请说明理由.25. 已知直线y=x+t与双曲线y= (k>0)交于C、D两点,过C作CA⊥x轴于点A , 过D作DB⊥y轴于点B , 连接AB .
(1)、求证:∠ACF=∠AED;(2)、若点P在直径AB上运动(不与点A、B重合),其它条件不变,请问 是否为定值?若是,请求出其值;若不是,请说明理由.25. 已知直线y=x+t与双曲线y= (k>0)交于C、D两点,过C作CA⊥x轴于点A , 过D作DB⊥y轴于点B , 连接AB .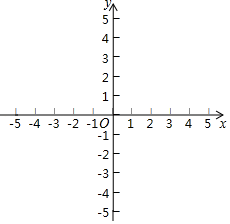 (1)、求C、D两点的坐标;(2)、试探究直线AB与CD的位置关系并说明理由;(3)、已加点D(3,2),且C、D在抛物线y=ax2+bx+5(a≠0)上,若当m≤x≤n(其中mn<0)时,函数y=ax2+bx+5的最小值为2m , 最大值为2n , 求m+n的值.
(1)、求C、D两点的坐标;(2)、试探究直线AB与CD的位置关系并说明理由;(3)、已加点D(3,2),且C、D在抛物线y=ax2+bx+5(a≠0)上,若当m≤x≤n(其中mn<0)时,函数y=ax2+bx+5的最小值为2m , 最大值为2n , 求m+n的值.