河南省安阳市殷都区2019-2020学年八年级上学期数学期中考试试卷
试卷更新日期：2020-04-20 类型：期中考试
一、单选题
-
1. 已知四组线段的长分别如下，以各组线段为边，能组成三角形的是（ ）A、1，2，3 B、2，5，8 C、3，4，5 D、4，5，102. 如图，AB∥CD，∠A+∠E=75°，则∠C为（ ）
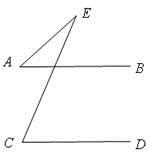A、60 ° B、65 ° C、75 ° D、80 °3. 如图所示，AB＝AC，要说明△ADC≌△AEB，需添加的条件不能是（ ）
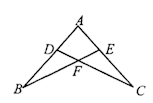A、∠B＝∠C B、AD＝AE C、DC＝BE D、∠ADC＝∠AEB4. 如图，AB∥CD，BP和CP分别平分∠ABC和∠DCB，AD过点P，且与AB垂直．若AD=8，则点P到BC的距离是（ ）
A、8 B、6 C、4 D、25. 下列轴对称图形中，对称轴条数最少的是（ ）A、等边三角形 B、正方形 C、正六边形 D、圆6. 如图，在△ABC中，BC＝8cm，AB的垂直平分线交AB于点D，交边AC于点E，△BCE的周长等于18cm，则AC的长等于（ ）
A、6cm B、8cm C、10cm D、12cm7. 已知一个等腰三角形内角的度数之比为1：4，则它的顶角的度数为（ ）A、20° B、36° C、120° D、20°或120°8. 点 和 关于 轴对称，则 的值为（ ）A、1 B、－1 C、0 D、无法确定9. 在平面直角坐标系xOy中，已知点A（2，﹣2），在y轴上确定点P，使△AOP为等腰三角形，则符合条件的有（ ）个.A、5 B、4 C、3 D、210. 等腰三角形一腰上的高等于这个三角形一条边长度的一半，则其顶角为（ ）A、30° B、30°或150° C、120°或150° D、30°或120°或150°二、填空题
-
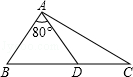
11. 等腰三角形的两边长分别为8cm和3cm，则它的周长为cm．12. 某多边形内角和与外角和共1080°，则这个多边形的边数是.13. 如图，在△ABC中，点D是BC上一点，∠BAD=80°，AB=AD=DC，则∠C=度．
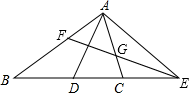
14. 如图，已知△ABC中，∠ABC=45°，F是高AD和BE的交点，CD=4，则线段DF的长是.
15. 如图，已知点 是高为2的等边 的中线 上的动点， 是 边的中点，则 的最小值是.
三、解答题
-
16. 已知 、 、 为 的三边长， 、 满足 ，且 为方程 的解，求 的周长.并判断 的形状.17. 如图， 是 的 边上的高， 是 的一条角平分线，若 ， .求 和 的度数.
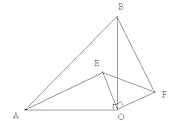
18. 如图，已知四边形ABCD是梯形，AD∥BC，∠A＝90°，BC＝BD，CE⊥BD，垂足为E．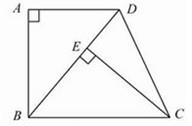
(1)、求证：△ABD≌△ECB；(2)、若∠DBC＝50°，求∠DCE的度数．19. 如果一个多边形的每一个外角都相等，且比内角小 ，求这个多边形的边数和内角和.20. 如图所示， ， ，
(1)、利用关于坐标轴对称的点的坐标的特点，在下面坐标系中作出 关于 轴对称的图形 .(2)、写出 各个顶点的坐标.(3)、求 的面积.
