江苏省南通市海安市八校2019-2020学年八年级上学期数学第三次月考试卷

试卷更新日期：2020-04-20 类型：月考试卷

进入出卷网下载

一、单选题

1. 在平面直角坐标系中，点A，点B关于y轴对称，点A的坐标是（2，-8），则点B的坐标是（）.

A、（-2，-8） B、（2，8） C、（-2，8） D、（8，2）

查看试题解析
2. 某种细胞的直径是0. 00000024m，将0. 00000024用科学记数法表示为（）

A、 $2.4 \times 10^{- 7}$ B、 $2.4 \times 10^{- 8}$ C、 $0.24 \times 10^{- 7}$ D、 $24 \times 10^{- 8}$

查看试题解析
3. 下列各式从左到右的变形，属于因式分解的是（）

A、 $x^{2} - 2 x + 1 = x (x - 2) + 1$ B、 $x^{2} - x y + y^{2} = {(x - y)}^{2}$ C、 $\frac{1}{x^{2}} - \frac{1}{y^{4}} = (\frac{1}{x} + \frac{1}{y^{2}}) (\frac{1}{x} - \frac{1}{y^{2}})$ D、 $x^{4} - 16 = (x^{2} + 4) (x + 2) (x - 2)$

查看试题解析
4. 已知 $a = {(- 5)}^{2} ， b = {(- 5)}^{- 1} ， c = {(- 5)}^{0}$ ，那么 $a ， b ， c$ 之间的大小关系是（）

A、 $a > b > c$ B、 $a > c > b$ C、 $c > b > a$ D、 $c > a > b$

查看试题解析
5. 如果 $(x^{2} + m x + n) (x + 2)$ 的乘积不含 $x^{2}$ 和 $x$ 项，那么 $m, n$ 的值分别是（）

A、 $m = - 2, n = 4$ B、 $m = - 2, n = - 4$ C、 $m = 2, n = - 4$ D、 $m = 2, n = 4$

查看试题解析
6. 在三角形的内部，有一个点到三角形三个顶点的距离相等，则这个点一定是三角形（）

A、三条中线的交点 B、三条角平分线的交点 C、三条边的垂直平分线的交点 D、三条高的交点

查看试题解析
7. 已知x+y﹣3＝0，则2^x×2^y的值为（）

A、64 B、8 C、6 D、12

查看试题解析
8. 如图，在 $△ ABC$ 中，DE是AB的垂直平分线，且分别交AB、AC于点D和E， $∠ A$ =50°， $∠ C$ =60°，则 $∠ EBC$ 为（）

A、30° B、20° C、25° D、35°

查看试题解析
9. 如图， $Δ A B C$ 中， $A B = 6 ， A C = 4$ ， $A D$ 平分 $∠ B A C$ ， $D E ⊥ A B$ 于点 $E$ ， $B F ⊥ A C$ 于点 $F$ ， $D E = 2$ ，则 $B F$ 的长为（）

A、3 B、4 C、5 D、6

查看试题解析
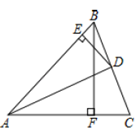10. 已知 $M = 3 (2^{2} + 1) (2^{4} + 1) (2^{8} + 1) (2^{16} + 1)$ ，则 $M$ 的个位数字为（）

A、1 B、3 C、5 D、7

查看试题解析

二、填空题

11. 要使分式 $\frac{2 x}{x - 3}$ 有意义，则 $x$ 须满足的条件为 .

查看试题解析
12. 已知点 $A (- 2, 3)$ 和 $B (2, - 2)$ ，将点 $A$ 向平移个单位长度后得到的点与 $B$ 点关于 $y$ 轴对称.

查看试题解析
13. 如果等腰三角形的一边长为6 cm，周长为14 cm，那么另外两边的长分别为.

查看试题解析
14. 多项式 $x^{2} + m x + 6$ 分解因式得 $(x + 2) (x + n)$ ，则 $m =$ .

查看试题解析
15. 不改变分式的值，使分子、分母各项的系数都化为整数，则 $\frac{0.5 x + 0.7 y}{2 x - 0.6 y} =$ .

查看试题解析
16. 已知 $x + y = 5, x y = - 5$ ，则 $x^{2} + y^{2} =$ .

查看试题解析
17. 如图， $A D ⊥ B C$ 于点 $D$ ， $D$ 为 $B C$ 的中点，连接 $A B ， ∠ A B C$ 的平分线交 $A D$ 于点 $O$ ，连结 $O C$ ，若 $∠ A O C = 125 °$ ，则 $∠ A B C =$ .

查看试题解析
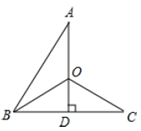18. 如图，在△PAB中，PA=PB，M、N、K分别是PA、PB、AB上的点，且AM= BK ，BN=AK.若∠MKN=50°，则∠P的度数为.

查看试题解析

三、解答题

19. 因式分解：

(1)、 $3 x (x - 2) - (2 - x)$ ；

(2)、 $x^{3} - 16 x$ ；

(3)、 $- 6 a + 9 a^{2} + 1$ ；

(4)、 $x^{4} - 2 x^{2} + 1$ .

查看试题解析
20. 计算：

(1)、 ${(y^{2})}^{3} \div y^{6} \cdot y$ ；

(2)、 $y^{4} + {(y^{2})}^{4} \div y^{4} - {(- y^{2})}^{2}$ ；

(3)、 $\frac{2 m - n}{n - m} + \frac{m}{m - n} + \frac{n}{n - m}$ ；

(4)、 $\frac{1}{x - 1} - \frac{1}{x + 1} - \frac{2}{x^{2} + 1}$ .

查看试题解析
21. 在 $Δ A B C$ 中， $∠ A - ∠ B = 30 °, ∠ C = 4 ∠ B$ ，求 $∠ A 、 ∠ B 、 ∠ C$ 的度数.

查看试题解析
22. 如图，在平面直角坐标系中， $Δ A B C$ 的顶点 $A(0，1)，$ $B(3，2)$ ， $C(2，3)$ 均在正方形网格的格点上.

(1)、画出 $Δ A B C$ 关于 $x$ 轴对称的图形 $Δ A_{1} B_{1} C_{1}$ 并写出顶点 $A_{1}$ ， $B_{1}$ ， $C_{1}$ 的坐标；

(2)、求 $Δ A_{1} B_{1} C_{1}$ 的面积.

查看试题解析
23. 小马、小虎两人共同计算一道题：（x+a）（2x+b）.由于小马抄错了a的符号，得到的结果是2x²﹣7x+3，小虎漏抄了第二个多项式中x的系数得到的结果是x²+2x﹣3.

(1)、求a，b的值；

(2)、细心的你请计算这道题的正确结果；

(3)、当x＝﹣1时，计算（2）中的代数式的值.

查看试题解析
24. 如图，在 $Δ A B C$ 中，已知点 $D$ 在线段 $A B$ 的反向延长线上，过 $A C$ 的中点 $F$ 作线段 $G E$ 交 $∠ D A C$ 的平分线于 $E$ ，交 $B C$ 于 $G$ ，且 $A E ∕ ∕ B C$ .

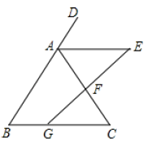(1)、求证： $Δ A B C$ 是等腰三角形；

(2)、若 $A E = 8 c m ， A B = 11 c m ， G C = 2 B G$ ，求 $Δ A B C$ 的周长.

查看试题解析
25. 规定两数 $a, b$ 之间的一种运算，记作 $(a, b)$ ：如果 $a^{c} = b$ ，那么 $(a, b) = c$ . 例如：因为 $2^{3} = 8$ ，所以 $(2, 8) = 3$ .

(1)、根据上述规定，填空： $(5, 25) =$ ， $(5, 1) =$ ， $(3, \frac{1}{9}) =$ .

(2)、小明在研究这种运算时发现一个特征： $(3^{n}, 4^{n}) = (3, 4)$ ，
小明给出了如下的证明：

设 $(3^{n}, 4^{n}) = x$ ，则 ${(3^{n})}^{x} = 4^{n}$ ，即 ${(3^{x})}^{n} = 4^{n}$ ，

所以 $3^{x} = 4$ ，即 $(3, 4) = x$ ，

所以 $(3^{n}, 4^{n}) = (3, 4)$ .

试解决下列问题：

①计算 $(8, 1000) - (32, 100000)$ ；

②请你尝试运用这种方法证明下面这个等式： $(3, 20) - (3, 4) = (3, 5)$ .

查看试题解析
26. 如图①，在等边三角形ABC中．D是AB边上的动点，以CD为一边，向上作等边三角形EDC．连接AE.

(1)、求证：△DBC≌△EAC

(2)、试说明AE∥BC的理由．

(3)、如图②，当图①中动点D运动到边BA的延长线上时，所作仍为等边三角形，猜想是否仍有AE∥BC?若成立请证明．

查看试题解析
27. 如图一，在平面直角坐标系中， $A (a ， 0)$ 是 $x$ 轴正半轴上一点，C是第四象限一点，CB⊥y轴，交y轴负半轴于b(0，b)，且(a-2)²+|b+3|=0，S_四边形_AOBC=12.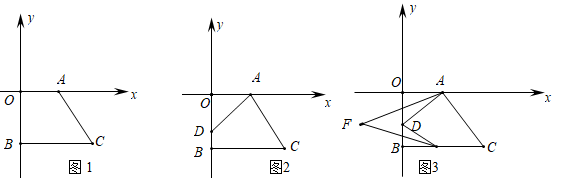

(1)、求C点坐标

(2)、如图二，设D为线段 $OB$ 上一动点(点 $D$ 不与点 $OB$ 重合)，求证：∠ADB+∠DBC-∠OAD=180°

(3)、如图三，当 $D$ 点在线段 $OB$ 上运动(点 $D$ 不与点 $OB$ 重合)， $E$ 点在线段 $BC$ 上运动(点 $E$ 不与点 $B$ 重合)时，连接 $AD$ 、 $DE$ 作∠OAD、∠DEB的平分线交于 $F$ 点，请你探索∠AFE与∠ADE之间的关系，并说明理由.

查看试题解析