浙江省宁波市2019-2020学年数学中考模拟试卷2

试卷更新日期：2020-04-20 类型：中考模拟

进入出卷网下载

一、选择题（每小题4分，共48分，在每小题给出的四个选项中，只有一个符合题目要求）

1. 下面四个数中比﹣2小的数是（）

A、1 B、0 C、﹣1 D、﹣3

查看试题解析
2. 地球距太阳的距离是150000000km，用科学记数法表示为1.5×10ⁿkm，则n的值为（）

A、6 B、7 C、8 D、9

查看试题解析
3. 估算 $\sqrt{27} - 3$ 的值在（　　）

A、1与2之间 B、2与3之间 C、3与4之间 D、5与6之间

查看试题解析
4. 一元二次方程x²﹣8x﹣1=0配方后可变形为（　　）

A、（x+4）²=17 B、（x+4）²=15 C、（x﹣4）²=17 D、（x﹣4）²=15

查看试题解析
5. 某火车站的显示屏，每间隔4分钟显示一次火车班次的信息，显示时间持续1分钟，某人到达该车站时，显示屏上正好显示火车班次信息的概率是（）

A、 $\frac{1}{6}$ B、 $\frac{1}{5}$ C、 $\frac{1}{4}$ D、 $\frac{1}{3}$

查看试题解析
6. 如图是一个正方体包装盒的表面展开图，若在其中的三个正方形A，B，C内分别填上适当的数，使得将这个表面展开图沿虚线折成正方体后，相对面上的两数互为相反数，则填在A，B，C内的三个数依次是（）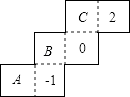

A、1，0，﹣2 B、0，1，﹣2 C、0，﹣2，1 D、﹣2，0，1

查看试题解析
7. 在△ABC中，BC＝a，AB＝c，CA＝b．且a，b，c满足：a²﹣6a＝﹣9，b²﹣8b＝﹣16，c²﹣10c＝﹣25．则2sinA+sinB＝（）

A、1 B、 $\frac{7}{5}$ C、2 D、 $\frac{12}{5}$

查看试题解析
8. 若不等式组 ${\begin{matrix} x + a \geq 0 \\ 1 - 2 x > x - 2 \end{matrix}$ 无解，则实数a的取值范围是（）

A、a≥﹣1 B、a＜﹣1 C、a≤1 D、a≤﹣1

查看试题解析
9. 二次函数y=ax²+bx+c图象上部分点的坐标满足表格：
x
…
﹣3
﹣2
﹣1
0
1
…
y
…
﹣3
﹣2
﹣3
﹣6
﹣11
…
则该函数图象的顶点坐标为（）

A、（﹣3，﹣3） B、（﹣2，﹣2） C、（﹣1，﹣3） D、（0，﹣6）

查看试题解析
10. 如图，将半径为2，圆心角为120°的扇形OAB绕点A逆时针旋转60°，点O，B的对应点分别为O′，B′，连接BB′，则图中阴影部分的面积是（）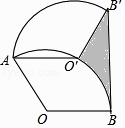

A、 $\frac{2 π}{3}$ B、2 $\sqrt{3}$ ﹣ $\frac{π}{3}$ C、2 $\sqrt{3}$ ﹣ $\frac{2 π}{3}$ D、4 $\sqrt{3}$ ﹣ $\frac{2 π}{3}$

查看试题解析
11. 如图，AB是半圆的直径，点C是弧AB的中点，点E是弧AC的中点，连接EB，CA交于点F，则 $\frac{E F}{B F}$ ＝（）

A、 $\frac{1}{3}$ B、 $\frac{1}{4}$ C、1﹣ $\frac{\sqrt{2}}{2}$ D、 $\frac{\sqrt{2} - 1}{2}$

查看试题解析
12. 一个大正方形内放入两个同样大小的小正方形纸片，按如图1放置，两个小正方形纸片的重叠部分面积为4；按如图2放置（其中一小张正方形居大正方形的正中），大正方形中没有被小正方形覆盖的部分（阴影部分）的面积为44，则把两张小正方形按如图3放置时，两个小正方形重叠部分的面积为（）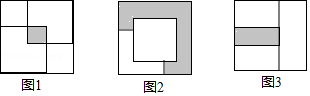

A、11 B、12 C、20 D、24

查看试题解析

二、填空题（每小题4分，共24分）

13. 已知3，a，4，b，5这五个数据，其中a，b是方程x²﹣3x+2＝0的两个根，则这五个数据的标准差是．

查看试题解析
14. 设A（x₁ ， y₁），B（x₂ ， y₂）为函数 $y = \frac{k^{2} - 1}{x}$ 图象上的两点，且x₁＜0＜x₂ ， y₁＞y₂ ，则实数k的取值范围是．

查看试题解析
15. 如图，⊙P的半径为2，圆心P在 $y = \frac{6}{x}$ （x＞0）的图象上运动，当⊙P与x轴相切时，点P的坐标为．

查看试题解析
16. 如图，Rt△ABC中，∠BCA＝90°，∠BAC＝30°，AB＝6．△ABC以点B为中心逆时针旋转，使点C旋转至AB边延长线上的C′处，那么AC边转过的图形（图中阴影部分）的面积是．

查看试题解析
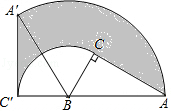17. 如图一张长方形纸片ABCD，其长AD为a，宽AB为b（a＞b），在BC边上选取一点M，将△ABM沿AM翻折后B至B′的位置，若B′为长方形纸片ABCD的对称中心，则 $\frac{a}{b}$ 的值为．

查看试题解析
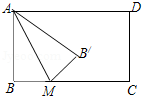18. 如图，正方形ABCD内接于⊙O，E为DC的中点，直线BE交⊙O于点F，如果⊙O的半径为，则O点到BE的距离OM＝．

查看试题解析

三、解答题（本大题有8小题，共78分）

19. 计算： $\sqrt{8}$ ﹣4sin45°+|﹣4|.

查看试题解析
20. 化简 $\frac{a}{a^{2} - 4} \div \frac{a^{2} - 3 a}{a + 2} - \frac{1}{2 - a}$ ，并求值，其中a与2，3构成△ABC的三边，且a为整数．

查看试题解析
21. 为推广阳光体育“大课间”活动，我市某中学决定在学生中开设A：实心球，B：立定跳远，C：跳绳，D：跑步四种活动项目．为了了解学生对四种项目的喜欢情况，随机抽取了部分学生进行调查，并将调查结果绘制成如图①②的统计图．请结合图中的信息解答下列问题：

(1)、在这项调查中，共调查了多少名学生？

(2)、请计算本项调查中喜欢“立定跳远”的学生人数和所占百分比，并将两个统计图补充完整；

(3)、若调查到喜欢“跳绳”的5名学生中有3名男生，2名女生．现从这5名学生中任意抽取2名学生．请用画树状图或列表的方法，求出刚好抽到同性别学生的概率．

查看试题解析
22. 随着互联网的普及，某手机厂商采用先网络预定，然后根据订单量生产手机的方式销售，2015年该厂商将推出一款新手机，根据相关统计数据预测，定价为2200元，日预订量为20000台，若定价每减少100元，则日预订量增加10000台．

(1)、设定价减少x元，预订量为y台，写出y与x的函数关系式；

(2)、若每台手机的成本是1200元，求所获的利润w（元）与x（元）的函数关系式，并说明当定价为多少时所获利润最大；

(3)、若手机加工成每天最多加工50000台，且每批手机会有5%的故障率，通过计算说明每天最多接受的预订量为多少？按最大量接受预订时，每台售价多少元？

查看试题解析
23. 如图所示，某办公大楼正前方有一根高度是15米的旗杆ED，从办公楼顶端A测得旗杆顶端E的俯角α是45°，旗杆底端D到大楼前梯坎底边的距离DC是20米，梯坎坡长BC是12米，梯坎坡度i＝1： $\sqrt{3}$ ，求大楼AB的高度是多少？（精确到0.1米，参考数据： $\sqrt{2}$ ≈1.41， $\sqrt{3}$ ≈1.73， $\sqrt{6}$ ≈2.45）

查看试题解析
24. 如图，⊙O为等腰△ABC的外接圆，直径AB＝12，P为弧 $\overset{⌢}{B C}$ 上任意一点（不与B，C重合），直线CP交AB延长线于点Q，⊙O在点P处切线PD交BQ于点D，

(1)、若PD∥BC，求证：AP平分∠CAB；

(2)、若PB＝BD，求PD的长度；

(3)、证明：无论点P在弧 $\overset{⌢}{B C}$ 上的位置如何变化，CP•CQ为定值．

查看试题解析
25. 如图，在矩形ABCD中，点E是AD边上的一个动点，连接BE，作点A关于BE的对称点F，且点F落在矩形ABCD的内部（不包括边界），连接AF，BF，EF，过点F作GF⊥AF交AD边于点G，设 $\frac{A D}{A B} = t$ .

(1)、求证：AE=GE；

(2)、当点F落在AC上时，用含t的代数式表示 $\frac{A D}{A E}$ 的值；

(3)、若t=3，且以点F，C，G为顶点的三角形是直角三角形，求 $\frac{A D}{A E}$ 的值．

查看试题解析
26. 在平面直角坐标系中，O为原点，点A（1，0），点B（0， $\sqrt{3}$ ），把△ABO绕点O顺时针旋转，得A′B′O，记旋转角为α．

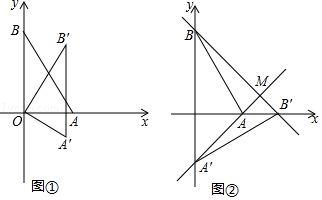(1)、如图①，当α＝30°时，求点B′的坐标；

(2)、设直线AA′与直线BB′相交于点M．
①如图②，当α＝90°时，求点M的坐标；

②点C（﹣1，0），求线段CM长度的最小值．（直接写出结果即可）

查看试题解析

x	…	﹣3	﹣2	﹣1	0	1	…
y	…	﹣3	﹣2	﹣3	﹣6	﹣11	…