云南省玉溪市红塔区2018-2019学年七年级下学期数学期中考试试卷

试卷更新日期：2020-04-20 类型：期中考试

进入出卷网下载

一、单选题

1. 若∠A与∠B是对顶角且互补，则它们两边所在的直线（）

A、互相垂直 B、互相平行 C、既不垂直也不平行 D、不能确定

查看试题解析
2. 4的平方根是（）

A、 ±16 B、2 C、﹣2 D、±2

查看试题解析
3. 在平面直角坐标系中，点(－3， 2)在（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
4. 如图，能判定EB∥AC的条件是（）

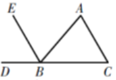A、∠C=∠ABE B、∠A=∠EBD C、∠A=∠ABE D、∠C=∠ABC

查看试题解析
5. 在实数：3.14159， $\sqrt[3]{64}$ ，1.010010001，4.21，π， $\frac{22}{7}$ 中，无理数有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
6. 下列命题是假命题的是（）.

A、同位角相等 B、平行于同一直线的两直线平行 C、在同一平面内，过一点有且只有一条直线与已知直线垂直 D、两直线平行，内错角相等

查看试题解析
7. 已知 ${\begin{array}{l} x = 3 \\ y = - 2 \end{array}$ 是二元一次方程3x﹣my＝5的一组解，则m的值为（）

A、﹣2 B、2 C、﹣ $\frac{1}{2}$ D、 $\frac{1}{2}$

查看试题解析
8. 如果方程组 ${\begin{matrix} x + y = 8 \\ y + z = 6 \\ z + x = 4 \end{matrix}$ 的解使代数式kx+2y﹣3z的值为8，则k=（）

A、 $\frac{1}{3}$ B、﹣ $\frac{1}{3}$ C、3 D、﹣3

查看试题解析

二、填空题

9. 如图，在线段AC，BC，CD中，线段最短，理由是.

查看试题解析
10. 如图，直线AB，CD相交于点O，OE⊥AB，∠COE＝68°，则∠BOD的度数为.

查看试题解析
11. 若一个正数的平方根是2a-3与5-a，则这个正数是.

查看试题解析
12. 点P(2a,1－3a)是第二象限内的一个点，且点P到两坐标轴的距离之和为6，则点P的坐标是.

查看试题解析
13. 已知 ${\begin{matrix} x = 2 \\ y = 1 \end{matrix}$ 是二元一次方程组 ${\begin{matrix} m x + n y = 7 \\ n x - m y = 1 \end{matrix}$ 的解，则m+3n的立方根为．

查看试题解析

三、解答题

14. 计算：

(1)、（﹣2）²× $\sqrt{\frac{1}{4}}$ +| $\sqrt[3]{- 8}$ |+ $\sqrt{2} \times {(- 1)}^{2016}$ ；

(2)、 $\sqrt{81} + \sqrt[3]{- 27} + \sqrt{{(- 2)}^{2}} + | \sqrt{3} - 2 |$ .

查看试题解析
15. 求下列等式中x的值：

(1)、2x²﹣ $\frac{1}{2}$ ＝0；

(2)、（x+4）³＝125.

查看试题解析
16. 已知2a﹣1的平方根是±3，11a+b﹣1的立方根是4，求a+2b的平方根.

查看试题解析
17. 解下列方程组：

(1)、 ${\begin{array}{l} 3 x + 2 y = 19 \\ x - 4 y = 24 \end{array}$ ；

(2)、 ${\begin{array}{l} \frac{x}{3} + \frac{y}{2} = 5 \\ 3 x + 2 y = 25 \end{array}$ .

查看试题解析
18. 如图，直线AB、CD相交于点O，OE把 $∠ BOD$ 分成两部分，

(1)、直接写出图中 $∠ AOC$ 的对顶角为， $∠ BOE$ 的邻补角为；

(2)、若 $∠ AOC = 70 °$ ，且 $∠ BOE ： ∠ EOD$ =2：3，求 $∠ AOE$ 的度数.

查看试题解析
19. 如图，AE⊥BC，FG⊥BC，∠1＝∠2，求证：AB∥CD.

查看试题解析
20. 如图所示，△ABC中，A（﹣2，1）、B（﹣4，﹣2）、C（﹣1，﹣3），△A′B′C′是△ABC平移之后得到的图，并且C的对应点C′的坐标为（4，1）。

(1)、A′、B′.两点的坐标分别为A′、B′；

(2)、请作出△ABC平移之后的图形△A′B′C′；

(3)、求△A′B′C′的面积.

查看试题解析
21. “重百”、“沃尔玛”两家超市出售同样的保温壶和水杯，保温壶和水杯在两家超市的售价分别一样.已知买1个保温壶和1个水杯要花费60元，买2个保温壶和3个水杯要花费130元.

(1)、请问：一个保温壶与一个水杯售价各是多少元；（列方程组求解）

(2)、为了迎接“五一劳动节”，两家超市都在搞促销活动，“重百”超市规定：这两种商品都打九折；“沃尔玛”超市规定：买一个保温壶赠送一个水杯.若某单位想要买4个保温壶和15个水杯，如果只能在一家超市购买，请问选择哪家超市购买更合算，请说明理由.

查看试题解析
22. 如图①，在平面直角坐标系中，点A，B的坐标分别为（﹣1，0），（3，0），现同时将点A，B分别向上平移2个单位长度，再向右平移1个单位长度，分别得到点A，B的对应点C，D，连接AC，BD，CD.

(1)、求点C，D的坐标及S_四边形_ABDC；

(2)、在y轴上是否存在一点Q，连接QA，QB，使S_△_QAB＝S_四边形_ABDC若存在这样一点，求出点Q的坐标；若不存在，试说明理由；

(3)、如图②，点P是线段BD上的一个动点，连接PC，PO，当点P在BD上移动时（不与B，D重合），求证：∠DCP+∠BOP＝∠CPO.

查看试题解析