贵州省遵义市2018-2019学年七年级下学期数学期中考试试卷
试卷更新日期:2020-04-20 类型:期中考试
一、单选题
-
1. 下列所示的图案分别是奔驰、雪铁龙、大众、三菱汽车的车标,其中可以看作由“基本图案”经过平移得到的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列各数: , , ,﹣1.414, , ,0.1010010001…(每相两个1之间依次多一个0)中,无理数有( )A、1个 B、2个 C、3个 D、4个3. 如图,能判定EB∥AC的条件是( )
2. 下列各数: , , ,﹣1.414, , ,0.1010010001…(每相两个1之间依次多一个0)中,无理数有( )A、1个 B、2个 C、3个 D、4个3. 如图,能判定EB∥AC的条件是( ) A、∠C=∠ABE B、∠A=∠EBD C、∠C=∠ABC D、∠A=∠ABE4. 下列说法错误的是( )A、﹣4是16的平方根 B、 的算术平方根是2 C、 的平方根是 D、 =55. 如图,点P是直线a外的一点,点A,B,C在直线a上,且PB⊥a,垂足是B,PA⊥PC,则下列不正确的语句是( )
A、∠C=∠ABE B、∠A=∠EBD C、∠C=∠ABC D、∠A=∠ABE4. 下列说法错误的是( )A、﹣4是16的平方根 B、 的算术平方根是2 C、 的平方根是 D、 =55. 如图,点P是直线a外的一点,点A,B,C在直线a上,且PB⊥a,垂足是B,PA⊥PC,则下列不正确的语句是( ) A、线段PC的长是点C到直线PA的距离 B、线段AC的长是点A到直线PC的距离 C、PA,PB,PC三条线段中,PB最短 D、线段PB的长是点P到直线a的距离6. 下列四个命题中:
A、线段PC的长是点C到直线PA的距离 B、线段AC的长是点A到直线PC的距离 C、PA,PB,PC三条线段中,PB最短 D、线段PB的长是点P到直线a的距离6. 下列四个命题中:①在同一平面内,互相垂直的两条直线一定相交
②有且只有一条直线垂直于已知直线
③两条直线被第三条直线所截,同位角相等
④从直线外一点到这条直线的垂线段,叫做这点到这条直线的距离.
其中真命题的个数为( )
A、1个 B、2 个 C、3个 D、4个7. 若点P(m,1)在第二象限内,则点Q(1﹣m,﹣1)在( )A、x轴负半轴上 B、y轴负半轴上 C、第三象限 D、第四象限8. 若a是(﹣3)2的平方根,则 等于( )A、﹣3 B、 C、 或﹣ D、3或﹣39. 一个长方形在平面直角坐标系中的三个顶点的坐标分别为(-1,-1)、(-1,2)、(3,-1),则第四个顶点的坐标为( )A、(2,2) B、(3,2) C、(3,3) D、(2,3)10. 如图,直线m∥n,Rt△ABC的顶点A在直线n上,∠C=90°,AB,CB分别交直线m于点D和点E,且DB=DE,若∠1=65°,则∠BDE的度数为( ) A、115° B、120° C、130° D、145°11. 在直线MN上取一点P,过点P作射线PA,PB,使PA⊥PB,当∠MPA=40°,则∠NPB的度数是( )A、50° B、60° C、40°或140° D、50°或130°12.
A、115° B、120° C、130° D、145°11. 在直线MN上取一点P,过点P作射线PA,PB,使PA⊥PB,当∠MPA=40°,则∠NPB的度数是( )A、50° B、60° C、40°或140° D、50°或130°12.如图,在平面直角坐标系中,有若干个整数点,其顺序按图中“→”方向排列,如(1,0),(2,0),(2,1),(3,2),(3,1),(3,0),(4,0).根据这个规律探索可得,第100个点的坐标为( )
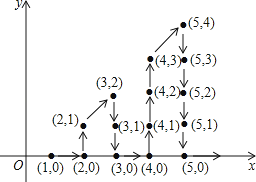 A、(14,8) B、(13,0) C、(100,99) D、(15,14)
A、(14,8) B、(13,0) C、(100,99) D、(15,14)二、填空题
-
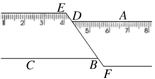
13. 比较大小: 2(填“<”、“>”、或“=”).14. 如图,一把矩形直尺沿直线断开并错位,点E、D、B、F在同一条直线上,若∠ADE=125°, 则∠DBC的度数为 .
 15. 已知|a﹣2|+ =0,则ba=.16. 已知:如图,CD平分∠ACB,∠1+∠2=180°,∠3=∠A,∠4=35°,则∠CED=.
15. 已知|a﹣2|+ =0,则ba=.16. 已知:如图,CD平分∠ACB,∠1+∠2=180°,∠3=∠A,∠4=35°,则∠CED=.
三、解答题
-
17. 计算:﹣12019+|(﹣2)3﹣10|×( +0.5)﹣ .18. 解方程:(1)、(x﹣3)2+1=26;(2)、 ﹣ =1.19. 三角形ABC与三角形 在平面直角坐标系中的位置如图所示,三角形 是由三角形ABC经过平移得到的.
 (1)、分别写出点 的坐标;(2)、说明三角形 是由三角形ABC经过怎样的平移得到的;(3)、若点 是三角形ABC内的一点,则平移后点P在三角形 内的对应点为P‘,写出点P’的坐标.20. 已知2a﹣1的算术平方根是3,b﹣1是 的整数部分,c+1和9的平方根相等,求a﹣2b﹣c的值.21. 推理填空
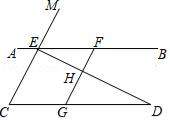
(1)、分别写出点 的坐标;(2)、说明三角形 是由三角形ABC经过怎样的平移得到的;(3)、若点 是三角形ABC内的一点,则平移后点P在三角形 内的对应点为P‘,写出点P’的坐标.20. 已知2a﹣1的算术平方根是3,b﹣1是 的整数部分,c+1和9的平方根相等,求a﹣2b﹣c的值.21. 推理填空如图:∠ABC=∠ACB,BD平分∠ABC,CE平分∠ACB,∠DBF=∠F,求证:CE∥DF.请完成下面的解题过程.

解:∵BD平分∠ABC,CE平分∠ACB ( 已知 )
∴∠DBC= ∠_▲_,∠ECB= ∠_▲_( 角平分线的定义)
又∵∠ABC=∠ACB (已知)
∴∠_▲_=∠_▲_.
又∵∠_▲_=∠_▲_ (已知)
∴∠F=∠_▲_
∴CE∥DF_▲__.
22. 小丽想在一块面积为640cm2的正方形纸片中,沿着边的方向裁出一块面积为420cm2的长方形的纸片,使它的长与宽之比为3:2,小丽能用这块纸片裁出符合要求的纸片吗?请简要说明理由.23. 阅读下面文字,然后回答问题.大家知道 是无理数,而无理数是无限不循环小数,所以 的小数部分我们不可能全部写出来,由于 的整数部分是1,将 减去它的整数部分,差就是它的小数部分,因此 的小数部分可用 ﹣1表示.
由此我们得到一个真命题:如果 =x+y,其中x是整数,且0<y<1,那么x=1,y= ﹣1.
请解答下列问题:
(1)、如果 =a+b,其中a是整数,且0<b<1,那么a= , b=;(2)、如果﹣ =c+d,其中c是整数,且0<d<1,那么c= , d=;(3)、已知2+ =m+n,其中m是整数,且0<n<1,求|m﹣n|的值.