江苏省镇江市润州区2019届九年级下学期数学期中考试试卷
试卷更新日期:2020-04-20 类型:期中考试
一、单选题
-
1. 我国倡导的“一带一路”建设将促进我国与世界一些国家的互利合作,根据规划“一带一路”地区覆盖总 人口为4400000000人,这个数用科学记数法表示为( )A、4.4×108 B、4.40×108 C、4.4×109 D、4.4×10102. 在一次中学生田径运动会上,参加跳远的15名运动员的成绩如下表所示

则这些运动员成绩的中位数、众数分别是( )
A、4.65、4.70 B、4.65、4.75 C、4.70、4.75 D、4.70、4.703. 如图,正六边形ABCDEF内接于⊙O,半径为4,则这个正六边形的边心距OM和 的长分别为( )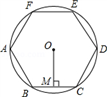 A、2, B、2 ,π C、 , D、2 ,4. 如图,已知点A(-8,0)、B(2,0),点C在直线y=-0.75x+4上,则使△ABC是直角三角形的点C的个数为( )
A、2, B、2 ,π C、 , D、2 ,4. 如图,已知点A(-8,0)、B(2,0),点C在直线y=-0.75x+4上,则使△ABC是直角三角形的点C的个数为( ) A、1 B、2 C、3 D、45. 如图是二次函数y=ax2+bx+c(a,b,c是常数,a≠0)图象的一部分,与x轴的交点A在点(2,0)和(3,0)之间,对称轴是x=1.对于下列说法:①ab<0;②2a+b=0;③3a+c>0;④a+b≥m(am+b)(m为实数);⑤当﹣1<x<3时,y>0,其中正确的是( )
A、1 B、2 C、3 D、45. 如图是二次函数y=ax2+bx+c(a,b,c是常数,a≠0)图象的一部分,与x轴的交点A在点(2,0)和(3,0)之间,对称轴是x=1.对于下列说法:①ab<0;②2a+b=0;③3a+c>0;④a+b≥m(am+b)(m为实数);⑤当﹣1<x<3时,y>0,其中正确的是( )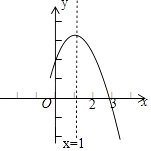 A、①②④ B、①②⑤ C、②③④ D、③④⑤
A、①②④ B、①②⑤ C、②③④ D、③④⑤二、填空题
-
6. 3的相反数是;﹣1.5的倒数是 .7. 计算:a5÷a3= .8. 分解因式: =.9. 当x=时,分式 的值为零.10. 一个圆锥的侧面积为 ,母线长为5,则此圆锥的底面半径为.11. 若m+n=1,mn=2,则的值为 .12. 任意投掷一枚均匀的骰子一次,朝上的点数不大于4的概率是.
13. 如图是二次函数 的部分图象,由图象可知不等式 的解集是.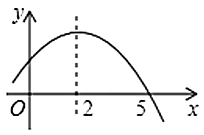 14. 如图,在菱形 中, , ,且 ,连接 交对角线 于点 ,则 .
14. 如图,在菱形 中, , ,且 ,连接 交对角线 于点 ,则 . 15. 如图, 和 分别是 的直径和弦,且 , ,交 于点 ,若 ,则 的长是.
15. 如图, 和 分别是 的直径和弦,且 , ,交 于点 ,若 ,则 的长是. 16. 如图, 中, , ,将 绕点 顺时针旋转得到 ,点 的对应点 落在边 上,已知 , ,则 的长为.
16. 如图, 中, , ,将 绕点 顺时针旋转得到 ,点 的对应点 落在边 上,已知 , ,则 的长为.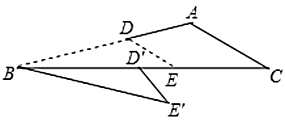
三、解答题
-
17. 计算:(1)、(2)、化简:18.(1)、解方程(2)、解不等式组:19. 某校八(1)班同学为了解2018年某小区家庭月均用水情况,随机调查了该小区部分家庭,并将调查数据进行如下整理,请解答以下问题:

 (1)、本次调查采用的调查方式是(填“普查”或“抽样调查”),样本容量是;(2)、补全频数分布直方图:(3)、若将月均用水量的频数绘成扇形统计图,则月均用水量“ ”的圆心角度数是;(4)、若该小区有5000户家庭,求该小区月均用水量超过 的家庭大约有多少户?20. 某校5月份举行了八年级生物实验考查,有A和B两个考查实验,规定每位学生只参加其中一个实验的考查,并由学生自己抽签决定具体的考查实验,小明、小丽、小华都参加了本次考查.(1)、小丽参加实验A考查的概率是;(2)、用列表或画树状图的方法求小明、小丽都参加实验A考查的概率;(3)、他们三人都参加实验A考查的概率是 .
(1)、本次调查采用的调查方式是(填“普查”或“抽样调查”),样本容量是;(2)、补全频数分布直方图:(3)、若将月均用水量的频数绘成扇形统计图,则月均用水量“ ”的圆心角度数是;(4)、若该小区有5000户家庭,求该小区月均用水量超过 的家庭大约有多少户?20. 某校5月份举行了八年级生物实验考查,有A和B两个考查实验,规定每位学生只参加其中一个实验的考查,并由学生自己抽签决定具体的考查实验,小明、小丽、小华都参加了本次考查.(1)、小丽参加实验A考查的概率是;(2)、用列表或画树状图的方法求小明、小丽都参加实验A考查的概率;(3)、他们三人都参加实验A考查的概率是 .
21. 如图,平行四边形ABCD的对角线AC、BD相交于点O, . (1)、求证: ≌ ;(2)、若 ,连接DE、BF,判断四边形EBFD的形状,并说明理由.22. 如图,一楼房 后有一假山,其坡度为 ,山坡坡面上 点处有一休息亭,测得假山坡脚 与楼房水平距离 米,与亭子距离 米,小丽从楼房顶测得 点的俯角为45°,求楼房 的高.(注:坡度 是指坡度的铅直高度与水平家度的比)
(1)、求证: ≌ ;(2)、若 ,连接DE、BF,判断四边形EBFD的形状,并说明理由.22. 如图,一楼房 后有一假山,其坡度为 ,山坡坡面上 点处有一休息亭,测得假山坡脚 与楼房水平距离 米,与亭子距离 米,小丽从楼房顶测得 点的俯角为45°,求楼房 的高.(注:坡度 是指坡度的铅直高度与水平家度的比) 23. 如图,在 中, , , , 于点 .点 从点 出发,沿线段 向点 运动,点 从点 出发,沿线段 向点 运动.两点同时出发.速度都为每秒1个单位长度,当点 运动到 时,两点都停止.设运动时间为 秒.
23. 如图,在 中, , , , 于点 .点 从点 出发,沿线段 向点 运动,点 从点 出发,沿线段 向点 运动.两点同时出发.速度都为每秒1个单位长度,当点 运动到 时,两点都停止.设运动时间为 秒. (1)、求线段 的长;(2)、设 的面积为 ,求 与 之间的函数关系式,并确定在运动过程中是否存在某一时刻 ,使得 ?若存在,求出 的值;若不存在,说明理由:24. 如图, , , 、 、 、 四点共圆,且 .
(1)、求线段 的长;(2)、设 的面积为 ,求 与 之间的函数关系式,并确定在运动过程中是否存在某一时刻 ,使得 ?若存在,求出 的值;若不存在,说明理由:24. 如图, , , 、 、 、 四点共圆,且 . (1)、确定圆的位置,圆心记为点 (要求:尺规作图,保留作图痕迹)(2)、求证: 与 相切于点 :(3)、若 , , ,求半径的长.25. 结合西昌市创建文明城市要求,某小区业主委员会决定把一块长80m,宽60m的矩形空地建成花园小广场,设计方案如图所示,阴影区域为绿化区(四块绿化区为全等的直角三角形),空白区域为活动区,且四周出口宽度一样,其宽度不小于36m,不大于44m,预计活动区造价60元/m2 , 绿化区造价50元/m2 , 设绿化区域较长直角边为xm.
(1)、确定圆的位置,圆心记为点 (要求:尺规作图,保留作图痕迹)(2)、求证: 与 相切于点 :(3)、若 , , ,求半径的长.25. 结合西昌市创建文明城市要求,某小区业主委员会决定把一块长80m,宽60m的矩形空地建成花园小广场,设计方案如图所示,阴影区域为绿化区(四块绿化区为全等的直角三角形),空白区域为活动区,且四周出口宽度一样,其宽度不小于36m,不大于44m,预计活动区造价60元/m2 , 绿化区造价50元/m2 , 设绿化区域较长直角边为xm. (1)、用含x的代数式表示出口的宽度;(2)、求工程总造价y与x的函数关系式,并直接写出x的取值范围;(3)、如果业主委员会投资28.4万元,能否完成全部工程?若能,请写出x为整数的所有工程方案;若不能,请说明理由.(4)、业主委员会决定在(3)设计的方案中,按最省钱的一种方案,先对四个绿化区域进行绿化,在实际施工中,每天比原计划多绿化11m2 , 结果提前4天完成四个区域的绿化任务,问原计划每天绿化多少m2.26. 如图①已知抛物线 的图象与 轴交于 、 两点( 在 的左侧),与 的正半轴交于点 ,连结 ;二次函数的对称轴与 轴的交点 .
(1)、用含x的代数式表示出口的宽度;(2)、求工程总造价y与x的函数关系式,并直接写出x的取值范围;(3)、如果业主委员会投资28.4万元,能否完成全部工程?若能,请写出x为整数的所有工程方案;若不能,请说明理由.(4)、业主委员会决定在(3)设计的方案中,按最省钱的一种方案,先对四个绿化区域进行绿化,在实际施工中,每天比原计划多绿化11m2 , 结果提前4天完成四个区域的绿化任务,问原计划每天绿化多少m2.26. 如图①已知抛物线 的图象与 轴交于 、 两点( 在 的左侧),与 的正半轴交于点 ,连结 ;二次函数的对称轴与 轴的交点 .
 (1)、抛物线的对称轴与 轴的交点 坐标为,点 的坐标为(2)、若以 为圆心的圆与 轴和直线 都相切,试求出抛物线的解析式:(3)、在(2)的条件下,如图② 是 的正半轴上一点,过点 作 轴的平行线,与直线 交于点 与抛物线交于点 ,连结 ,将 沿 翻折, 的对应点为 ’,在图②中探究:是否存在点 ,使得 ’恰好落在 轴上?若存在,请求出 的坐标:若不存在,请说明理由.
(1)、抛物线的对称轴与 轴的交点 坐标为,点 的坐标为(2)、若以 为圆心的圆与 轴和直线 都相切,试求出抛物线的解析式:(3)、在(2)的条件下,如图② 是 的正半轴上一点,过点 作 轴的平行线,与直线 交于点 与抛物线交于点 ,连结 ,将 沿 翻折, 的对应点为 ’,在图②中探究:是否存在点 ,使得 ’恰好落在 轴上?若存在,请求出 的坐标:若不存在,请说明理由.