江苏省盐城市盐都区、大丰区2019届九年级下学期数学期中考试试卷

试卷更新日期：2020-04-20 类型：期中考试

进入出卷网下载

一、单选题

1. $- 3$ 的倒数是（）

A、 $3$ B、 $\frac{1}{3}$ C、 $- \frac{1}{3}$ D、 $- 3$

查看试题解析
2. 下列全国各地地铁标志图中，既是轴对称图形又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 如图是由4个大小相同的小立方体搭成的几何体，它的俯视图是（）

A、 B、 C、 D、

查看试题解析
4. “厉行勤俭节约，反对铺张浪费”势在必行，最新统计数据显示，中国每年浪费食物总量折合粮食大约是210000000人一年的口粮．将210000000用科学记数法表示为（）

A、2.1×10⁹ B、0.21×10⁹ C、2.1×10⁸ D、21×10⁷

查看试题解析
5. 下列事件中，是必然事件的是（）

A、任意画一个三角形，其内角和是180° B、经过有交通信号灯的路口，遇到红灯 C、掷一次骰子，向上一面的点数是6 D、射击运动员射击一次，命中靶心

查看试题解析
6. 如图，将一块直角三角板DEF放置在锐角△ABC上，使得该三角板的两条直角边DE，DF恰好分别经过点B，C，若∠A＝50°，则∠ABD+∠ACD的值为（）

A、60° B、50° C、40° D、30°

查看试题解析
7. 关于x的一元二次方程x²+2x+3m＝0有两个不相等的实数根，则m的取值范围是（）

A、m＜ $\frac{1}{3}$ B、m≤ $\frac{1}{3}$ C、m＞﹣ $\frac{1}{2}$ D、m≤ $\frac{1}{2}$

查看试题解析
8. 如图1，在Rt△ABC中，∠ACB=90⁰ ，点P以每秒1cm的速度从点A出发，沿折线AC－CB运动，到点B停止。过点P作PD⊥AB，垂足为D，PD的长y（cm）与点P的运动时间x（秒）的函数图象如图2所示。当点P运动5秒时，PD的长是（）

A、1.5cm B、1.2cm C、1.8cm D、2cm

查看试题解析

二、填空题

9. 实数8的立方根是．

查看试题解析
10. 要使分式 $\frac{2}{1 - x}$ 有意义，则 $x$ 应满足的条件是．

查看试题解析
11. 某校在“爱护地球，绿化祖国“的创建活动中，组织了100名学生开展植数造林活动，其植树情况整理如下表：

植树棵数（单位：棵）

4

5

6

8

10

人数（人）

30

22

25

15

8

则这100名学生所植树棵数的中位数为.

查看试题解析
12. 如图，四边形ABCD为一长条形纸带，AB∥CD，将纸带ABCD沿EF折叠，A、D两点分别与A’、D’对应，若∠1＝2∠2，则∠AEF的度数为•

查看试题解析
13. 如图，O是坐标原点，菱形OABC的顶点A的坐标为 $(3 ， 4)$ ，顶点C在x轴的正半轴上，则 $∠ AOC$ 的角平分线所在直线的函数关系式为.

查看试题解析
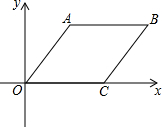14. 如图，将半径为2，圆心角为90°的扇形BAC绕点A逆时针旋转60°，点B、C的对应点分别为D、E，点D在 $\overset{⌢}{A C}$ 上，则阴影部分的面积为．

查看试题解析
15. 在平面直角坐标系中，对于点P（x，y）和Q（x，y'），给出如下定义：如果当x≥0时，y'＝y；当x＜0时，y’＝﹣y，那么称点Q为点P的“关联点“.例如：点（﹣5，6）的“关联点“为（﹣5，﹣6）.若点N（t，t﹣1）在反比例函数y＝ $\frac{2}{x}$ 的图象上，且点N是点M的“关联点”，则点M的坐标为.

查看试题解析
16. 如图，已知在Rt△ABC中，AB＝AC＝3 $\sqrt{2}$ ，在△ABC内作第1个内接正方形DEFG；然后取GF的中点P，连接PD、PE，在△PDE内作第2个内接正方形HIKJ；再取线段KJ的中点Q，在△QHI内作第3个内接正方形…，依次进行下去，则第2019个内接正方形的边长为.

查看试题解析

三、解答题

17. 计算：（3﹣π）⁰+2tan60°+|﹣2|﹣ $\sqrt{12}$ .

查看试题解析
18. 先化简，再求值： $(1 - \frac{1}{x - 1}) \div \frac{x - 2}{x^{2} - 1}$ ，其中x＝2019.

查看试题解析
19. 解不等式组 ${\begin{cases} \frac{x - 1}{2} < \frac{x}{3} \\ x + 4 \leq 3 (x + 2) \end{cases}$ ，并在数轴上表示其解集.

查看试题解析
20. 某中学开展了“手机伴我健康行”主题活动，他们随机抽取部分学生进行“使用手机目的”和“每周使用手机的时间”的问卷调查，并绘制成如图①，②所示的统计图，已知“查资料”的人数是40人.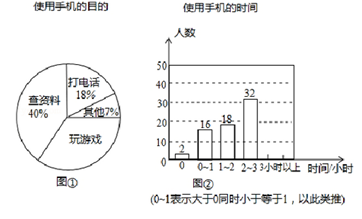

请你根据图中信息解答下列问题：

(1)、在扇形统计图中，“玩游戏”对应的圆心角度数是°；

(2)、补全条形统计图；

(3)、该校共有学生1200人，试估计每周使用手机时间在2小时以上(不含2小时)的人数.

查看试题解析
21. 某超市在端午节期间开展优惠活动，凡购物者可以通过转动转盘的方式享受折扣优惠，本次活动共有两种方式，方式一：转动转盘甲，指针指向A区域时，所购买物品享受9折优惠、指针指向其它区域无优惠；方式二：同时转动转盘甲和转盘乙，若两个转盘的指针指向每个区域的字母相同，所购买物品享受8折优惠，其它情况无优惠．在每个转盘中，指针指向每个区城的可能性相同（若指针指向分界线，则重新转动转盘）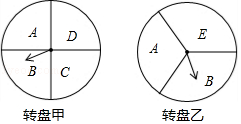

(1)、若顾客选择方式一，则享受9折优惠的概率为多少；

(2)、若顾客选择方式二，请用树状图或列表法列出所有可能，并求顾客享受8折优惠的概率．

查看试题解析
22. 如图，在平行四边形 $A B C D$ 中，过点 $D$ 作 $D E ⊥ A B$ 于点 $E$ ，点 $F$ 在边 $C D$ 上， $D F = B E$ ，连接 $A F$ ， $B F$ .

(1)、求证：四边形BFDE是矩形；

(2)、若CF=3，BE=5，AF平分∠DAB，求平行四边形 $A B C D$ 的面积.

查看试题解析
23. 已知AB是⊙O的的直径，弦CD与AB相交，∠BCD=25°。

(1)、如图1，求∠ABD的大小；

(2)、如图2，过点D作O的切线，与AB的延长线交于点P，若DP∥AC，求∠OCD的度数。

查看试题解析
24. 如图，为了将货物装入大型的集装箱卡车，需要利用传送带AB将货物从地面传送到高1.8米（即BD=1.8米）的操作平台BC上.已知传送带AB与地面所成斜坡的坡角∠BAD=37°.

(1)、求传送带AB的长度；

(2)、因实际需要，现在操作平台和传送带进行改造，如图中虚线所示，操作平台加高0.2米（即BF=0.2米），传送带与地面所成斜坡的坡度i=1：2.求改造后传送带EF的长度.（精确到0.1米）（参考数值：sin37°≈0.60，cos37°≈0.80，tan37°≈0.75， $\sqrt{2}$ ≈1.41， $\sqrt{5}$ ≈2.24）

查看试题解析
25.

(1)、问题发现

如图1，在△ABC和△ADE中，AB＝AC，AD＝AE，∠BAC＝∠DAE＝50°，连接BD，CE交于点F.填空：

①的值为；②∠BFC的度数为.

(2)、类比探究
如图2，在矩形ABCD和△DEF中，AD＝ $\sqrt{3}$ AB，∠EDF＝90°，∠DEF＝60°，连接AF交CE的延长线于点P.求 $\frac{AF}{CE}$ 的值及∠APC的度数，并说明理由；

(3)、拓展延伸
在（2）的条件下，将△DEF绕点D在平面内旋装，AF，CE所在直线交于点P，若DF＝ $\sqrt{3}$ ，AB＝ $\sqrt{7}$ ，求出当点P与点E重合时AF的长.

查看试题解析
26. 在平面直角坐标系中，已知抛物线的顶点为A（﹣1，4），且经过点B（﹣2，3），与x轴分別交于C、D两点（点C在点D的左侧）.

(1)、求该抛物线对应的函数表达式；

(2)、如图1，点M是抛物线上的一个动点，且在直线OB的上方，过点M作x轴的平行线与直线OB交于点N，连接OM.
①求MN的最大值；

②当△OMN为直角三角形时，直接写出点M的坐标；

(3)、如图2，过点A的直线交x轴于点E，且AE∥y轴，点P是抛物线上A、D之间的一个动点，直线PC、PD与AE分別交于F、G两点.当点P运动时，EF+EG的和是否为定值？若是，试求出该定值；若不是，请说明理由.

查看试题解析

植树棵数（单位：棵）	4	5	6	8	10
人数（人）	30	22	25	15	8