江苏省盐城市建湖县2019届九年级下学期数学期中考试试卷
试卷更新日期:2020-04-20 类型:期中考试
一、单选题
-
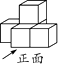
1. ﹣4的绝对值是( )A、4 B、 C、﹣4 D、±42. 下列计算中正确的是( )A、2a+3a=5a B、a3·a2=a6 C、(a-b)2=a2+b2 D、(-a2)3=-a53. 如图是由五个相同的小正方块搭成的几何体,其左视图是( )
 A、
A、 B、
B、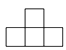 C、
C、 D、
D、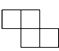 4. 下列事件是随机事件的是( )A、2019大洋湾盐城马拉松于4月21日上午在盐城市城南体育中心开赛 B、两个直角三角形相似 C、正八边形的每个外角的度数等于 D、在只装了黄球的盒子中,摸出红色的球5. 已知直线l1∥l2 , 一块含30°角的直角三角板如图所示放置,∠1=15°,则∠2等于( )
4. 下列事件是随机事件的是( )A、2019大洋湾盐城马拉松于4月21日上午在盐城市城南体育中心开赛 B、两个直角三角形相似 C、正八边形的每个外角的度数等于 D、在只装了黄球的盒子中,摸出红色的球5. 已知直线l1∥l2 , 一块含30°角的直角三角板如图所示放置,∠1=15°,则∠2等于( )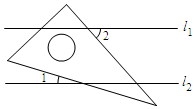 A、 B、 C、 D、6. 如图,点A,B,C在半径为9的⊙O上,OA∥BC,∠OAB=70°,则弧AC的长为( )
A、 B、 C、 D、6. 如图,点A,B,C在半径为9的⊙O上,OA∥BC,∠OAB=70°,则弧AC的长为( )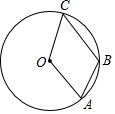 A、 B、 C、 D、7. 如图,在正方形ABCD中,G为CD的中点,连结AG并延长,交BC边的延长线于点E,对角线BD交AG于点F,已知AE=12,则线段FG的长是( )
A、 B、 C、 D、7. 如图,在正方形ABCD中,G为CD的中点,连结AG并延长,交BC边的延长线于点E,对角线BD交AG于点F,已知AE=12,则线段FG的长是( )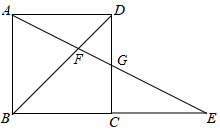 A、2 B、4 C、5 D、68. 如图,抛物线y=ax2+bx+c与x轴交于A,B两点,与y轴交于C点,DE是正三角形ABC的中位线.动点M,N分别从D、E出发,沿着射线DE与射线EB方向移动相同的路程,连结AM,DN交于P点.则下列结论:①ac=-3;②AM=DN;③无论M,N处何位置,∠APN的大小始终不变.其中正确的是( )
A、2 B、4 C、5 D、68. 如图,抛物线y=ax2+bx+c与x轴交于A,B两点,与y轴交于C点,DE是正三角形ABC的中位线.动点M,N分别从D、E出发,沿着射线DE与射线EB方向移动相同的路程,连结AM,DN交于P点.则下列结论:①ac=-3;②AM=DN;③无论M,N处何位置,∠APN的大小始终不变.其中正确的是( )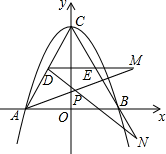 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
9. 若分式 有意义,则x满足.10. 因式分解:-2x2+12x-18=.11. 随着人们对环境的重视,新能源的开发迫在眉睫,石墨烯使现在世界上最薄的纳米材料,其理论厚度应是0.00000000034m,用科学记数法表示是 .
12. 已知组数据4,x,6,y,9,12的平均数为7,众数为6,则这组数据的方差为.13. 如图,▱ABCD中,对角线AC、BD交于点O,OE⊥DB,垂足为点O,交DC于点E,若△BEC的周长为6,则▱ABCD的周长等于. 14. 如图,在平面直角坐标系中,直线y=3x+3与x轴、y轴分别交于A、B两点,以线段AB为边在第二象限内作正方形ABCD,点C恰好落在双曲线y= 上,则k的值是.
14. 如图,在平面直角坐标系中,直线y=3x+3与x轴、y轴分别交于A、B两点,以线段AB为边在第二象限内作正方形ABCD,点C恰好落在双曲线y= 上,则k的值是.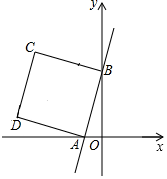 15. 在如图的正方形方格纸中,每个小的四边形都是相同的正方形,A,B,C,D都在格点处,AB与CD相交于O,则tan∠BOD的值等于 .
15. 在如图的正方形方格纸中,每个小的四边形都是相同的正方形,A,B,C,D都在格点处,AB与CD相交于O,则tan∠BOD的值等于 .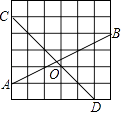 16. 如图,已知AB=12,P为线段AB上的一个动点,分别以AP、PB为边在AB的同侧作菱形APCD和菱形PBFE,点P、C、E在一条直线上,∠DAP=60°.M、N分别是对角线AC、BE的中点.当点P在线段AB上移动时,点M、N之间的距离最短为.(结果留根号)
16. 如图,已知AB=12,P为线段AB上的一个动点,分别以AP、PB为边在AB的同侧作菱形APCD和菱形PBFE,点P、C、E在一条直线上,∠DAP=60°.M、N分别是对角线AC、BE的中点.当点P在线段AB上移动时,点M、N之间的距离最短为.(结果留根号)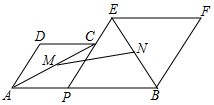
三、解答题
-
17. 计算:(2019-π)0+ +sin245°+(- -2.18. 求不等式组 的正整数解.19. 先化简,再求值: ,其中x为方程 的根.20. 校园手机现象已经受到社会的广泛关注.某校的一个兴趣小组对“是否赞成中学生带手机进校园”的问题在该校校园内进行了随机调查.并将调查数据作出如下不完整的整理;
看法
频数
频率
赞成
5
无所谓
0.1
反对
40
0.8
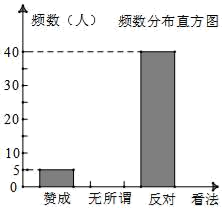 (1)、本次调查共调查了人;(直接填空)(2)、请把整理的不完整图表补充完整;(3)、若该校有3000名学生,请您估计该校持“反对”态度的学生人数.21. 在一个不透明的口袋里装有分别标有数字-3、-1、0、2的四个小球,除数字不同外,小球没有任何区别,每次试验先搅拌均匀.(1)、从中任取一球,将球上的数字记为a,则关于x的元二次方程x2-2x-a+1=0有实数根的概率;(2)、从中任取一球,将球上的数字作为点的横坐标,记为x(不放回);再任取一球,将球上的数字作为点的纵坐标,记为y,试用画树状图(或列表法)表示出点(x,y)所有可能出现的结果,并求点(x,y)落在第三象限内的概率.22. 如图,在△ABC中,∠BAC=90°.
(1)、本次调查共调查了人;(直接填空)(2)、请把整理的不完整图表补充完整;(3)、若该校有3000名学生,请您估计该校持“反对”态度的学生人数.21. 在一个不透明的口袋里装有分别标有数字-3、-1、0、2的四个小球,除数字不同外,小球没有任何区别,每次试验先搅拌均匀.(1)、从中任取一球,将球上的数字记为a,则关于x的元二次方程x2-2x-a+1=0有实数根的概率;(2)、从中任取一球,将球上的数字作为点的横坐标,记为x(不放回);再任取一球,将球上的数字作为点的纵坐标,记为y,试用画树状图(或列表法)表示出点(x,y)所有可能出现的结果,并求点(x,y)落在第三象限内的概率.22. 如图,在△ABC中,∠BAC=90°.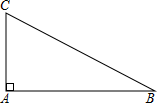 (1)、利用直尺和圆规按下列要求作图,并在图中标明相应的字母(保留作图痕迹,不写作法).
(1)、利用直尺和圆规按下列要求作图,并在图中标明相应的字母(保留作图痕迹,不写作法).①作BC的垂直平分线EF,交AB、BC,分别于点E、F;
②在射线EF上取一点D(异于点E),使∠DBC=∠EBC;
③连接CE、CD、BD.
(2)、判定四边形CEBD的形状,并说明你的理由;(3)、若AC=5,AB=12,求EF的长.23. 如图,点D为⊙O上一点,点C在直径AB的延长线上,且∠COD=2∠BDC,过点A作⊙O的切线,交CD的延长线于点E.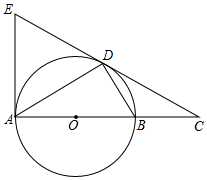 (1)、判定直线CD与⊙O的位置关系,并说明你的理由;(2)、若CB=4,CD=8,求ED的长.24. 金桥学校“科技体艺节”期间,八年级数学活动小组的任务是测量学校旗杆AB的高.他们在旗杆正前方台阶上的点C处,测得旗杆顶端A的仰角为45°,朝着旗杆的方向走到台阶下的点F处,测得旗杆顶端
(1)、判定直线CD与⊙O的位置关系,并说明你的理由;(2)、若CB=4,CD=8,求ED的长.24. 金桥学校“科技体艺节”期间,八年级数学活动小组的任务是测量学校旗杆AB的高.他们在旗杆正前方台阶上的点C处,测得旗杆顶端A的仰角为45°,朝着旗杆的方向走到台阶下的点F处,测得旗杆顶端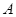 的仰角为60°.已知升旗台的高度BE为1米,点
的仰角为60°.已知升旗台的高度BE为1米,点 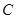 距地面的高度CD为3米,台阶CF的坡角为30°,且点E,F,D在同一条直线上.求旗杆AB的高.(计算结果精确到0.1米,参考数据: )
距地面的高度CD为3米,台阶CF的坡角为30°,且点E,F,D在同一条直线上.求旗杆AB的高.(计算结果精确到0.1米,参考数据: )  25. 文美书店决定用不多于20000元购进甲乙两种图书共1200本进行销售.甲、乙两种图书的进价分别为每本20元、14元,甲种图书每本的售价是乙种图书每本售价的1.4倍,若用1680元在文美书店可购买甲种图书的本数比用1400元购买乙种图书的本数少10本.
25. 文美书店决定用不多于20000元购进甲乙两种图书共1200本进行销售.甲、乙两种图书的进价分别为每本20元、14元,甲种图书每本的售价是乙种图书每本售价的1.4倍,若用1680元在文美书店可购买甲种图书的本数比用1400元购买乙种图书的本数少10本.
(1)、甲乙两种图书的售价分别为每本多少元?(2)、书店为了让利读者,决定甲种图书售价每本降低3元,乙种图书售价每本降低2元,问书店应如何进货才能获得最大利润?(购进的两种图书全部销售完.)
26. 已知,在△ABC中,以△ABC的两边BC,AC为斜边向外测作Rt△BCD和Rt△ACE,使∠CAE=∠CBD,取△ABC边AB的中点M,连接ME,MD.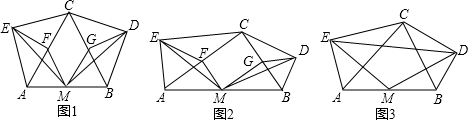
特例感知:
(1)、如图1,若AC=BC,∠ACB=60°,∠CAE=∠CBD=45°,取AC,BC的中点F,G,连接MF,MG,EF,DG,则ME与MD的数量关系为 , ∠EMD=;(2)、如图2,若∠ACB=90°,∠CAE=∠CBD=60°,取AC,BC的中点F,G,连接MF,MG,EF,DG,请猜想ME与MD的数量关系以及∠EMD的度数,并给出证明;类比探究:
(3)、如图3,当△ABC是任意三角形,∠CAE=∠CBD=α时,连接DE,请猜想△DEM的形状以及∠EMD与α的数量关系,并说明理由.27. 如图,抛物线y=ax2+4x+c与x轴交于A、B两点,交y轴交于点C,直线y=-x+5经过点B、C.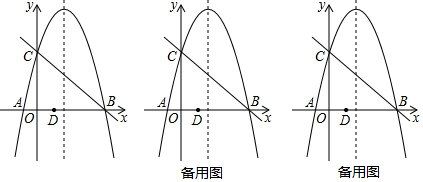 (1)、求抛物线的表达式;(2)、点D(1,0),点P为对称轴上一动点,连接BP、CP.
(1)、求抛物线的表达式;(2)、点D(1,0),点P为对称轴上一动点,连接BP、CP.①若∠CPB=90°,求点P的坐标;
②点Q为抛物线上一动点,若以C、D、P、Q为顶点的四边形是平行四边形,求P的坐标.