甘肃省庆阳市镇原县2019届九年级下学期数学期中考试试卷
试卷更新日期：2020-04-20 类型：期中考试
一、单选题
-
1. 四个实数0， ，﹣3.14，π，最大的数是（ ）A、0 B、 C、﹣3.14 D、π2. 如图是某几何体的三视图，则该几何体是（ ）
A、圆锥 B、圆柱 C、三棱柱 D、三棱锥3. 2018年10月23日，港珠澳大桥开通，港珠澳大桥东起香港国际机场附近的香港口岸人工岛，向西横跨伶仃洋海域后连按珠海和澳门人工岛，止于珠海祺湾，工程项目总投资额1269亿元，数据1269亿元用科学记数法可表示为（ ）A、1269×108元 B、126.9×109元 C、1.269×1011元 D、1.269×108元4. 下列计算中，正确的是（ ）A、a2•a3＝a5 B、（a2）3＝a8 C、a3+a2＝a5 D、a8÷a4＝a25. 平面直角坐标系中点A、B的坐标分别为（0，4）和（3，2），在x轴上确定一点C，使点C到点A、B的距离之和最小，则点C的坐标为（ ）A、（﹣2，0） B、（2，0） C、（﹣6，0） D、（6，0）6. 若一组数据1，3，x，5，8的众数为8，则这组数据的中位数为（ ）A、1 B、3 C、5 D、87. 的近似值在（ ）A、1和2之间 B、2和3之间 C、3和4之间 D、4和5之间8. 程大位是我国明朝商人，珠算发明家．他60岁时完成的《直指算法统宗》是东方古代数学名著，详述了传统的珠算规则，确立了算盘用法．书中有如下问题：一百馒头一百僧，大僧三个更无争，小僧三人分一个，大小和尚得几丁．意思是：有100个和尚分100个馒头，如果大和尚1人分3个，小和尚3人分1个，正好分完，大、小和尚各有多少人，下列求解结果正确的是（ ）
A、大和尚25人，小和尚75人 B、大和尚75人，小和尚25人 C、大和尚50人，小和尚50人 D、大、小和尚各100人9. 如图，直线AB是⊙O的切线，点C为切点，OD∥AB交⊙O于点D，点E在⊙O上，连接OC，EC，ED，则∠CED的度数为（ ）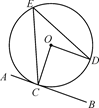
A、30° B、35° C、40° D、45°10. 如图，在任意四边形ABCD中，AC，BD是对角线，E，F，G，H分别是线段BD，BC，AC，AD上的点，对于四边形EFGH的形状，某班的学生在一次数学活动课中，通过动手实践，探索出如下结论，其中错误的是（ ）
A、当E，F，G，H是各条线段的中点时，四边形EFGH为平行四边形 B、当E，F，G，H是各条线段的中点，且AC⊥BD时，四边形EFGH为矩形 C、当E，F，G，H是各条线段的中点，且AB=CD时，四边形EFGH为菱形 D、当E，F，G，H不是各条线段的中点时，四边形EFGH可以为平行四边形二、填空题
-
11. 计算： ＝.12. △ABC中，BC＝8，AB，AC的中点分别为D，E，则DE＝.13. 不等式组 的解集为 ．14. 若α、β是一元二次方程x2+2x﹣3＝0的两个不相等的根，则α2﹣2β的值是.15. 如图，这是生活中经常接触的小刀，刀片的外壳是四边形，而且刀片外壳与刀片合部分都是直角，刀片的上，下是平行的动刀片时会形成∠1和∠2，则∠1+∠2＝.
16. 在直角三角形ABC中，∠ACB=90°，D、E是边AB上两点，且CE所在直线垂直平分线段AD，CD平分∠BCE，BC=2 ，则AB=.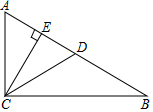
17. 如图，直线 与 轴、 轴分别交于A，B两点，C是OB的中点，D是AB上一点，四边形OEDC是菱形，则△OAE的面积为 ．
18. 观察下列等式：21＝2，22＝4，23＝8，24＝16，25＝32，26＝64，…，根据这个规律，则21+22+23+…+22019的末尾数字是.三、解答题
-
19. 化简： .20. 如图，已知等腰△ABC，在底边BC上任取一点P，作PN⊥AC于N，BD⊥AC于D.
(1)、用尺规作出PM⊥AB于M，不写作法，保留作图痕迹；(2)、求证：PM+PN＝BD.21. 多肉植物因体积小、外形萌、色彩斑斓，茶几阳台摆放方便，深爱养花爱好者的喜欢，某花店抓住这个商机，第一次购进甲、乙两种多肉植物共300株.甲种多肉植物每株成本4元，售价8元；乙种多肉植物每株成本6元，售价10元.若第一次购进多肉植物的金额为1400元，则甲种多肉植物购进多少株？
22. 如图，育英学校前方有一斜坡AB长60米，坡度i＝1： ，BC⊥AC，现计划在斜坡中点D处挖去部分坡体（用阴影表示），修建一个平行于水平线CA的平台DE和一条新的斜坡BE.
(1)、若修建的斜坡BE的坡角（即∠BEF）不大于45°，则平合DE最长是多少米？(2)、学校教学楼GH距离坡脚A点27米远（即AG＝27米），小明在D点测得教学楼顶部H的仰角（即∠HDM）为30°.点B、C、A、G、H在同一个平面上，点C、A、G在同一条直线上，且HG⊥CG，问：教学楼GH高为多少米？（结果精确到0.1米，参考数据 ≈1.732）23. 为弘扬“东亚文化”，某单位开展了“东亚文化之都”演讲比赛，在安排1位女选手和3位男选手的出场顺序时，采用随机抽签方式．(1)、请直接写出第一位出场是女选手的概率；(2)、请你用画树状图或列表的方法表示第一、二位出场选手的所有等可能结果，并求出他们都是男选手的概率．24. 某校为了解七年级学生最喜欢的校本课程（厨艺课数字与生活、足球、采花戏）情况，随机抽取了七年级部分学生进行问卷调查，每名同学选且只选一门现将调查结果绘制成如下所示的两幅统计图：
请结合这两幅统计图，解决下列问题：
(1)、在这次问卷调查中，一共抽取了名学生；(2)、请补全条形统计图；(3)、若该校七年级共有1050名学生，请你估计其中最喜欢数字与生活的学生人数.25. 如图，一次函数y＝kx+b的图象与反比例函数y＝ 的图象交于点P（2，6），过点P作PA⊥x轴于A，PB⊥y轴于点B.一次函数的图象分别交x轴、y轴于点C、D，若tan∠DCO＝2.
(1)、求一次函数与反比例函数的解析式；(2)、求△BDP的面积，并根据图象写出当x＞0时，一次函数的值大于反比例函数的值的x的取值范围.26. 如图，矩形ABCD中，AC＝4，AB＝2，将矩形ABCD绕点A旋转得到矩形AB'C'D'，使点B的对应点B'落在AC上，B'C'交AD于点E，在B'C'上取点F，使B'F＝AB.
(1)、求证：AE＝C'E；(2)、求BF的长.27. 如图，在Rt△ABC中，∠C=90°，BE平分∠ABC交AC于点E，作ED⊥EB交AB于点D，⊙O是△BED的外接圆.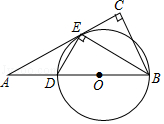
(1)、求证：AC是⊙O的切线；(2)、已知⊙O的半径为2.5，BE=4，求BC，AD的长.28. 如图，已知抛物线y＝mx2﹣4mx+3m（m＞0）与x轴的交点为A，B，与y轴的交点为C，D为抛物线的顶点.
(1)、直接写出各点坐标C（ ， ），D（ ， ）；（用m表示）(2)、试说明无论m为何值，抛物线一定经过两个定点并求出这两个定点的坐标；(3)、①将线段AC绕点A顺时针旋转90°得到AC′，求点C′的坐标；②连接DC'，AD，是否存在m，使得△ADC′为等腰三角形？若存在，请求出m；若不存在，请说明理由.