甘肃省定西市临洮县2019届九年级下学期数学期中考试试卷

试卷更新日期：2020-04-20 类型：期中考试

进入出卷网下载

一、单选题

1. ﹣3的绝对值是（）

A、﹣3 B、3 C、- $\frac{1}{3}$ D、 $\frac{1}{3}$

查看试题解析
2. 十九大报告指出，我国目前经济保持了中高速增长，在世界主要国家中名列前茅，国内生产总值从54万亿元增长80万亿元，稳居世界第二，其中80万亿用科学记数法表示为（）

A、8×10¹² B、8×10¹³ C、8×10¹⁴ D、0.8×10¹³

查看试题解析
3. 下列计算正确的是（）

A、4a﹣2a＝2 B、2x²+2x²＝4x⁴ C、﹣2x²y﹣3yx²＝﹣5x²y D、2a²b﹣3a²b＝a²b

查看试题解析
4. 下列图形中，不是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
5. 如图，直线a∥b，CD⊥AB于点D，若∠1＝36°，则∠2等于（）

A、54° B、126° C、136° D、144°

查看试题解析
6. 下列二次根式中是最简二次根式的是（）

A、 $\sqrt{6}$ B、 $\sqrt{18}$ C、 $\sqrt{27}$ D、 $\sqrt{12}$

查看试题解析
7. 计算 $\frac{3 x}{x - 1} - \frac{3}{x-1}$ 的结果是（）

A、 $\frac{x}{x-1}$ B、x C、3 D、0

查看试题解析
8. 如图，矩形 $A B C D$ 中，对角线 $A C 、 B D$ 交于点 $O$ .若 $∠ A O B = 60^{\circ} ， B D = 8$ ，则 $A B$ 的长为（）

A、 $3$ B、 $4$ C、 $4 \sqrt{3}$ D、 $5$

查看试题解析
9. 如图，在△ABC中，点D，E分别在边AB，AC上，且DE∥BC， $\frac{A D}{B D} ＝ \frac{1}{2}$ ，若S_△_ADE＝2，则S_△_ABC的值是（）

A、6 B、8 C、18 D、32

查看试题解析
10. 已知抛物线y＝ax²＋bx＋c（a≠0）的对称轴为直线x＝2，与x轴的一个交点坐标为（4，0），其部分图象如图所示，下列结论正确的是（）

A、当x＜2时，y随x增大而增大 B、a－b＋c＜0 C、拋物线过点（－4，0） D、4a＋b＝0

查看试题解析

二、填空题

11. 分解因式：a²b−8ab+16b=.

查看试题解析
12. 如图，在△ABC中，AB＝BC，∠ABC＝120°，AB的垂直平分线DE交AC于点D，连接BD，则∠ABD＝°.

查看试题解析
13. 如图，AB是⊙O的直径，点C和点D在⊙O上，若∠BDC＝20°，则∠AOC等于度.

查看试题解析
14. 若 $x = 1$ 是一元二次方程 $x^{2} + 3 x + m = 0$ 的一个根，则 $m =$ .

查看试题解析
15. 如图，直线y=3x和y=kx+2相交于点P（a，3），则不等式3x≥kx+2的解集为.

查看试题解析
16. 如图，在Rt△ABC中，∠B＝90°，AB＝2，以B为圆心，AB为半径画弧，恰好经过AC的中点D，则弧AD与线段AD围成的弓形面积是.

查看试题解析
17. 符号“f”表示一种运算，它对一些数的运算结果如下：
f（1）＝0；f（2）＝1；f（3）＝2；f（4）＝3；

f（ $\frac{1}{2}$ ）＝3；f（ $\frac{1}{3}$ ）＝4；f（ $\frac{1}{4}$ ）＝5；f（ $\frac{1}{5}$ ）＝6；

利用以上规律计算：f（ $\frac{1}{2019}$ ）－f（2019）＝.

查看试题解析

三、解答题

18. 解不等式组.
${\begin{array}{l} x ＋ 1 \leq 2 \\ \frac{1 ＋ 2 x}{3} > x － 1 \end{array}$

查看试题解析
19. 如图，在△ABC中，∠B=40°，∠C=80°，按要求完成下列各题：

(1)、作△ABC的角平分线AE；

(2)、根据你所画的图形求∠BAE的度数.

查看试题解析
20. 我国民间流传着许多趣味算题，它们多以顺口溜的形式表达，其中《孙子算经》中记载了这样一个数学问题：一群老头去赶集，半路买了一堆梨，一人一个多一梨，一人两个少二梨，请问君子知道否，几个老头几个梨？

查看试题解析
21. 小明家所在居民楼的对面有一座大厦AB＝74米，为测量这座居民楼与大厦之间的水平距离CD的长度，小明从自己家的窗户C处测得∠DCA＝37°，∠DCB＝48°(DC平行于地面).求小明家所在居民楼与大厦的距离CD的长度.
（参考数据：sin37° $\approx \frac{3}{5}$ ，tan37° $\approx \frac{3}{4}$ ，sin48° $\approx \frac{7}{10}$ ，tan48° $\approx \frac{11}{10}$ ）

查看试题解析
22. 随着信息技术的迅猛发展，人们去商场购物的支付方式更加多样、便捷，在一次购物中，张华和李红都想从“微信”、“支付宝”、“银行卡”、“现金”四种支付方式中选一种方式进行支付.

(1)、张华用“微信”支付的概率是.

(2)、请用画树状图或列表法求出两人恰好选择同一种支付方式的概率.(其中“微信”、“支付宝”、“银行卡”、“现金”分别用字母“A”“B”“C”“D”代替)

查看试题解析

23. 小明同学以“你最喜欢的运动项目”为主题，对公园里参加运动的群众进行随机调查（每名被调查者只能选一个项目，且被调查者都进行了选择）.下面是小明根据调查结果列出的统计表和绘制的扇形统计图（不完整）.

被调查者男、女所选项目人数统计表

项目	男（人数）	女（人数）
广场舞	7	9
健步走	$m$	4
器械	2	2
跑步	5	$n$

根据以上信息回答下列问题：

(1)、统计表中的

m =

，

n =

(2)、扇形统计图中“广场舞”项目所对应扇形的圆心角度数为°.

(3)、若平均每天来该公园运动的人数有3600人，请你估计这3600人中最喜欢的运动项目是“跑步”的约有多少人？

查看试题解析

24. 如图，线段OA与反比例函数y $＝ \frac{m － 1}{x}$ 在第一象限的图象相交于点B（4，3），点B是OA的中点，AC∥x轴交反比例函数的图象于点C.

求：

(1)、m的值；

(2)、求AC的长.

查看试题解析
25. 如图，点A，B，C，D在同一条直线上，点E，F分别在直线AD的两侧，且AE＝DF，∠A＝∠D，AB＝DC.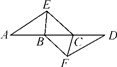

(1)、求证：△AEC≌△DFB；

(2)、若∠EBD＝60°，BE＝BC，求证：四边形BFCE是菱形.

查看试题解析
26. 如图，已知AB为⊙O的直径，AB⊥AC，BC交⊙O于D，E是AC的中点，AD＝2BD，ED与AB的延长线相交于点F，连接AD.

(1)、求证：DE为⊙O的切线.

(2)、求证：△FDB∽△FAD；

(3)、若BF＝2，求⊙O的半径.

查看试题解析
27. 如图1，抛物线y＝﹣x²+mx+n交x轴于点A(﹣2，0)和点B，交y轴于点C(0，2).

(1)、求抛物线的函数表达式；

(2)、若点M在抛物线上，且S_△_AOM＝2S_△_BOC ，求点M的坐标；

(3)、如图2，设点N是线段AC上的一动点，作DN⊥x轴，交抛物线于点D，求线段DN长度的最大值.

查看试题解析