云南省昭通市2018-2019八年级下学期数学期中考试试卷
试卷更新日期:2020-04-20 类型:期中考试
一、单选题
-
1. 下列根式中,是最简二次根式的是( )A、 B、 C、 D、2. 若a≤1,则 化简后为( )A、 B、 C、 D、3. 已知 ,化简二次根式 的正确结果为( )A、 B、 C、 D、4. 已知一直角三角形的木板,三条边长的平方和为1800cm2 ,则斜边长为( )A、80ccm B、120cm C、90cm D、30cm5. 如果等边三角形的边长为3,那么连接各边中点所成的三角形的周长为( )A、9 B、6 C、3 D、6. △ABC中,AB=13,AC=15,高AD=12,则BC的长为( )A、14 B、4 C、14或4 D、以上都不对7. 平行四边形的两条对角线长分别为6和10,则平行四边形的一条边的长x的取值范围为( )A、4<x<6 B、2<x<8 C、0<x<10 D、0<x<68. 将一张平行四边形的纸片折一次,使得折痕平分这个平行四边形的面积.则这样的折纸方法共有( )
A、1种 B、2种 C、4种 D、无数种9. 平行四边形的周长为24cm,相邻两边长的比为3:1,那么这个平行四边形较短的边长为( )A、6cm B、3cm C、9cm D、12cm10. 如图,点 的坐标为 ,点 在直线 上运动,当线段 最短时,点 的坐标为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 当 时, 是二次根式.12. 在实数范围内分解因式: .13. 王师傅在操场上安装一副单杠,要求单杠与地面平行,杠与两撑脚垂直,如图所示,撑脚长AB,DC为3 m,两撑脚间的距离BC为4 m,则AC=m就符合要求.
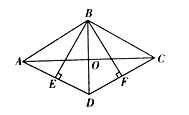
 14. 如图,在平行四边形ABCD中,DB=DC,∠C=70°,AE⊥BD于E,则∠DAE=度.
14. 如图,在平行四边形ABCD中,DB=DC,∠C=70°,AE⊥BD于E,则∠DAE=度. 15. 在 中, 的对边分别是 ,若 ,又 ,则最大边上的高为.16. 如图,在□ 中, ⊥ 于点 , ⊥ 于点 .若 , ,且□ 的周长为40,则□ 的面积为。
15. 在 中, 的对边分别是 ,若 ,又 ,则最大边上的高为.16. 如图,在□ 中, ⊥ 于点 , ⊥ 于点 .若 , ,且□ 的周长为40,则□ 的面积为。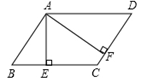 17. 已知平行四边形ABCD的两条对角线相交于直角坐标系的原点,点A,B的坐标分别为(﹣2,﹣3),(﹣1,2),则C、D的坐标分别为.18. 已知第一个三角形的周长为1,它的三条中位线组成第二个三角形,第二个三角形的三条中位线又组成第三个三角形,依此类推,第2007个三角形的周长为.
17. 已知平行四边形ABCD的两条对角线相交于直角坐标系的原点,点A,B的坐标分别为(﹣2,﹣3),(﹣1,2),则C、D的坐标分别为.18. 已知第一个三角形的周长为1,它的三条中位线组成第二个三角形,第二个三角形的三条中位线又组成第三个三角形,依此类推,第2007个三角形的周长为.三、解答题
-
19. 计算:(1)、 ;(2)、20. 已知 ,求值:(1)、(2)、21. 已知 的三边长分别为 ,求证: 是直角三角形.22. 如图,在平行四边形 中, 分别为垂足,试说明四边形 是平行四边形.
 23. 已知:如图,在平行四边形 中, 、 是对角线 上的两点,且 .
23. 已知:如图,在平行四边形 中, 、 是对角线 上的两点,且 .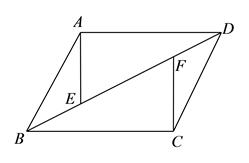
求证:
(1)、 .
(2)、 .