贵州省黔东南、黔南、黔西南2018-2019八年级下学期数学期中考试试卷
试卷更新日期：2020-04-20 类型：期中考试
一、单选题
-
1. 下列二次根式中，属于最简二次根式的是（ ）A、 B、 C、 D、2. 若二次根式 有意义，则x应满足（ ）A、x≥3 B、x≥﹣3 C、x＞3 D、x＞﹣33. 正方形面积为36，则对角线的长为（ ）A、6 B、6 C、9 D、94. 矩形的两条对角线的夹角为60°，对角线长为15cm，较短边的长为（ ）A、12cm B、10cm C、7.5cm D、5cm5. 下列命题中，正确的个数是（ ）
①若三条线段的比为1：1： ，则它们组成一个等腰直角三角形；②两条对角线相等的平行四边形是矩形；③对角线互相垂直的四边形是菱形；④有两个角相等的梯形是等腰梯形；⑤一条直线与矩形的一组对边相交，必分矩形为两个直角梯形。
A、2个 B、3个 C、4个 D、5个6. 能判定四边形是平行四边形的是（ ）A、对角线互相垂直 B、对角线相等 C、对角线互相垂直且相等 D、对角线互相平分7. 如图，在▱ABCD中，已知AD=5cm，AB=3cm，AE平分∠BAD交BC边于点E，则EC等于（ ）
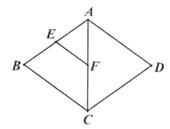
A、1cm B、2cm C、3cm D、4cm8.如图，菱形ABCD中，E、F分别是AB、AC的中点，若EF=3，则菱形ABCD的周长是（ ）
A、12 B、16 C、20 D、249. 如图，在矩形 中， ，将矩形沿对角线 折叠，则重叠部分 的面积为（ ）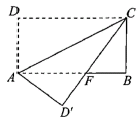
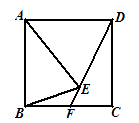
A、12 B、10 C、8 D、610.如图，正方形ABCD中，AE＝AB，直线DE交BC于点F，则∠BEF＝（ ）
A、45° B、30° C、60° D、55°二、填空题
-
11. 已知 中一条对角线分 为35°和45°，则 度.12. 矩形的两条对角线的夹角为 ，较短的边长为 ，则对角线长为 .13. 小强想知道学校旗杆的高度，他发现旗杆上的绳子垂到地面上还多1米，当他把绳子的下端拉开5米后，发现下端刚好接触地面，则旗杆的高度是米.
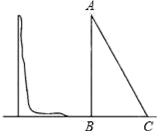14. 已知菱形的两条对角线长为8cm和6cm，那么这个菱形的周长是cm，面积是cm2.15. 在平面直角坐标系中，点A（﹣1，0）与点B（0，2）的距离是16. 如图，每个小正方形的边长为1，在△ABC中，点D为AB的中点，则线段CD的长为.
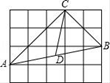17. 如图，AD是△ABC的角平分线，DE∥AC交AB于E，DF∥AB交AC于F．且AD交EF于O，则∠AOF＝度．
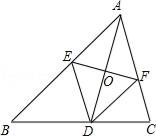18. 若AD＝8，AB＝4，那么当BC＝ ， CD＝时，四边形ABCD是平行四边形.19. 若AC＝10，BD＝8，那么当AO＝DO＝时，四边形ABCD是平行四边形。20. 观察下列各式： =2 ； =3 ； =4 ，……请你将发现的规律用含自然数n（n≥1）的等式表示出来 ．三、解答题
-
21. 计算题：(1)、(2)、(3)、(4)、3 .22. 如图，已知▱ABCD中，AE平分∠BAD，CF平分∠BCD，分别交BC、AD于E、F.求证：AF＝EC.
23. 已知：如图，四边形ABCD四条边上的中点分别为E、F、G、H，顺次连接EF、FG、GH、HE，得到四边形EFGH（即四边形ABCD的中点四边形）．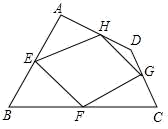
(1)、四边形EFGH的形状是 ， 证明你的结论；(2)、当四边形ABCD的对角线满足条件时，四边形EFGH是矩形；(3)、你学过的哪种特殊四边形的中点四边形是矩形？ ． （不证明）24. 如图，▱ABCD的对角线AC、BD相交于点O，E、F是AC上的两点，并且AE＝CF，求证：四边形BFDE是平行四边形．
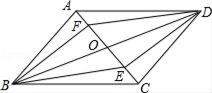25. 如图在△ABC中， ACB=90°，点D，E分别是AC、AB的中点，点F在BC的延长线上，且 CDF= A．求证：四边形DECF是平行四边形.
