甘肃省张掖市临泽二中、三中、四中2018-2019八年级下学期数学期中考试试卷

试卷更新日期：2020-04-20 类型：期中考试

进入出卷网下载

一、单选题

1. 下列学生喜欢的手机应用软件图标中，是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 若不等式组 ${\begin{matrix} x \geq a \\ x < b \end{matrix}$ 无解，则有（）

A、b＞a B、b＜a C、b=a D、b≤a

查看试题解析
3.
已知，如图，在△ABC中，OB和OC分别平分∠ABC和∠ACB，过O作DE∥BC，分别交AB、AC于点D、E，若BD+CE=5，则线段DE的长为（　　）

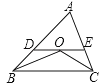A、5 B、6 C、7 D、8

查看试题解析
4. 若不等式ax+x＞1+a的解集是x＜1，则a必须满足的条件是（）

A、 $a < - 1$ B、 $a < 1$ C、 $a > - 1$ D、 $a > 1$

查看试题解析
5.
如图，两个直角三角形重叠在一起，将其中一个三角形沿着BC边平移到△DEF的位置，∠B=90°，AB=10，DH=2，平移距离为3，则阴影部分的面积为（　　）

A、20 B、24 C、27 D、36

查看试题解析
6. 在方程组 ${\begin{array}{l} 2 x + y = 1 - m \\ x + 2 y = 2 \end{array}$ 中，若未知数x，y满足x+y＞0，则m的取值范围在数轴上的表示应是如图所示的（）

A、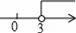 B、 C、 D、

查看试题解析
7. 在平面直角坐标系中，点P（﹣1，2）向上平移3个单位长度后的坐标是（）

A、（2，2） B、（﹣4，2） C、（﹣1，5） D、（﹣1，﹣1）

查看试题解析
8. 如图，在等边三角形ABC中，AB=6，D是BC上一点，且BC=3BD，△ABD绕点A旋转后得到△ACE，则CE的长度为（）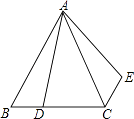

A、6 B、5 C、3 D、2

查看试题解析
9. 已知等腰三角形的一边长5cm，另一边长8cm，则它的周长是（）

A、18cm B、21cm C、18cm或21cm D、无法确定

查看试题解析
10. 已知在△ABC中，AB＝AC，AB的垂直平分线交线段AC于D，若△ABC和△DBC的周长分别是60 cm和38 cm，则△ABC的腰长和底边BC的长分别是（）

A、22cm和16cm B、16cm和22cm C、20cm和16cm D、24cm和12cm

查看试题解析

二、填空题

11. 已知三角形的两边为3和4，则第三边a的取值范围是.

查看试题解析
12. 如图所示，在△ABC中，∠B=90°，AB=3，AC=5，将△ABC折叠，使点C与点A重合，折痕为DE，则△ABE的周长为.

查看试题解析
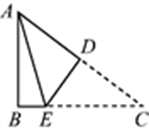13. 等腰三角形的底角为15°，腰长为3a，则等腰三角形腰上的高是.

查看试题解析
14. 若关于x的不等式（1﹣a）x＞2可化为x＞ $\frac{2}{1 - a}$ ，则a的取值范围是．

查看试题解析
15. 如图，△ABC中，DE垂直平分BC，垂足为E，交AB于D，若AB=10 cm，AC=6 cm，则△ACD的周长为cm.

查看试题解析
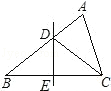16. 如图，一次函数y＝kx+b（k≠0）的图象如图所示，则关于x的不等式kx+b＞2的解集应是.

查看试题解析
17. 若不等式组 ${\begin{array}{l} 2 x + 10 < 5 x - 2 \\ 3 x > 2 m + 1 \end{array}$ 的解集是x＞4，则m的取值范围是.

查看试题解析
18. 如图，长方形ABCD中，BC=6，CD=3，将△BCD沿对角线BD翻折，点C落在点C’处，BC’交AD于点E，则线段DE的长为.

查看试题解析

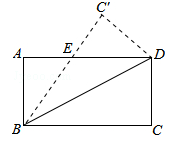
三、解答题

19.

(1)、解不等式，并把解集在数轴上表示出来： $\frac{x - 1}{2} < \frac{4 x - 5}{3}$

(2)、解不等式组： ${\begin{array}{l} 5 x - 6 \leq 2 (x + 3) \\ \frac{x}{4} - 1 < \frac{x - 3}{3} \end{array}$ 并写出它的所有的整数解.

查看试题解析
20. 已知方程组 ${\begin{array}{l} x - y = 2 k \\ x + 3 y = 1 - 5 k \end{array}$ 的解x与y的和为负数，求k的取值范围.

查看试题解析
21. 如图，在△ABC中，AC=BC，∠C=90°，AD是△ABC的角平分线，DE⊥AB，垂足为E.

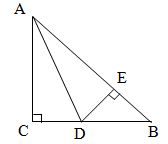(1)、已知CD=4cm，求AC的长；

(2)、求证：AB=AC+CD.

查看试题解析
22. 如图，方格中，每个小正方形的边长都是单位1，△ABC在平面直角坐标系中的位置如图.

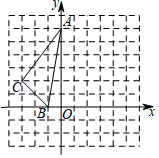(1)、①画出将△ABC向右平移2个单位得到△A₁B₁C₁.
②画出将△ABC绕点O顺时针方向旋转90°得到的△A₂B₂C₂.

(2)、在x轴上找一点P，满足点P到点C₁与C₂距离之和最小，并求出P点的坐标.

查看试题解析
23. 把一堆苹果分给几个孩子，如果每人分3个，那么多8个。如果前面每人分5个，那么最后一人得到的苹果不足3个，问有几个孩子？有多少个苹果？

查看试题解析
24. 某蓝莓种植生产基地产销两旺，采摘的蓝莓部分加工销售，部分直接销售，且当天都能销售完，直接销售是40元/斤，加工销售是130元/斤（不计损耗）．已知基地雇佣20名工人，每名工人只能参与采摘和加工中的一项工作，每人每天可以采摘70斤或加工35斤，设安排x名工人采摘蓝莓，剩下的工人加工蓝莓．

(1)、若基地一天的总销售收入为y元，求y与x的函数关系式；

(2)、试求如何分配工人，才能使一天的销售收入最大？并求出最大值．

查看试题解析
25. 四边形ABCD是正方形，△ADF旋转一定角度后得到△ABE，如图所示，如果AF＝5，AB＝9，求：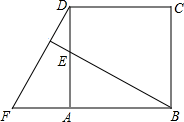

(1)、指出旋转中心和旋转角度；

(2)、求DE的长度；

(3)、BE与DF的位置关系如何？

查看试题解析
26. 已知：如图， $△ A B C$ 是边长为3cm的等边三角形，动点P、Q同时从A、B两点出发，分别沿AB、BC方向匀速移动，它们的速度都是 $1 c m / s$ ，当点P到达点B时，P、Q两点停止运动，设点P的运动时间 $t (s)$ ，解答下列各问题：

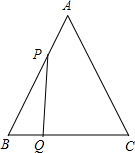(1)、经过 $\frac{2}{5}$ 秒时，求 $△ P B Q$ 的面积；

(2)、当t为何值时， $△ P B Q$ 是直角三角形？

(3)、是否存在某一时刻t，使四边形APQC的面积是 $△ A B C$ 面积的三分之二？如果存在，求出t的值；不存在请说明理由.

查看试题解析