江苏省无锡市2020届九年级下学期数学第一次月考试卷

试卷更新日期：2020-04-20 类型：月考试卷

进入出卷网下载

一、单选题

1. 4的平方根是（）

A、 ±2 B、2 C、﹣2 D、16

查看试题解析
2. 中国的陆地面积和领水面积共约9970000km² ， 9970000这个数用科学记数法可表示为（）

A、9.97×10⁵ B、99.7×10⁵ C、9.97×10⁶ D、0.997×10⁷

查看试题解析
3. 如图是由棱长为1的正方体搭成的某几何体三视图，则图中棱长为1的正方体的个数是（）

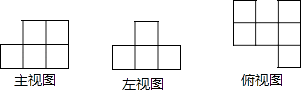A、9 B、8 C、7 D、6

查看试题解析

4. 在一次中学生田径运动会上，参加跳远的

15

名运动员的成绩如下表所示:

成绩（米）	$4.50$	$4.60$	$4.65$	$4.70$	$4.75$	$4.80$
人数	$2$	$3$	$2$	$3$	$4$	$1$

则这 $15$ 名运动员成绩的中位数、众数分别是（）

A、

4.65, 4.70

B、

4.65, 4.75

C、

4.70, 4.70

， D、

4.70, 4.75

查看试题解析

5. 函数y＝﹣x²﹣4x﹣3图象顶点坐标是（）

A、(2，﹣1) B、(﹣2，1) C、(﹣2，﹣1) D、(2，1)

查看试题解析
6. 下列命题中，是真命题的是（）

A、四条边相等的四边形是矩形 B、对角线互相平分的四边形是矩形 C、四个角相等的四边形是矩形 D、对角线相等的四边形是矩形

查看试题解析
7. 直角梯形ABCD如图放置，AB、CD为水平线，BC⊥AB，如果∠BCA＝67°，从低处A处看高处C处，那么点C在点A的（）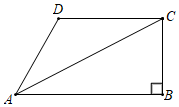

A、俯角67°方向 B、俯角23°方向 C、仰角67°方向 D、仰角23°方向

查看试题解析
8. 已知抛物线y＝ax²+3x+c（a，c为常数，且a≠0）经过点（﹣1，﹣1），（0，3），有下列结论：①ac＜0；②当x＞1时，y的值随x值的增大而减小；③3是方程ax²+2x+c＝0的一个根；④当﹣1＜x＜3时，ax²+2x+c＞0其中正确结论的个数是（）

A、1 B、2 C、3 D、4

查看试题解析
9. 如图，在平面直角坐标系中，A（-3，1），以点O为直角顶点作等腰直角三角形AOB，双曲线 $y_{1} = \frac{k_{1}}{x}$ 在第一象限内的图象经过点B，设直线AB的解析式为 $y_{2} = k_{2} x - b$ ，当 $y_{1} > y_{2}$ 时，x的取值范围是（）

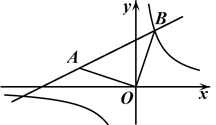A、-5＜x＜1 B、0＜x＜1或x＜-5 C、-6＜x＜1 D、0＜x＜1或x＜-6

查看试题解析
10. 如图，平面直角坐标系xOy中，点A的坐标为（9，6），AB⊥y轴，垂足为B，点P从原点O出发向x轴正方向运动，同时，点Q从点A出发向点B运动，当点Q到达点B时，点P、Q同时停止运动，若点P与点Q的速度之比为1：2，则下列说法正确的是（）

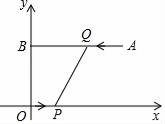A、线段PQ始终经过点（2，3） B、线段PQ始终经过点（3，2） C、线段PQ始终经过点（2，2） D、线段PQ不可能始终经过某一定点

查看试题解析

二、填空题

11. 若代数式 $- a^{m} b^{4}$ 和 $3 a b^{n}$ 是同类项，则 $m + n =$ .

查看试题解析
12. 若 $a^{2} - 3 b = 6$ ，则 $2022 + b - \frac{1}{3} a^{2}$ =.

查看试题解析
13. 分解因式：2m²-8= ．

查看试题解析
14. 若代数式 $\frac{x^{2} - 16}{2 x - 8}$ 的值等于 0，则 x＝ .

查看试题解析
15. 一个扇形的圆心角为135°，弧长为3πcm，则此扇形的面积是cm².

查看试题解析
16. 已知点 $P$ 是线段 $M N$ 的黄金分割点， $M P > N P$ ，且 $MP = (\sqrt{5} - 1) cm$ ，则 $M N$ 等于 $cm$ .

查看试题解析
17. 如图，在⊙O中，B，P，A，C是圆上的点， $\overset{⌢}{P B} = \overset{⌢}{P C}$ ， PD⊥CD，CD交⊙O于A，若AC=AD，PD = $\frac{4}{3}$ ，sin∠PAD = $\frac{4}{5}$ ，则△PAB的面积为.

查看试题解析
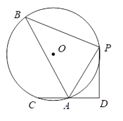18. 平面直角坐标系内，A(-1，0)，B(1，0)，C(4，﹣3)，P 在以 C 为圆心 1 为半径的圆上运动，连接 PA，PB，则 $P A^{2} + P B^{2}$ 的最小值是 .

查看试题解析

三、解答题

19. 计算

(1)、2^﹣¹+|1﹣ $\sqrt{8}$ |+（ $\sqrt{3}$ ﹣2）⁰﹣cos60°

(2)、（2﹣ $\frac{x - 1}{x + 1}$ ）÷ $\frac{x^{2} + 6 x + 9}{x^{2} - 1}$

查看试题解析
20.

(1)、解方程x²﹣2x﹣1=0

(2)、解不等式组： ${\begin{array}{l} 3 x - 5 ⩽ 1 ① \\ \frac{13 - x}{3} < 4 x ② \end{array}$

查看试题解析

21. 为践行习总书记提出的“绿水青山就是金山银山”重要思想，我市举办了 “重庆市第五届生态文明知识竞赛”.某校从七、八年级中各随机抽取20名同学的竞赛成绩(百分制)进行整理分析(成绩得分用

x

表示，共分成五组：(A.

75 \leq x < 80

80 \leq x < 85

， C.

85 \leq x < 90

， D.

90 \leq x < 95

， E.

95 \leq x \leq 100

)，绘制了如下不完整的统计图表：

年级	平均数	中位数	众数	满分率
七年级	91	a	b	25%
八年级	93	96	98	20%

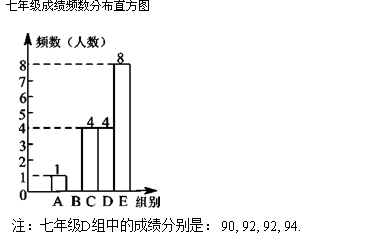
根据以上信息，解答下列问题：

(1)、补全频数分布直方图，并写出上表中a， b的值：a= ， b=；

(2)、七年级小明的成绩为93分，八年级小白的成绩为95分，哪位同学的成绩在各自年级抽取的同学中排名更靠前，请说明理由；

(3)、七年级共有400人，估计该年级此次竞赛成绩高于平均分91分的有多少人.

查看试题解析

22. 某市某幼儿园“六一”期间举行亲子游戏，主持人请三位家长分别带自己的孩子参加游戏。主持人准备把家长和孩子重新组合完成游戏，A、B、C分别表示三位家长，他们的孩子分别对应的是a、b、c．

(1)、若主持人分别从三位家长和三位孩子中各选一人参加游戏，恰好是A、a的概率是多少（直接写出答案）?

(2)、若主持人先从三位家长中任选两人为一组，再从孩子中任选两人为一组，四人共同参加游戏，恰好是两对家庭成员的概率是多少。（画出树状图或列表）

查看试题解析
23. 如图1是超市的手推车，如图2是其侧面示意图，已知前后车轮半径均为5 cm，两个车轮的圆心的连线AB与地面平行，测得支架AC＝BC＝60cm，AC、CD所在直线与地面的夹角分别为30°、60°，CD＝50cm.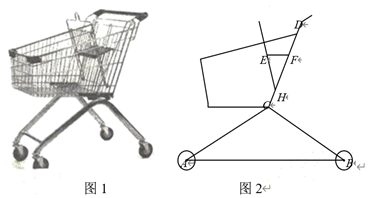

(1)、求扶手前端D到地面的距离；

(2)、手推车内装有简易宝宝椅，EF为小坐板，打开后，椅子的支点H到点C的距离为10 cm，DF＝20cm，EF∥AB，∠EHD＝45°，求坐板EF的宽度.（本题答案均保留根号）

查看试题解析
24. 现代互联网技术的广泛应用，催生了快递行业的高速发展，据调查，长沙某家小型“大学生自主创业”的快递公司，今年三月份与五月份完成投递总件数分别为10万件和14.4万件，现假定该公司每月投递总件数的增长率相同.

(1)、求该快递公司投递总件数的月平均增长率；

(2)、如果平均每人每月最多可投0.5万件，那么该公司现有的29名快递投递员能否完成今年6月份的快递投递任务？如果不能，请问需要至少增加几名业务员？

查看试题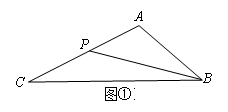解析
25. 如图

(1)、如图①，在△ABC中，AB＝m，AC＝n（n＞m），点P在边AC上.当AP＝时，△APB∽△ABC；

(2)、如图②，已知△DEF（DE＞DF），请用直尺和圆规在直线DF上求作一点Q，使DE是线段DF和DQ的比例项.（保留作图痕迹，不写作法）

查看试题解析
26. 如图，已知AB是⊙O的直径，过O点作OP⊥AB，交弦AC于点D，交⊙O于点E，且使∠PCA=∠ABC．

(1)、求证：PC是⊙O的切线；

(2)、若∠P=60°，PC=2，求PE的长．

查看试题解析
27. 如图，A、B两点的坐标分别是（8，0）、（0，6），点P由点B出发沿BA方向向点A作匀速直线运动，速度为每秒3个单位长度，点Q由A出发沿AO（O为坐标原点）方向向点O作匀速直线运动，速度为每秒2个单位长度，连接PQ，若设运动时间为t（0＜t＜ $\frac{10}{3}$ ）秒.解答如下问题：

(1)、当t为何值时，PQ∥BO？

(2)、设△AQP的面积为S，
①求S与t之间的函数关系式，并求出S的最大值；

②若我们规定：点P、Q的坐标分别为（x₁ ， y₁），（x₂ ， y₂），则新坐标（x₂﹣x₁ ， y₂﹣y₁）称为“向量PQ”的坐标.当S取最大值时，求“向量PQ”的坐标.

查看试题解析
28. 如图，抛物线 $y = a x^{2} + (4 a - 1) x - 4$ 与 x 轴交于点 A、B，与 y 轴交于点 C，且 OC＝2OB，点 D 为线段 OB 上一动点(不与点 B 重合)，过点 D 作矩形 DEFH，点 H、F 在抛物线上，点 E 在 x 轴上.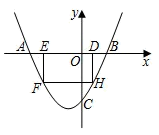

(1)、求抛物线的解析式；

(2)、当矩形 DEFH 的周长最大时，求矩形 DEFH 的面积；

(3)、在（2）的条件下，矩形 DEFH 不动，将抛物线沿着 x 轴向左平移 m 个单位，抛物线与矩形 DEFH的边交于点 M、N，连接 M、N.若 MN 恰好平分矩形 DEFH 的面积，求 m 的值.

查看试题解析